Discrete-Time Signal Representation

# OVERVIEW OF THE FIFTH MAIN CHAPTER #

A prerequisite for the system-theoretical investigation of digital systems or for their computer simulation is a suitable discrete-time signal description. This chapter clarifies the mathematical transition from time-continuous to time-discrete signals, starting from Fourier Transform and Its Inverse .

The chapter includes in detail:

the time and frequency domain representation of discrete-time signals,
the sampling theorem, which must be strictly observed in time discretization,
the reconstruction of the analog signal from the time-discrete representation,
the Discrete Fourier Transform (DFT) and its inverse (IDFT),
the possibilities of error when applying DFT and IDFT,
the application of spectral analysis to the improvement of metrological procedures, and.
the FFT algorithm particularly suitable for computer implementation.

For more information on the subject, as well as tasks, simulations, and programming exercises, see

Chapter 7: Discrete Fourier Transform, program dft,
Chapter 8: Spectral Analysis, program stp, and
Chapter 12: Pulse code modulation, program pcm

of the laboratory course „Simulation Methods in Communications Engineering”. This (former) LNT course at the TU Munich is based on

the teaching software package LNTsim ⇒ link refers to the ZIP version of the program,
the Lab Instruction - Part A ⇒ link refers to the PDF version; Chapter 7: page 119-144, Chapter 8: page 145-164, and
the Lab Instruction - Part B ⇒ link refers to the PDF version; Chapter 12: page 271-294.

Principle and Motivation

Many message signals are analog and thus simultaneously time-continuous and continuous in value. If such an analog signal is to be transmitted by means of a digital system, the following preprocessing steps are required:

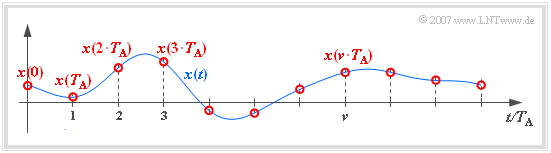
the sampling of the message signal $x(t)$ , which is expediently - but not necessarily - performed at equidistant times ⇒ time discretization,
the quantization of the samples, so as to limit the number $M$ of possible values to a finite value ⇒ value discretization.

Quantization is not discussed in detail until the chapter Pulse Code Modulation of the book "Modulation Methods".

On Time Discretization of the Time-Continuous Signal

$x(t)$

In the following, we use the following nomenclature to describe the sampling:

let the continuous-time signal be $x(t)$ .
Let the time-discretized signal sampled at equidistant intervals $T_{\rm A}$ be $x_{\rm A}(t)$ .
outside the sampling time points $\nu \cdot T_{\rm A}$ always holds $x_{\rm A}(t) = 0$ .
The iterating variable $\nu$ be an integer: $\nu \in \mathbb{Z} = \{\hspace{0.05cm} \text{...}\hspace{0.05cm} , –3, –2, –1, \hspace{0.2cm}0, +1, +2, +3, \text{...} \hspace{0.05cm}\}$ .
In contrast, at the equidistant sampling times with the constant $K$ , the result is:

$x_{\rm A}(\nu \cdot T_{\rm A}) = K \cdot x(\nu \cdot T_{\rm A})\hspace{0.05cm}.$

The constant depends on the type of time discretization. For the above sketch $K = 1$ holds.

Time Domain Representation

$\text{Definition:}$ Throughout $\rm LNTwww$ , the sampling shall be understood as the multiplication of the time-continuous signal $x(t)$ by the Dirac pulse $p_{\delta}(t)$ :

$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.05cm}.$

AIt should be noted that other forms of description are found in the literature. However, to the authors, the form chosen here appears to be the most appropriate in terms of spectral representation and derivation of the Discrete Fourier Transform (DFT).

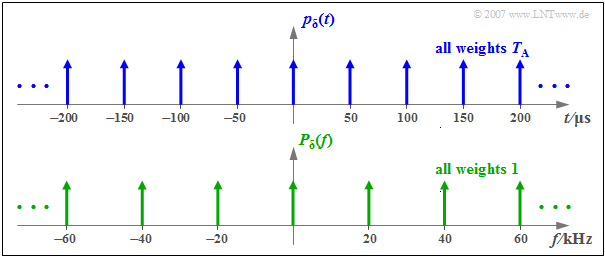
$\text{Definition:}$ The Dirac comb (in the time domain) consists of infinitely many Dirac pulses, each equally spaced $T_{\rm A}$ and all with equal pulse weight $T_{\rm A}$ :

$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$

Based on this definition, the sampled signal has the following properties:

The sampled signal at the considered time $(\nu \cdot T_{\rm A})$ is equal $T_{\rm A} \cdot x(\nu \cdot T_{\rm A}) - \delta (0)$ .
Since the Dirac function $\delta (t)$ is infinite at time $t = 0$ actually all signal values $x_{\rm A}(\nu \cdot T_{\rm A})$ are also infinite.
Thus, the factor $K$ introduced on the last page is actually infinite as well.
Two samples $x_{\rm A}(\nu_1 \cdot T_{\rm A})$ and $x_{\rm A}(\nu_2 \cdot T_{\rm A})$ however, differ in the same proportion as the signal values $x(\nu_1 \cdot T_{\rm A})$ and $x(\nu_2 \cdot T_{\rm A})$ .
The samples of $x(t)$ appear in the momentum weights of the Dirac functions:

$x_{\rm A}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$

The additional multiplication by $T_{\rm A}$ is necessary so that $x(t)$ and $x_{\rm A}(t)$ have the same unit. Note here that $\delta (t)$ itself has the unit "1/s".

The following pages will show that these equations, which take some getting used to, do lead to reasonable results, if they are applied consistently.

Dirac Comb in Time and Frequency Domain

$\text{Theorem:}$ Developing the Dirac comb into a Fourier Series and transforming it into the frequency domain using the Shift Theorem gives the following correspondence:

$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} P_{\delta}(f) = \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} ).$

Here $f_{\rm A} = 1/T_{\rm A}$ gives the distance between two adjacent dirac lines in the frequency domain.

$\text{Proof:}$ The derivation of the spectral function given here $P_{\delta}(f)$ is done in several steps:

(1) Since $p_{\delta}(t)$ is periodic with the constant distance $T_{\rm A}$ between two dirac lines, the [[[Signal_Representation/Fourier_Series#Komplexe_Fourierreihe|complex Fourier Series]] can be applied:

$p_{\delta}(t) = \sum_{\mu = - \infty }^{+\infty} D_{\mu} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot 2 \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}t/T_{\rm A} } \hspace{0.3cm}{\rm mit}\hspace{0.3cm} D_{\mu} = \frac{1}{T_{\rm A} } \cdot \int_{-T_{\rm A}/2 }^{+T_{\rm A}/2}p_{\delta}(t) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm} \cdot \hspace{0.05cm}t/T_{\rm A} }\hspace{0.1cm} {\rm d}t\hspace{0.05cm}.$

(2) In the range from $-T_{\rm A}/2$ to $+T_{\rm A}/2$ holds for the Dirac comb in the time domain: $p_{\delta}(t) = T_{\rm A} \cdot \delta(t)$ . Thus one can write for the complex Fourier coefficients:

$D_{\mu} = \int_{-T_{\rm A}/2 }^{+T_{\rm A}/2}{\delta}(t) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm} \cdot \hspace{0.05cm}t/T_{\rm A} }\hspace{0.1cm} {\rm d}t\hspace{0.05cm}.$

(3) Considering that for $t \neq 0$ the Dirac momentum is zero and for $t = 0$ the complex angular factor is equal to $1$ , it holds further:

$D_{\mu} = \int_{- T_{\rm A}/2 }^{+T_{\rm A}/2}{\delta}(t) \hspace{0.1cm} {\rm d}t = 1\hspace{0.5cm}{\Rightarrow}\hspace{0.5cm} p_{\delta}(t) = \sum_{\mu = - \infty }^{+\infty} {\rm e}^{ {\rm j} \hspace{0.05cm} \cdot 2 \hspace{0.05cm} \pi \cdot \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}t/T_{\rm A} }\hspace{0.05cm}.$

(4) The shifting theorem in the frequency domain is $f_{\rm A} = 1/T_{\rm A}$ :

${\rm e}^{ {\rm j} \hspace{0.05cm} \hspace{0.05cm} \cdot 2 \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm} f_{\rm A}\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} \delta (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$

(5) If you apply the result to each individual summand, you finally get:

$P_{\delta}(f) = \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$

q.e.d.

The result states:

The Dirac comb $p_{\delta}(t)$ in the time domain consists of infinitely many Dirac impulses, each at the same distance $T_{\rm A}$ and all with the same pulse weight $T_{\rm A}$ .
The Fourier transform of $p_{\delta}(t)$ again gives a Dirac comb, but now in the frequency range ⇒ $P_{\delta}(f)$ .
$P_{\delta}(f)$ also consists of infinitely many Dirac pulses, but now in the respective distance $f_{\rm A} = 1/T_{\rm A}$ and all with momentum weight $1$ .
The distances of the diraclines in the time and frequency domain representation thus follow the reciprocity theorem:

$T_{\rm A} \cdot f_{\rm A} = 1 \hspace{0.05cm}.$

Dirac Comb in the Time- and Frequency Domain

$\text{Example 1:}$ The graph illustrates the above statements for

$T_{\rm A} = 50\,{\rm µs}$ ,
$f_{\rm A} = 1/T_{\rm A} = 20\,\text{kHz}$ .

One can also see from this sketch the different momentum weights of $p_{\delta}(t)$ and $P_{\delta}(f)$ .

Frequency Domain Representation

The spectrum of the sampled signal $x_{\rm A}(t)$ is obtained by applying the convolution theorem in the frequency domain.This states that multiplication in the time domain corresponds to convolution in the spectral domain:

$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X_{\rm A}(f) = X(f) \star P_{\delta}(f)\hspace{0.05cm}.$

From the spectrum $X(f)$ by convolution with the diracline shifted by $\mu \cdot f_{\rm A}$ we get:

$X(f) \star \delta (f- \mu \cdot f_{\rm A} )= X (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$

Applying this result to all diraclines of the Dirac pulse, we finally obtain:

$X_{\rm A}(f) = X(f) \star \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} ) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$

The sampling of the analogue time signal $x(t)$ at equidistant intervals $T_{\rm A}$ leads in the spectral domain to a periodic continuation of $X(f)$ with frequency spacing of $f_{\rm A} = 1/T_{\rm A}$ .

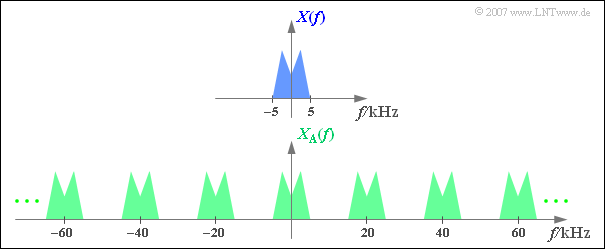
$\text{Example 2:}$ The upper graph shows (schematically!) the spectrum $X(f)$ of an analogue signal $x(t)$ , which includes frequencies up to $5 \text{ kHz}$ .

Spectrum of the Sampled Signal

Sampling the signal at the sampling rate $f_{\rm A}\,\text{ = 20 kHz}$ , i.e. at the respective distance $T_{\rm A}\, = {\rm 50 \, µs}$ we obtain the periodic spectrum $X_{\rm A}(f)$ sketched below.

Since the Dirac functions are infinitely narrow, the sampled signal $x_{\rm A}(t)$ also contains arbitrary high-frequency components.
Accordingly, the spectral function $X_{\rm A}(f)$ of the sampled signal is extended to infinity.

Signal Reconstruction

Signal sampling is not an end in itself in a digital transmission system; it must be reversed at some point. Consider, for example, the following system:

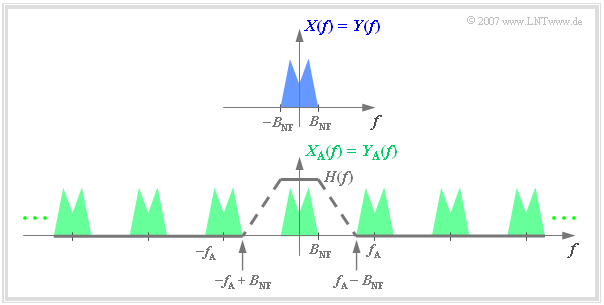
Sampling and Reconstruction of a Signal

The analogue signal $x(t)$ with bandwidth $B_{\rm NF}$ is sampled as described above.
At the output of an ideal transmission system, the likewise time-discrete signal $y_{\rm A}(t) = x_{\rm A}(t)$ is present.
The question now is how the block signal reconstruction is to be designed so that also $y(t) = x(t)$ applies.

The solution is relatively simple if one considers the spectral functions: One obtains from $Y_{\rm A}(f)$ the spectrum $Y(f) = X(f)$ by a low-pass with the Frequency Response $H(f)$ , which

Frequency Domain Representation of the Signal Reconstruction Process

passes the low frequencies unaltered:

$H(f) = 1 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \le B_{\rm NF}\hspace{0.05cm},$

suppresses the high frequencies completely:

$H(f) = 0 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \ge f_{\rm A} - B_{\rm NF}\hspace{0.05cm}.$

Further it can be seen from the graph that the frequency response $H(f)$ in the range of $B_{\rm NF}$ to $f_{\rm A}-B_{\rm NF}$ can be arbitrarily shaped,

for example, linearly sloping (dashed line)
or also rectangular,

as long as both of the above conditions are met.

The Sampling Theorem

The complete reconstruction of the analogue signal $y(t)$ from the sampled signal $y_{\rm A}(t) = x_{\rm A}(t)$ is only possible if the sampling rate $f_{\rm A}$ corresponding to the bandwidth $B_{\rm NF}$ of the message signal has been chosen correctly.

From the graph of the last page , it can be seen that the following condition must be fulfilled:

$f_{\rm A} - B_{\rm NF} > B_{\rm NF} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm A} > 2 \cdot B_{\rm NF}\hspace{0.05cm}.$

$\text{Sampling Theorem:}$ If an analogue signal $x(t)$ has spectral components in the range $\vert f \vert < B_{\rm NF}$ , it can only be completely reconstructed from its sampled signal if the sampling rate is sufficiently large:

$f_{\rm A} ≥ 2 \cdot B_{\rm NF}.$

Accordingly, the following must apply to the distance between two samples:

$T_{\rm A} \le \frac{1}{ 2 \cdot B_{\rm NF} }\hspace{0.05cm}.$

If the largest possible value ⇒ $T_{\rm A} = 1/(2B_{\rm NF})$ is used for sampling,

then, in order to reconstruct the analogue signal from its sampled values,
one must use an ideal, rectangular low-pass filter with cut-off frequency $f_{\rm G} = f_{\rm A}/2 = 1/(2T_{\rm A})$ .

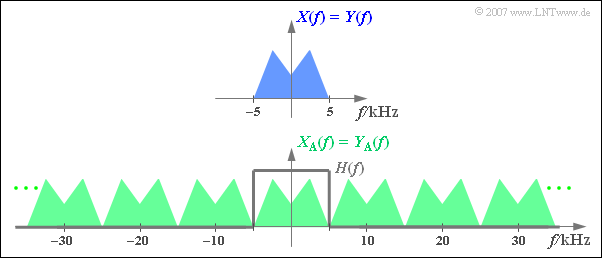
$\text{Example 3:}$ The graph above shows the spectrum $\pm\text{ 5 kHz}$ of an analogue signal limited to $X(f)$ below the spectrum $X_{\rm A}(f)$ of the signal sampled at distance $T_{\rm A} =\,\text{ 100 µs}$ ⇒ $f_{\rm A}=\,\text{ 10 kHz}$ .

Sampling Theorem in the Frequency Domain

Additionally drawn is the frequency response $H(f)$ of the low-pass filter for signal reconstruction, whose cut-off frequency must be $f_{\rm G} = f_{\rm A}/2 = 5\,\text{ kHz}$ .

With any other $f_{\rm G}$ value, the result would be $Y(f) \neq X(f)$ .
For $f_{\rm G} < 5\,\text{ kHz}$ the upper $X(f)$ portions are missing.
At $f_{\rm G} > 5\,\text{ kHz}$ there are unwanted spectral components in $Y(f)$ due to convolution operations.

If the sampling at the transmitter had been done with a sampling rate $f_{\rm A} < 10\,\text{ kHz}$ ⇒ $T_{\rm A} >100 \,{\rm µ s}$ , the analogue signal $y(t) = x(t)$ would not be reconstructible from the samples $y_{\rm A}(t)$ in any case.

Note: There is an interactive applet on the topic covered here: Sampling of Analogue Signals and Signal Reconstruction

Exercises For the Chapter

Exercise 5.1: Sampling Theorem

Exercise 5.1Z: Sampling of Harmonic Oscillations