Exercise 2.6: Complex Fourier Series

• Return to book

Verschiedene periodische Dreiecksignale

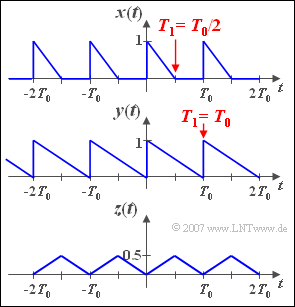
We consider the signal  $x(t)$, defined by the two parameters  $T_0$  and  $T_1$  where  $T_1 \leq T_0$  should always apply. For the complex Fourier coefficients

$$D_n=\frac{1}{T_0} \cdot \int_0^{T_0}x(t)\cdot\rm e^{-\rm j\it n\omega_0t}\,{\rm d} \it t$$

of this signal are obtained after mathematical transformations:

$$D_n=\frac{T_0/T_1} {(2\pi n)^2} \cdot \bigg(1-{\rm e}^{-{\rm j} 2\pi nT_1/T_0}\bigg)-\frac{\rm j}{2\pi n}.$$

• The parameter set dealt with in subtasks  (1)  and  (3)    $($with $T_1 = T_0/2)$  is represented as the signal  $x(t)$ .
• For  $T_1 = T_0$  ⇒   subtask  (2)  the function  $y(t)$ results.
• In subtask  (4)  the signal  $z(t)$  is considered. Its Fourier coefficients are:

$$A_0=1/4,\hspace{1cm} A_n=\left\{ \begin{array}{cl} {\frac{\displaystyle-2}{\displaystyle(\pi n)^2}} & {\rm f\ddot{u}r\; geradzahliges\; \it n \rm ,} \\ 0 & {\rm f\ddot{u}r\; ungeradzahliges\; \it n,} \end{array}\right. $$

$$B_n=0\; \;\; \rm{ f\ddot{u}r\; alle\; \it n.}$$

Hints:

• This exercise refers to the page  Complex Fourier Series.

Questions

1

Calculate the coefficient  $D_0$  and show that it is always real. What value results for  $T_1 = T_0/2$, i.e. for the signal  $x(t)$?

$D_0^{(x)}\ = \ $

2

Calculate the complex Fourier coefficients  $D_n^{(y)}$  for  $n \neq 0$ for the special case   $T_1 = T_0$  corresponding to the signal  $y(t)$ .
What are the coefficients  $A_n^{(y)}$  and  $B_n^{(y)}$, especially for  $n = 1$?

$A_1^{(y)}\ = \ $

$B_1^{(y)}\ = \ $

3

Now calculate the coefficients  $A_n^{(x)}$  and  $B_n^{(x)}$  for the signal  $x(t)$  with  $T_1 = T_0/2$  for  $n \neq 0$. What are the values for  $A_1^{(x)}$  and  $B_1^{(x)}$?

$A_1^{(x)}\ = \ $

$B_1^{(x)}\ = \ $

4

Which of the following statements are true regarding  $x(t)$,  $y(t)$  and  $z(t)$ ?

	It is true that  $x(t) = y(t) + z(t)$.
	It is true that  $x(t) = y(t) - z(t)$.
	The cosine coefficients  $A_n$  of  $x(t)$  und  $z(t)$  are identical.
	The cosine coefficients  $A_n$  of  $x(t)$  und  $z(t)$  are equal in magnitude.
	The sine coefficients  $B_n$  of  $y(t)$  und  $z(t)$  are identical.

Solution

Solution

(1)  Mit dem Eulerschen Satz ist der komplexe Fourierkoeffizient  $D_n$  wie folgt darstellbar:

$${\rm Re} [D_n] =\frac{T_0/T_1}{(2\pi n)^2}\cdot(1-\cos(2\pi nT_1/T_0)),$$

$${\rm Im}[D_n] =\frac{T_0/T_1}{(2\pi n)^2} \cdot \sin(2\pi nT_1/T_0)-\frac{1}{2\pi n}.$$

• Mit der für kleine  $\alpha$-Werte gültigen Näherung  $\text{sin}(\alpha ) \approx \alpha$  erhält man für den Imaginärteil:

$${\rm Im}[D_n] =\frac{T_0/T_1}{(2\pi n)^2}\cdot(2\pi nT_1/T_0)-\frac{1}{2\pi n}=0.$$

• Für den Realteil erhält man mit  $\text{cos}(\alpha) \approx 1 – \alpha^{2}/2$:

$${\rm Re}[D_n] =\frac{T_0/T_1}{(2\pi n)^2}\frac{(2\pi nT_1/T_0)^2}{2}=\frac{T_1/T_0}{2}.$$

• Für  $T_1 = T_0/2$  folgt daraus der Gleichsignalkoeffizient  $D_0^{(x)} \hspace{0.1cm}\underline{= 0.25}$.
• Mit  $T_1 = T_0$  ergibt sich  $D_0^{(y)} = 0.5$.
• Ein Vergleich mit den Signalen  $x(t)$  und  $y(t)$  auf der Angabenseite zeigen die Richtigkeit dieser Ergebnisse.

(2)  Es wird nun  $n \neq 0$  vorausgesetzt. Mit  $T_1 = T_0$  erhält man für den Realteil wegen  $\text{cos}(2\pi n) = 1$:

$${\rm Re}[D_n^{(y)}] =\frac{1}{(2\pi n)^2}\cdot(1-\cos(2\pi n))=0.$$

• Der Imagnärteil lautet:

$${\rm Im}[D_n^{(y)}] =\frac{1}{(2\pi n)^2}\cdot(\sin(2\pi n))-\frac{1}{2\pi n}.$$

• Wegen  $\text{sin}(2\pi n) = 0$  folgt daraus   ${\rm Im}[D_n] =-{1}/({2\pi n}).$ Somit ist

$$D_n^{(y)}=\frac{-\rm j}{2\pi n}={1}/{2} \cdot (A_n- {\rm j} \cdot B_n).$$

• Der Koeffizientenvergleich liefert  $A_n^{(y)} = 0$  und  $B_n^{(y)} = 1/(\pi n)$. Insbesondere sind  $A_1^{(y)} \hspace{0.1cm}\underline{= 0}$  und  $B_1^{(y)}\hspace{0.1cm}\underline{ \approx 0.318}$.

• Wie zu erwarten war, gilt stets $B_{-n}^{(y)} = -B_n^{(y)}$.

(3)  Aus der in der Teilaufgabe  (1)  berechneten allgemeinen Gleichung folgt mit  $T_1/T_0 = 1/2$:

$$D_n^{(x)}=\frac{2}{(2\pi n)^2}(1-\cos(\pi n))+{\rm j}\cdot \left[\frac{2\sin(\pi n)}{(2\pi n)^2}-\frac{1}{(2\pi n)}\right].$$

• Daraus erhält man die Cosinuskoeffizienten

$$A_n^{(x)}={2}\cdot{\rm Re}[D_n] =\left\{ \begin{array}{cl} {\frac{\displaystyle 2}{\displaystyle(\pi n)^2}} & {\rm f\ddot{u}r\; ungeradzahliges\; \it n ,} \\ 0 & {\rm f\ddot{u}r\; geradzahliges\;\it n.} \end{array}\right. $$

• Die Sinuskoeffizienten lauten:

$$B_n^{(x)}=-2\cdot{\rm Im}[D_n] =\frac{1}{\pi n}.$$

• Hierbei ist berücksichtigt, dass für alle ganzzahligen Werte von  $n$  die Funktion  $\text{sin}(n\pi ) = 0$  ist. Die jeweils ersten reellen Koeffizienten lauten

$$A_1^{(x)} = 2/\pi^{2} \hspace{0.1cm}\underline{\approx 0.203},$$

$$B_1 = 1/\pi \hspace{0.1cm}\underline{\approx 0.318}.$$

(4)  Richtig sind die Lösungsvorschläge 2, 4 und 5:

• Das Signal  $x(t)$  ist gleich der Differenz zwischen  $y(t)$  und  $z(t)$. Da  $z(t)$  eine gerade und  $y(t)$  eine ungerade Funktion ist, werden die Cosinuskoeffizienten  $A_n$  allein durch die Koeffizienten des Signals  $z(t)$  bestimmt, allerdings mit negativen Vorzeichen.
• Die Sinuskoeffizienten $B_n$ stimmen vollständig mit denen von  $y(t)$  überein.
• Der Gleichsignalanteil von  $x(t)$  ergibt sich aus der Differenz der beiden Gleichanteile von  $y(t)$  und  $z(t)$:  

$$A_0 = 0.5 - 0.25 = 0.25.$$