Two-Dimensional Gaussian Random Variables

Wahrscheinlichkeitsdichte- und Verteilungsfunktion

Alle bisherigen Aussagen des vierten Hauptkapitels "Zufallsgrößen mit statistischen Bindungen" gelten allgemein.

Für den Sonderfall Gaußscher Zufallsgrößen – der Name geht auf den Wissenschaftler Carl Friedrich Gauß zurück – können wir weiterhin vermerken:

Die Verbundwahrscheinlichkeitsdichtefunktion einer Gaußschen 2D-Zufallsgröße $(x, y)$ mit Mittelwerten $m_x = 0$ , $m_y = 0$ und Korrelationskoeffizienten $ρ_{xy}$ lautet:

$f_{xy}(x,y)=\frac{\rm 1}{\rm 2\it\pi \cdot \sigma_x \cdot \sigma_y \sqrt{\rm 1-\rho_{\it xy}^2}}\cdot\exp\Bigg[-\frac{\rm 1}{\rm 2 (1-\it\rho_{xy}^{\rm 2} {\rm)}}\cdot(\frac {\it x^{\rm 2}}{\sigma_x^{\rm 2}}+\frac {\it y^{\rm 2}}{\sigma_y^{\rm 2}}-\rm 2\it\rho_{xy}\cdot\frac{x \cdot y}{\sigma_x \cdot \sigma_y}\rm ) \rm \Bigg].$

Ersetzt man $x$ durch $(x - m_x)$ sowie $y$ durch $(y- m_y)$ , so ergibt sich die allgemeinere WDF einer zweidimensionalen Gaußschen Zufallsgröße mit Mittelwert.
Die beiden Randwahrscheinlichkeitsdichtefunktionen $f_{x}(x)$ und $f_{y}(y)$ einer Gaußschen 2D-Zufallsgröße sind ebenfalls gaußförmig mit den Streuungen $σ_x$ bzw. $σ_y$ .
Bei unkorrelierten Komponenten $x$ und $y$ muss in obiger Gleichung $ρ_{xy} = 0$ eingesetzt werden, und man erhält dann das Ergebnis:

$f_{xy}(x,y)=\frac{1}{\sqrt{2\pi}\cdot\sigma_{x}} \cdot\rm e^{-\it {x^{\rm 2}}\hspace{-0.08cm}/{\rm (}{\rm 2\it\sigma_{x}^{\rm 2}} {\rm )}} \cdot\frac{1}{\sqrt{2\pi}\cdot\sigma_{\it y}}\cdot e^{-\it {y^{\rm 2}}\hspace{-0.08cm}/{\rm (}{\rm 2\it\sigma_{y}^{\rm 2}} {\rm )}} = \it f_{x} \rm ( \it x \rm ) \cdot \it f_{y} \rm ( \it y \rm ) .$

$\text{Fazit:}$ Im Sonderfall einer 2D-Zufallsgröße mit Gaußscher WDF $f_{xy}(x, y)$ folgt aus der Unkorreliertheit auch direkt die statistische Unabhängigkeit:

$f_{xy}(x,y)= f_{x}(x) \cdot f_{y}(y) .$

Bitte beachten Sie:

Bei keiner anderen WDF kann aus der Unkorreliertheit auf die statistische Unabhängigkeit geschlossen werden.
Man kann aber stets ⇒ für jede beliebige 2D–WDF $f_{xy}(x, y)$ von der statistischen Unabhängigkeit auf die Unkorreliertheit schließen, weil:
Sind zwei Zufallsgrößen $x$ und $y$ völlig voneinander (statistisch) unabhängig, so gibt es zwischen ihnen natürlich auch keine linearen Abhängigkeiten
⇒ sie sind dann auch unkorreliert.

Gaußsche 2D-WDF und 2D-VTF

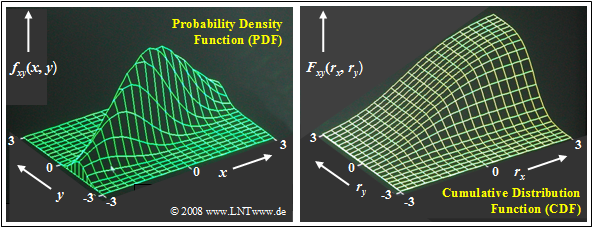
$\text{Beispiel 1:}$ Die beiden Grafiken zeigen

die Wahrscheinlichkeitsdichtefunktion (links) und
Verteilungsfunktion (rechts)

einer zweidimensionalen Gaußschen Zufallsgröße $(x, y)$ mit relativ starker positiver Korrelation der Einzelkomponenten: $ρ_{xy} = 0.8$ .

Wie bei den bisherigen Beispielen ist auch hier die 2D–Zufallsgröße in $x$ –Richtung weiter ausgedehnt als in $y$ –Richtung: $σ_x = 2 · σ_y$ .
Diese Darstellungen können wie folgt interpretiert werden:

Die WDF ist hier vergleichbar mit einem Bergkamm, der sich von links unten nach rechts oben erstreckt.
Das Maximum liegt bei $m_x = 0$ und $m_y = 0$ . Das bedeutet, dass die die 2D–Zufallsgröße mittelwertfrei ist.
Die 2D–VTF als das Integral in zwei Richtungen über die 2D–WDF steigt von links unten nach rechts oben von $0$ auf $1$ kontinuierlich an.

Das interaktive Applet WDF und VTF bei Gaußschen 2D-Zufallsgrößen erlaubt die Darstellung der zweidimensionalen Funktionen für beliebige Werte von $σ_x, \ σ_y$ und $ρ_{xy}$ .

Höhenlinien bei unkorrelierten Zufallsgrößen

rechts

Aus der Bedingungsgleichung $f_{xy}(x, y) = \rm const.$ können die Höhenlinien der WDF berechnet werden.

Sind die Komponenten $x$ und $y$ unkorreliert $(ρ_{xy} = 0)$ , so erhält man als Gleichung für die Höhenlinien:

$\frac{x^{\rm 2}}{\sigma_{x}^{\rm 2}}+\frac{y^{\rm 2}}{\sigma_{y}^{\rm 2}} =\rm const.$

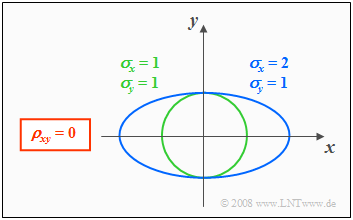
Die Höhenlinien beschreiben in diesem Fall folgende Figuren:

Kreise $($ falls $σ_x = σ_y$ , grüne Kurve $)$ , oder
Ellipsen $($ für $σ_x ≠ σ_y$ , blaue Kurve $)$ in Ausrichtung der beiden Achsen.

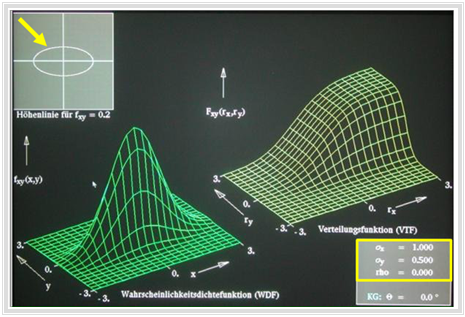
Bildschirmabzug des Lernvideos "Gaußsche 2D-Zufallsgrößen"

$\text{Beispiel 2:}$

Weitere Informationen zu dieser Thematik mit Signalbeispielen bietet der erste Teil "Gaußsche Zufallsgrößen ohne statistische Bindungen" des Lernvideos

Gaußsche 2D-Zufallsgrößen.

Die Grafik zeigt eine Momentaufnahme dieses Lernvideos.

Der zweite Teil behandelt "Gaußsche Zufallsgrößen mit statistischen Bindungen" gemäß dem folgenden Abschnitt.

Höhenlinien bei korrelierten Zufallsgrößen

Bei korrelierten Komponenten $(ρ_{xy} ≠ 0)$ sind die Höhenlinien der WDF stets elliptisch, also auch für den Sonderfall $σ_x = σ_y$ .

Hier lautet die Bestimmungsgleichung der WDF-Höhenlinien:

$f_{xy}(x, y) = {\rm const.} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \frac{x^{\rm 2} }{\sigma_{x}^{\rm 2}}+\frac{y^{\rm 2} }{\sigma_{y}^{\rm 2} }-{\rm 2}\cdot\rho_{xy}\cdot\frac{x\cdot y}{\sigma_x\cdot \sigma_y}={\rm const.}$

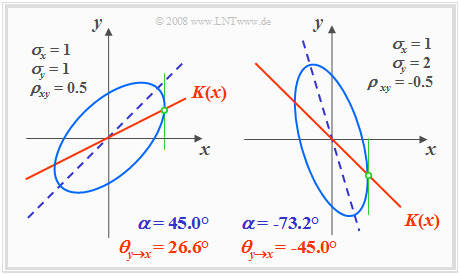
Die folgende Grafik zeigt in hellerem Blau zwei Höhenlinien für unterschiedliche Parametersätze, jeweils mit $ρ_{xy} ≠ 0$ .

Höhenlinien der 2D-WDF bei korrelierten Größen

Die Ellipsenhauptachse ist dunkelblau gestrichelt.
Die Korrelationsgerade $K(x)$ ist durchgehend rot eingezeichnet.

Anhand dieser Darstellung sind folgende Aussagen möglich:

Die Ellipsenform hängt außer vom Korrelationskoeffizienten $ρ_{xy}$ auch vom Verhältnis der beiden Streuungen $σ_x$ und $σ_y$ ab.
Der Neigungswinkel $α$ der Ellipsenhauptachse (gestrichelte Gerade) gegenüber der $x$ –Achse hängt ebenfalls von $σ_x$ , $σ_y$ und $ρ_{xy}$ ab:

$\alpha = {1}/{2} \cdot {\rm arctan } \ ( 2 \cdot \rho_{xy} \cdot \frac {\sigma_x \cdot \sigma_y}{\sigma_x^2 - \sigma_y^2}).$

Die (rote) Korrelationsgerade $y = K(x)$ einer Gaußschen 2D–Zufallsgröße liegt stets unterhalb der (blau gestrichelten) Ellipsenhauptachse.
$K(x)$ kann auch aus dem Schnittpunkt der Höhenlinien und ihrer vertikalen Tangenten geometrisch konstruiert werden, wie es in obigen Skizzen in grüner Farbe angedeutet ist.

Weitere Informationen zu dieser Thematik liefert das Lernvideo Gaußsche 2D-Zufallsgrößen:

Teil 1: Gaußsche Zufallsgrößen ohne statistische Bindungen,
Teil 2: Gaußsche Zufallsgrößen mit statistischen Bindungen.

Drehung des Koordinatensystems

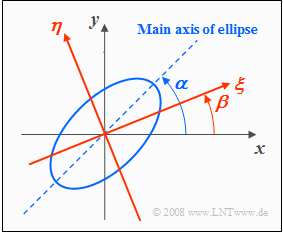
Bei manchen Aufgabenstellungen ist es vorteilhaft, das Koordinatensystem zu drehen, wie in der folgenden Grafik angedeutet:

rechts

Das $(ξ, η)$ -Koordinatensystem ist gegenüber dem ursprünglichen $(x, y)$ -System um den Winkel $β$ gedreht.
Dagegen bezeichnet $α$ den Winkel zwischen der Ellipsenhauptachse und der $x$ –Achse.

Zwischen den Koordinaten der beiden Bezugssysteme bestehen folgende Zusammenhänge:

$\xi = \hspace{0.4cm} \cos (\beta) \cdot x + \sin (\beta) \cdot y \hspace{0.55cm}{\rm bzw. }\hspace{0.5cm} x = \cos (\beta) \cdot \xi - \sin (\beta) \cdot \eta ,$

$\eta = - \sin (\beta) \cdot x + \cos (\beta) \cdot y \hspace{0.5cm}{\rm bzw. }\hspace{0.5cm} y = \sin (\beta) \cdot \xi + \cos (\beta) \cdot \eta .$

Ist $(x, y)$ eine Gaußsche 2D-Zufallsgröße, so ist die Zufallsgröße $(ξ, η)$ ebenfalls gaußverteilt.

Setzt man die obigen Gleichungen in die 2D-WDF $f_{xy}(x, y)$ ein und vergleicht die Koeffizienten, so erhält man folgende Bestimmungsgleichungen für $σ_x$ , $σ_y$ und $ρ_{xy}$ bzw. für $σ_ξ, σ_η$ und $ρ_{ξη}$ :

$\frac {1}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi^2} = \frac {1}{(1 - \rho_{xy}^2) } \left[ \frac {\cos^2 (\beta)}{\sigma_{x}^2 } + \frac {\sin^2 (\beta)}{\sigma_{y}^2 } - 2 \rho_{xy} \cdot \frac {\sin (\beta) \cdot \cos (\beta)}{\sigma_{x} \cdot \sigma_{y}}\right ] ,$

$\frac {1}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\eta^2} = \frac {1}{(1 - \rho_{xy}^2) } \left[ \frac {\sin^2 (\beta)}{\sigma_{x}^2 } + \frac {\cos^2 (\beta)}{\sigma_{y}^2 } + 2 \rho_{xy} \cdot \frac {\sin (\beta) \cdot \cos (\beta)}{\sigma_{x} \cdot \sigma_{y}}\right ] ,$

$\frac {\rho_{\xi \eta}}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi\cdot \sigma_\eta}= \frac {1}{(1 - \rho_{xy}^2) } \left[ \frac {\sin (\beta) \cdot \cos (\beta)}{\sigma_{x}^2 } - \frac {\sin (\beta) \cdot \cos (\beta)}{\sigma_{y}^2 } + \frac {\rho_{xy}}{\sigma_{x} \cdot \sigma_{y}} \cdot ( \cos^2( \beta) -\sin^2( \beta)) \right ] .$

Mit diesen drei Gleichungen können die jeweils drei Parameter der beiden Koordinatensysteme direkt umgerechnet werden, was allerdings nur in Sonderfällen ohne erheblichen Rechenaufwand möglich ist. Es folgt ein Beispiel mit vertretbarem Rechenaufwand.

$\text{Beispiel 3:}$ Wir betrachten eine Gaußsche 2D-WDF mit folgenden Eigenschaften:

Die Varianzen der beiden Komponenten sind gleich: $σ_x^2 = σ_y^2 = 1$ .
Der Korrelationskoeffizient zwischen $x$ und $y$ ist $ρ_{xy} = 0.5$ .
Der Winkel der Ellipsenhauptachse gegenüber der $x$ –Achse beträgt somit $α = 45^\circ$ .

Würde man das Koordinatensystem ebenfalls um $β =45^\circ$ drehen, so ergäbe sich wegen $σ_x = σ_y$ und wegen $\sin(β) = \cos(β) = 1/\sqrt{2}$ für den neuen Korrelationskoeffizienten $ρ_{ξη} = 0$ ⇒ unkorrelierte Komponenten.

Die beiden Streuungen – bezogen auf das neue Koordinatensystem – ergäben sich dann entsprechend den beiden ersten Gleichungen zu $σ_ξ = \sqrt{1.5}$ und $σ_η = \sqrt{0.5}$ .

Der obigen Skizze ist allerdings nicht $β = α$ zugrundegelegt, sondern $β = α/2$ .

Mit $σ_x = σ_y = 1$ , $ρ_{xy} = 0.5$ ,
sowie $α = 45^\circ$ , $\sin(β) · \cos(β) = \sin(2β)/2 = \sin(α)/2$ und
$\cos^2(β) - \sin^2(β) = \cos(2β)= \cos(α)$

kann das Gleichungssystem wie folgt dargestellt werden:

${\rm (I)}\hspace{0.8cm}\frac {1}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi^2} = \frac {4}{3} \left[ 1 - \frac {1}{2}\cdot {\sin (\alpha) }\right ] = 0.862 ,$

${\rm (II)}\hspace{0.68cm}\frac {1}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\eta^2} = \frac {4}{3} \left[ 1 + \frac {1}{2}\cdot {\sin (\alpha) }\right ] = 1.805 ,\hspace{0.28cm}\frac {\rm (I)}{\rm (II)}: \frac {\sigma_\eta}{\sigma_\xi} = \sqrt{\frac{0.862}{1.805} }= 0.691,$

${\rm (III)}\hspace{0.54cm}\frac {\rho_{\xi \eta} }{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi\cdot \sigma_\eta}= \frac {\rho_{\xi \eta} }{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi^2 \cdot 0.691}=\frac {2}{3}\cdot \cos( \alpha) = 0.471.$

Dividiert man nun die Gleichung $\rm (III)$ durch die Gleichung $\rm (I)$ , so erhält man:

$\frac {\rho_{\xi \eta} }{0.691}=\frac {0.471}{0.862}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}{\rho_{\xi \eta} }= 0.378.$

Die beiden weiteren Parameter des neuen Koordinatensystems ergeben sich nun zu $σ_ξ ≈ 1$ und $σ_η ≈ 0.7$ .