Exercise 1.3: Measured Step Response

Measured step response

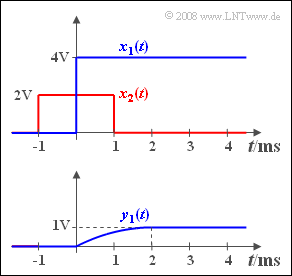
A step-shaped signal $$x_1(t) = 4\hspace{0.05cm} {\rm V} \cdot \gamma(t)$$ (blue curve) is applied to the input of a linear time-invariant (LTI) transmission system

with the frequency response $H(f)$
and the impulse response $h(t)$.

The measured output signal $y_1(t)$ then has the curve shown below.

With $T = 2 \,{\rm ms}$ this signal can be described in the range from $0$ to $T$ as follows:

$$y_1(t) = 2 \hspace{0.05cm}{\rm V} \cdot\big[ {t}/{T} - 0.5 \cdot ({t}/{T})^2\big].$$

From $t = T $ on $y_1(t)$ is constantly equal $1 \,{\rm V}$.

In the last subtask (5) the output signal $y_2(t)$ is to be determined if a symmetrical rectangular pulse $x_2(t)$ of duration $T = 2 \hspace{0.05cm} {\rm ms}$ is applied to the input (see red curve in the upper graph).

Please note:

The task belongs to the chapter System Description in Time Domain.
The rectangular pulse $x_2(t)$ can also be written as follows with $A = 2 \hspace{0.05cm} \text{V}$ :

$$x_2(t) = A \cdot \big [\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big ].$$

The frequency response $H(f)$ of the LTI system considered here can be taken from the exercise description of Exercise 3.8 in the book "Signal Representation”. However, the abscissa and ordinate parameters have to be adjusted accordingly.
For the solution of the problem on hand, though, $H(f)$ is not explicitly required.

Questions

	$H(f)$ describes an acausal system.
	$H(f)$ describes a causal system.
	$H(f)$ describes a low-pass filter.
	$H(f)$ describes a high-pass filter.

$H(f = 0) \ =\ $

$σ(t = \rm 1 \: ms) \ = \ $

$h(t = \rm 1 \: ms) \ =\ $

$\text {1/s}$

$h(t = \rm 2 \: ms) \ =\ $

$\text {1/s}$

$y_2(t = t_1) \ =\ $

$\text {V}$

$y_2(t = t_2) \ =\ $

$\text {V}$

$y_2(t = t_3) \ =\ $

$\text {V}$

$y_2(t = t_4) \ =\ $

$\text {V}$

Sample solution

Solution

(1) Richtig sind die Lösungsvorschläge 2 und 3:

Für das Ausgangssignal gilt $y_1(t)=0$, solange das Eingangssignal $x_1(t) = 0$ ist. Das bedeutet, dass hier ein kausales System vorliegt.
Zum gleichen Ergebnis hätte man allein durch die Aussage „das Ausgangssignal wurde gemessen” kommen können. Nur kausale Systeme sind realisierbar und nur bei realisierbaren Systemen kann etwas gemessen werden.
Das Eingangssignal $x_1(t)$ kann für sehr große Zeiten $(t \gg 0)$ als Gleichsignal interpretiert werden. Wäre $H(f)$ ein Hochpass, dann müsste $y_1(t)$ für $t → ∞$ gegen Null gehen. Das heißt: $H(f)$ stellt einen Tiefpass dar.

(2) Der Gleichsignalübertragungsfaktor kann aus $x_1(t)$ und $y_1(t)$ abgelesen werden, wenn der Einschwingvorgang abgeklungen ist:

$$H(f =0) = \frac{y_1(t \rightarrow \infty)}{x_1(t \rightarrow \infty)}= \frac{ {\rm 1\, V} }{ {\rm 4\, V} } \hspace{0.15cm}\underline{= 0.25}.$$

(3) Die Sprungantwort $σ(t)$ ist gleich dem Ausgangssignal $y(t)$, wenn am Eingang $x(t) = γ(t)$ anliegen würde.

Wegen $x_1(t) = 4 \hspace{0.05cm} \rm {V} · γ(t)$ gilt somit im Bereich von $0$ bis $T = 2 \ \rm ms$:

$$\sigma(t) = \frac{y_1(t)}{ {\rm 4\, V} } = 0.5 \cdot\big( {t}/{T} - 0.5 ({t}/{T})^2\big).$$

Zum Zeitpunkt $t = T = 2 \ \rm ms$ erreicht die Sprungantwort ihren Endwert $0.25$.
Für $t = T/2 = 1 \ \rm ms$ ergibt sich der Zahlenwert $3/16 \; \underline{\: = \: 0.1875}$.
Beachten Sie bitte, dass die Sprungantwort $σ(t)$ ebenso wie die Sprungfunktion $γ(t)$ keine Einheit besitzt.

rechts

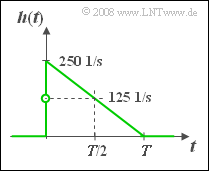
(4) Die Sprungantwort $σ(t)$ ist das Integral über die Impulsantwort $h(t)$.

Damit ergibt sich $h(t)$ aus $σ(t)$ durch Differentiation nach der Zeit.
Im Bereich $0 < t < T$ gilt deshalb:

$$h(t) = \frac{{\rm d}\hspace{0.1cm}\sigma(t)}{{\rm d}t}= 0.5 \cdot\left( \frac{1}{T} - 0.5 (\frac{2t}{T^2})\right) = \frac{0.5}{T} \cdot (1- \frac{t}{T})$$

$$\Rightarrow \hspace{0.2cm} h(t = {\rm 1\, ms}) = h(t = T/2) = \frac{0.25}{T} \hspace{0.15cm}\underline{= 125 \cdot{1}/{ {\rm s} } },$$

$$\Rightarrow \hspace{0.2cm} h(t = {\rm 2\, ms}) = h(t = T) \hspace{0.15cm}\underline{= 0}.$$

Für $t < 0$ und $t ≥ T$ gilt stets $h(t)=0$.
Der Wert $h(t = 0)$ bei exakt $t = 0$ muss aus dem Mittelwert zwischen links- und rechtsseitigem Grenzwert ermittelt werden:

$$h(t=0) = {1}/{2} \cdot \left[ \lim_{\varepsilon \hspace{0.03cm} \to \hspace{0.03cm}0} h(- \varepsilon)+ \lim_{\varepsilon \hspace{0.03cm} \to \hspace{0.03cm} 0} h(+ \varepsilon)\right] = \left[ 0 + {0.5}/{T}\right] = {0.25}/{T}= 250 \cdot{1}/{ {\rm s} }.$$

rechts

(5) Der Rechteckimpuls $x_2(t)$ kann auch als die Differenz zweier um $±T/2$ verschobener Sprünge dargestellt werden:

$$x_2(t) = A \cdot \big[\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big].$$

Damit ist das Ausgangssignal gleich der Differenz zweier um $±T/2$ verschobener Sprungantworten:

$$y_2(t) = A \cdot \big[\sigma(t + {T}/{2}) - \sigma(t - {T}/{2})\big].$$

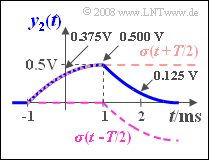
Für $t = \: -T/2 = -1\ \rm ms$ gilt $y_2(t) \;\underline{ = 0}$.

Für die weiteren betrachteten Zeitpunkte erhält man wie in der Grafik angegeben:

$$y_2(t = 0) = A \cdot \big[\sigma(0.5 \cdot T) - \sigma(-0.5 \cdot T)\big] = {\rm 2\, V}\cdot \left[0.1875 - 0\right] \hspace{0.15cm}\underline{= {\rm 0.375\, V}},$$

$$y_2(t = T/2) = y_2(t = 1\,{\rm ms}) =A \cdot \big[\sigma( T) - \sigma(0)\big] = {\rm 2\, V}\cdot \left[0.25 - 0\right] \hspace{0.15cm}\underline{= {\rm 0.5\, V}},$$

$$y_2(t = T) = A \cdot \big[\sigma(1.5 \cdot T) - \sigma(0.5 \cdot T)\big] = {\rm 2\, V}\cdot \big[0.25 - 0.1875\big] \hspace{0.15cm}\underline{= {\rm 0.125\, V}}.$$