Exercise 3.13: Code Rate and Reliability
Claude E. Shannon's channel coding theorem states, among other things, that a channel can be used to transmit with an arbitrarily small block error probability as long as the code rate $R$ is not greater than the channel capacity $C$. However, this result can only be achieved with channel coding for very large block lengths: $n → ∞$, which is associated with an arbitrarily large effort.
This statement is based on information-theoretical laws that Shannon himself established. However, Shannon does not say what this "infinitely good" channel coding must look like, he only proves that it exists.
The inverse of the channel coding theorem states that no error-free transmission is possible with a rate $R > C$. There is then no coding system with a vanishingly small error probability, no matter how elaborate and sophisticated the coding.
Rather, two bounds can be specified for the case $R > C$ :
- If one transmits via a "discrete memoryless channel" $\rm (DMC)$ with a rate $R$ greater than the channel capacity $C$, there is a lower bound for the bit error probability:
- $$ p_{\rm B} \ge H_{\rm bin}^{-1} \left (1 - {C}/{R} \right) > 0 \hspace{0.05cm}.$$
- If the bit error probability is not to exceed the value $p_{\rm B}$ after best possible decoding, the rate must not exceed a certain limit:
- $$ R \le \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.05cm}.$$
In this exercise, these equations are to be evaluated numerically using the binary entropy function
- $$ H_{\rm bin}( p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}.$$
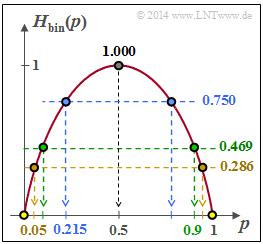
$H_{\rm bin}(p)$ is sketched above. Because of $0 < p_B ≤ 1$ and $0 < C/R < 1$ the argument of the function $H_{\rm bin}(⋅)$ and its inverse $H_{\rm bin}^{ –1 }(⋅)$ is always between $0$ and $1$.
Hints:
- The exercise belongs to the chapter Application to digital signal transmission.
- Reference is made in particular to the page Rate, channel capacity and bit error probability.
- The values of the binary entropy function are provided, for example, by the interactive applet Entropy and approximations of binary message sources .
- The values of the binary entropy function are provided, for example, by the interactive applet Entropy and approximations of binary message sources .
Questions
Solution
- $$ p_{\rm B,\hspace{0.05cm} min} = H_{\rm bin}^{-1} \left (1 - \frac{C}{R} \right) = H_{\rm bin}^{-1} (0.75) \hspace{0.05cm}.$$
From the graph on the data page (blue marking) we can read: $ p_{\rm B,\hspace{0.05cm} min} \hspace{0.15cm} \underline {=0.215} \hspace{0.05cm}.$
(2) By rearranging the above equation, we obtain with $H_{\rm bin}(p_{\rm B})$ from the graph:
- $$\begin{align*} R_{\rm max} = \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.10:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.469}\hspace{0.15cm} \underline {=0.942} \hspace{0.05cm},\\ \Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.05:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.286}\hspace{0.15cm} \underline {=0.700}\hspace{0.05cm}.\end{align*}$$
(3) Proposed solutions 2 and 3 are correct:
- For the binary entropy function, by definition:
- $$H_{\rm bin}( p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$
- Both terms are positive. From this follows the proposed solution 2: $H_{\rm bin}(p) = p · \log_2 \, (1/p)$.
- The difference is given by the second term of the binary entropy function:
- $$ H_{\rm bin}( p) - p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} = (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$
- This term becomes smaller the smaller $p$ is.
- Proposed solution 3 is therefore also correct, as the following calculations show:
- $$ p_{\rm B} = 10^{-3}\text{:} \hspace{0.3cm} 0.999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.999}= 1.4420 \cdot 10^{-3} \hspace{0.05cm},$$
- $$p_{\rm B} = 10^{-4}\text{:} \hspace{0.3cm} 0.9999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9999}= 1.4427 \cdot 10^{-4} \hspace{0.05cm},$$
- $$p_{\rm B} = 10^{-5}\text{:} \hspace{0.3cm} 0.99999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.99999}= 1.4427 \cdot 10^{-5} \hspace{0.05cm}.$$
(4) All proposed solutions are correct:
- The expression $R/C$ gives the upper bound according to the inverse channel coding theorem. For $p_{\rm B} = 10^{ –3 }$ , the following bound is obtained:
- $$R/C ≤ 1.01154 \hspace{0.5cm} ⇒ \hspace{0.5cm} R/C - 1 ≤ 1.154 · 10^{ –2 }.$$
- Proposition 2 takes into account the approximation according to subtask (3) . Since the denominator is now increased, $R′/C < R/C$, for example, applies for
- $$p_{\rm B} = 10^{ –3 }\text{:}\hspace{0.5cm} R′/C = 1.01007 · 10^{ –2 }.$$
- This is also an upper bound, somewhat safer than the first bound $R/C$.
- The bound $R′′ < R′$ is obtained by replacing $1/(1 – ε)$ by $1 + ε$ ersetzt $(ε$ is positive$)$. For example, for $p_{\rm B} = 10^{–3}$ one now obtains
- $$R′′/C = 1.00997 \hspace{0.5cm} ⇒ \hspace{0.5cm} R′′/C - 1 ≤ 0.997 · 10^{–2}.$$
- $R′′′$ according to the last suggestion is identical to $R′′$ and well suited for rollover calculations with integer exponent $i$ .
For the logarithm to the base ten, the numerical value $\lg(2) ≈ 0.30103 applies.$
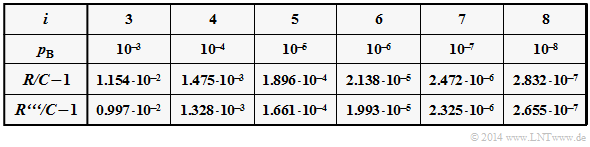
The table shows for different bit error probabilities $p_{\rm B}$ the deviations
- of the first bound $(R/C-1)$ and
- of the last approximation $(R'''/C-1)$.
One can see the good agreement of both specifications.