Exercise 4.5: Mutual Information from 2D-PDF

Given joint PDF

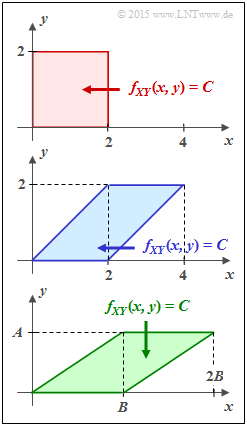
Given here are the three different two-dimensional regions $f_{XY}(x, y)$, which in the task are identified by their fill colors with

red joint PDF,
blue joint PDF,
green joint PDF,

respectively. Within each of the regions shown, let $f_{XY}(x, y) = C = \rm const.$

For example, the mutual information between the continuous random variables $X$ and $Y$ can be calculated as follows:

$$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$

For the differential entropies used here, the following equations apply:

$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[f_X(x)\big] \hspace{0.1cm}{\rm d}x \hspace{0.05cm},$$

$$h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.55cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm},$$

$$h(XY) = \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \big[ f_{XY}(x, y) \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$

For the two marginal probability density functions, the following holds:

$$f_X(x) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{Y}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}y\hspace{0.05cm},$$

$$f_Y(y) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}x\hspace{0.05cm}.$$

Hints:

The exercise belongs to the chapter Mutual information with continuous input.

Let the following differential entropies also be given:

If $X$ is triangularly distributed between $x_{\rm min}$ and $x_{\rm max}$, then:

$$h(X) = {\rm log} \hspace{0.1cm} [\hspace{0.05cm}\sqrt{ e} \cdot (x_{\rm max} - x_{\rm min})/2\hspace{0.05cm}]\hspace{0.05cm}.$$

If $Y$ is equally distributed between $y_{\rm min}$ and $y_{\rm max}$, then holds:

$$h(Y) = {\rm log} \hspace{0.1cm} \big [\hspace{0.05cm}y_{\rm max} - y_{\rm min}\hspace{0.05cm}\big ]\hspace{0.05cm}.$$

All results should be expressed in "bit". This is achieved with $\log$ ⇒ $\log_2$.

Questions

$I(X; Y) \ = \ $

$\ \rm bit$

$I(X; Y) \ = \ $

$\ \rm bit$

$I(X; Y) \ = \ $

$\ \rm bit$

	The two-dimensional PDF $f_{XY}(x, y)$ results in a parallelogram.
	One of the random variables $(X$ or $Y)$ is uniformly distributed.
	The other random variable $(Y$ or $X)$ is triangularly distributed.

Solution

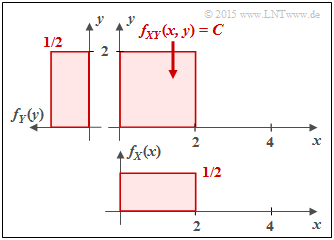
"Red" probability density functions;
! Note: Ordinate of $f_{Y}(y)$ is directed to the left !

(1) For the rectangular two-dimensional PDF $f_{XY}(x, y)$ there are no statistical dependences between $X$ and $Y$ ⇒ $\underline{I(X;Y) = 0}$.

Formally, this result can be proved with the following equation:

$$I(X;Y) = h(X) \hspace{-0.05cm}+\hspace{-0.05cm} h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(XY)\hspace{0.02cm}.$$

The red area of the two-dimensional PDF $f_{XY}(x, y)$ is $F = 4$.
Since $f_{XY}(x, y)$ is constant in this area and the volume under $f_{XY}(x, y)$ must be equal to $1$, the height is $C = 1/F = 1/4$.
From this follows for the differential joint entropy in "bit":

$$h(XY) \ = \ \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_{XY}(x, y) ] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$

$$\Rightarrow \hspace{0.3cm} h(XY) \ = \ \ {\rm log}_2 \hspace{0.1cm} (4) \cdot \hspace{0.02cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y = 2 \,{\rm bit}\hspace{0.05cm}.$$

It is considered that the double integral is equal to $1$ . The pseudo-unit "bit" corresponds to the "binary logarithm" ⇒ "log₂".

Furthermore:

The marginal probability density functions $f_{X}(x)$ and $f_{Y}(y)$ are rectangular ⇒ uniform distribution between $0$ and $2$:

$$h(X) = h(Y) = {\rm log}_2 \hspace{0.1cm} (2) = 1 \,{\rm bit}\hspace{0.05cm}.$$

"Blue" probability density functions

Substituting these results into the above equation, we obtain:

$$I(X;Y) = h(X) + h(Y) - h(XY) = 1 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit} = 0 \,{\rm (bit)} \hspace{0.05cm}.$$

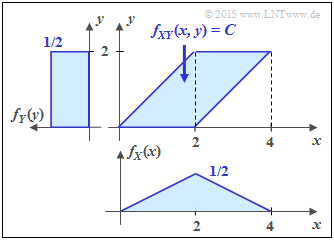
(2) Also for this parallelogram we get $F = 4, \ C = 1/4$ as well as $h(XY) = 2$ bit.

Here, as in subtask (1) , the variable $Y$ is uniformly distributed between $0$ and $2$ ⇒ $h(Y) = 1$ bit.

In contrast, $X$ is triangularly distributed between $0$ and $4$ $($with maximum at $2)$.
This results in the same differential entropy $h(Y)$ as for a symmetric triangular distribution in the range between $±2$ (see specification sheet):

$$h(X) = {\rm log}_2 \hspace{0.1cm} \big[\hspace{0.05cm}2 \cdot \sqrt{ e} \hspace{0.05cm}\big ] = 1.721 \,{\rm bit}$$

$$\Rightarrow \hspace{0.3cm} I(X;Y) = 1.721 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit}\hspace{0.05cm}\underline{ = 0.721 \,{\rm (bit)}} \hspace{0.05cm}.$$

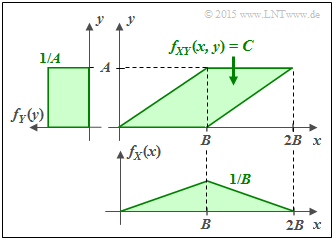
"„Green" probability density functions

(3) The following properties are obtained for the green conditions:

$$F = A \cdot B \hspace{0.3cm} \Rightarrow \hspace{0.3cm} C = \frac{1}{A \cdot B} \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} h(XY) = {\rm log}_2 \hspace{0.1cm} (A \cdot B) \hspace{0.05cm}.$$

The random variable $Y$ is now uniformly distributed between $0$ and $A$ and the random variable $X$ is triangularly distributed between $0$ and $2B$ $($with maximum at $B)$:

$$h(X) \ = \ {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ e}) \hspace{0.05cm},$$ $$ h(Y) \ = \ {\rm log}_2 \hspace{0.1cm} (A)\hspace{0.05cm}.$$

Thus, for the mutual information between $X$ and $Y$:

$$I(X;Y) \ = {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ {\rm e}}) + {\rm log}_2 \hspace{0.1cm} (A) - {\rm log}_2 \hspace{0.1cm} (A \cdot B)$$

$$\Rightarrow \hspace{0.3cm} I(X;Y) = \ {\rm log}_2 \hspace{0.1cm} \frac{B \cdot \sqrt{ {\rm e}} \cdot A}{A \cdot B} = {\rm log}_2 \hspace{0.1cm} (\sqrt{ {\rm e}})\hspace{0.15cm}\underline{= 0.721\,{\rm bit}} \hspace{0.05cm}.$$

Other examples of 2D PDF $f_{XY}(x, y)$

$I(X;Y)$ thus independent of th PDF parameters $A$ and $B$.

(4) All of the above conditions are required. However, the requirements (2) and (3) are not satisfied for every parallelogram.

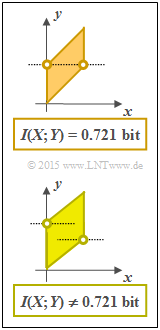
The adjacent graph shows two constellations, where the random variable $X$ is equally distributed between $0$ and $1$ in each case.
For the top graph, the plotted points lie at a height ⇒ $f_{Y}(y)$ is triangularly distributed ⇒ $I(X;Y) = 0.721$ bit.
The lower composite PDF has a different mutual information, since the two plotted points are not at the same height
⇒ the PDF $f_{Y}(y)$ here has a trapezoidal shape.
Feeling, I guess $I(X;Y) < 0.721$ bit, since the two-dimensional area is more approaching a rectangle. If you still feel like it, so check this statement.