Exercise 1.3: Fictional University Somewhere

Fictional University Somewhere

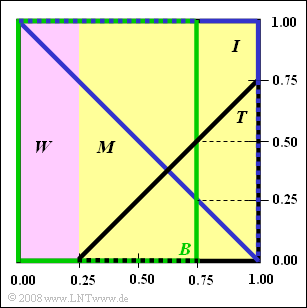
From the adjacent graph you can read some information about $\rm FUS$ (Fictional University Somewhere) ablesen. The whole square represents the universal set $G$ of $960$ students. Of these

$25\%$ female (set $W$, purple rectangle),
$75\%$ male (set $M$, yellow rectangle).

At the university there are the faculties of

Theologie (set $T$, black triangle),
Information Technology (set $I$, blue triangle),
Business Administration (set $B$, green triangle).

Each student must be assigned to at least one of these faculties, but can belong to two or three faculties at the same time.

(Bitte diesen Satz überprüfen) The areas in the above diagram are to scale, so you can easily indicate the (percentage) occupancy figures using the numerical values given and simple geometric considerations.

Hints:

The exercise belongs to the chapter Set Theory Basics.

The topic of this chapter is illustrated with examples in the (German language) learning video Mengentheoretische Begriffe und Gesetzmäßigkeiten $\Rightarrow$ Set Theoretical Concepts and Laws.

Fragebogen

$N_{\rm T} \ = \ $

	$I$ ist eine Teilmenge von $M$.
	$W$ ist eine Teilmenge von $B$.
	$W$ und $M$ ergeben zusammen ein vollständiges System.
	$B$, $I$ und $T$ ergeben zusammen ein vollständiges System.
	$W$ und $T$ sind disjunkte Mengen.
	Die Vereinigungsmenge von $B$, $I$ und $T$ ergibt die Grundmenge $G$.
	Die Schnittmenge von $B$, $I$ und $T$ ergibt die leere Menge $\phi$.

$\text{Pr}\big[\text{IT-Studentin}\big] \ = \ $

$\ \%$

$\text{Pr}\big[\text{ein Studienfach}\big] \ = \ $

$\ \%$

$\text{Pr}\big[\text{drei Studienfächer}\big] \ = \ $

$\ \%$

$\text{Pr}\big[\text{zwei Studienfächer}\big] \ = \ $

$\ \%$

Musterlösung

Solution

(1) Aus einfachen geometrischen Überlegungen kommt man zu den Ergebnissen:

$${\rm Pr}(B) = 3/4 \cdot 1 = 3/4\hspace{0.3cm}(\text{absolut:}\ 720),$$

$${\rm Pr}(I) = {1}/{2}\cdot 1\cdot 1 = 1/2\hspace{0.3cm}(\text{absolut:} \ 480),$$

$${\rm Pr}(T) = {1}/{2} \cdot {3}/{4} \cdot {3}/{4} = {9}/{32} \hspace{0.3cm}(\text{absolut:}\ 270)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}N_{\rm T} \;\underline{= 270}.$$

(2) Richtig sind die Lösungsvorschläge 2, 3, 5 und 6 ⇒ die Lösungsvorschläge 1, 4, 7 sind demzufolge falsch:

Es gibt auch IT-Studentinnen, wenn auch nur sehr wenige.
Die Vereinigung von $B$, $I$ und $T$ ergibt die Grundmenge, aber kein vollständiges System (nicht alle Kombinationen von $B$, $I$ und $T$ sind zueinander disjunkt).
Aus dem gleichen Grund ergibt auch die Schnittmenge von $B$, $I$ und $T$ nicht die leere Menge.

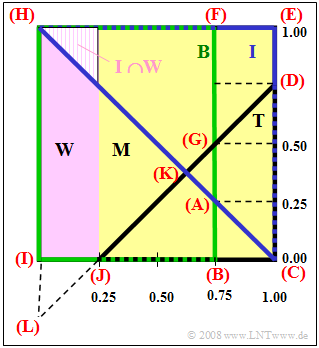
Geometrische Lösung eines Wahrscheinlichkeitsproblems

(3) Eine IT-Studentin ist mengentheoretisch die Schnittmenge aus $I$ und $W$
(in der Grafik links oben dargestellt als schraffierte Fläche):

$$\text{Pr[IT-Studentin] = Pr}(I \cap W) = {1}/{2}\cdot {1}/{4} \cdot {1}/{4} = {1}/{32} \hspace{0.15cm}\underline { \thickapprox 3.13 \%}.$$

In Worten: Unter den $960$ Studierenden gibt es $30$ IT–Studentinnen.

(4) Die Wahrscheinlichkeit ist als Summe dreier Einzelwahrscheinlichkeiten berechenbar:

$$ \text{Pr[ein Studienfach] = Pr}( \overline{B} \cap \overline{I} \cap T) + {\rm Pr}( \overline{B} \cap I \cap \overline{T}) + {\rm Pr}( \it B \cap \overline{I} \cap \overline{T}).$$

Jede einzelne Wahrscheinlichkeit entspricht einer Fläche im Venndiagramm und kann durch Addition bzw. Subraktion von Dreiecken oder Rechtecken bestimmt werden (siehe Grafik):

$$p_1 = {\rm Pr}( \overline{B} \cap \overline{I} \cap T) = {\rm Dreieck\ (ABC)}= \frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm}\frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm}\frac{1}{4}= \frac{1}{32}\hspace{0.1cm}\underline{\approx 0.0313},$$

$$p_2 ={\rm Pr}( \overline{B} \cap I \cap \overline{T}) = {\rm Viereck\hspace{0.1cm}(DEFG)}= \frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4}\hspace{0.02cm}+ \hspace{0.02cm}\frac{1}{2}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4} = \frac{3}{32}\hspace{0.1cm}\underline{\approx 0.0938},$$

$$p_3 = {\rm Pr}( B \cap \overline{I} \cap \overline{T}) ={\rm Viereck\hspace{0.1cm}(HIJK)}= {\rm Dreieck\hspace{0.1cm}(HLK)}- {\rm Dreieck\hspace{0.1cm}(ILJ)} = \frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{5}{4}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{5}{8}\hspace{0.02cm} - \hspace{0.02cm}\frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{1}{4} \cdot \frac{1}{4} = \frac{23}{64}\hspace{0.1cm}\underline{\approx 0.3594}.$$

$\text{Oder:}\hspace{0.3cm}$

$$p_3 = {\rm Dreieck\hspace{0.1cm}(HIC)}- {\rm Dreieck\hspace{0.1cm}(KJC)} ={1}/{2}\hspace{0.1cm} \cdot \hspace{0.1cm} 1 \hspace{0.1cm} \cdot \hspace{0.1cm} 1 \hspace{0.1cm} - \hspace{0.1cm}{1}/{2}\hspace{0.05cm} \cdot \hspace{0.1cm} {3}/{4} \cdot {3}/{8} = {23}/{64}.$$

Die Summe dieser drei Wahrscheinlichkeiten führt zum Endergebnis $ \text{Pr[ein Studienfach] } = 31/64 \;\underline {\approx 48.43 \%}$.

(5) Diese Wahrscheinlichkeit wird durch das $\text{Dreieck (AGK)}$ ausgedrückt. Dieses hat die Fläche

$$\rm Pr[drei\hspace{0.1cm}Studienf\ddot{a}cher] = {1}/{2}\cdot {1}/{4}\cdot {1}/{8} = {1}/{64}\hspace{0.15cm}\underline{\approx 1.56 \%}.$$

(6) Die drei Ereignisse

"nur ein Studienfach",
"zwei Studienfächer" und
"drei Studienfächer"

bilden ein vollständiges System. Damit erhält man mit den Ergebnissen der letzten Teilaufgaben:

$$\rm Pr[zwei\hspace{0.1cm}Studienf\ddot{a}cher] = 1- \text{Pr[ein Studienfach] } - \rm Pr[drei\hspace{0.1cm}Studienf\ddot{a}cher]= 1- {31}/{64} - {1}/{64} \hspace{0.15cm}\underline{= 50\%}.$$

Zum genau gleichen Ergebnis – aber mit deutlich mehr Aufwand – käme man auf dem direkten Weg entsprechend:

$${\rm Pr[zwei\hspace{0.1cm}Studienf\ddot{a}cher] = Pr}(B\cap I \cap\overline{T}) + {\rm Pr}(B\cap\overline{I}\cap{T}) + {\rm Pr}(\overline{B}\cap I \cap T).$$