Exercise 1.2: Decimal/Binary Converter

Logical circuit for D/B converting

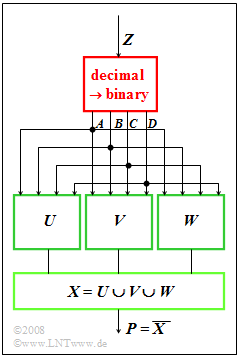
A number generator $Z$ supplies decimal values in the range $1$ to $15$.

These are converted into binary numbers (block outlined in red).
The output consists of the four binary values $A$, $B$, $C$ and $D$ with decreasing significance.
For example $Z = 11$ delivers the binary values

$$ A = 1, \ B = 0, \ C = 1, \ D = 1. $$

Set-theoretically, this can be represented as follows:

$$ Z = 11\qquad\widehat{=}\qquad A \cap\overline{ B} \cap C \cap D.$$

Three more Boolean expressions are formed from the binary quantities $A$, $B$, $C$ and $D$ and their union set is denoted $X$ :

\[ U = A \cap \overline{D} \]

\[ V = \overline{A} \cap B \cap \overline{D} \]

$$W,\; {\rm where} \; \, \overline{W} = \overline{A} \cup \overline{D} \cup (\overline{B} \cap C) \cup (B \cap \overline{C}). $$

Note that $Z = 0 \ ⇒ \ A = B = C = D = 0$ is already excluded by the number generator.
Note also that not all input quantities $A$, $B$, $C$ and $D$ are used to calculate all intermediate quantities $U$, $V$ and $W$, resp.

Hints:

The exercise belongs to the chapter Set theory basic.
The topic of this chapter is illustrated with examples can be found in the (German language) learning video:

"Mengentheoretische Begriffe und Gesetzmäßigkeiten" ⇒ "Set-theoretical terms and laws".

Questions

Solution

(1) The event $U$ contains

those numbers greater/equal to eight $(A = 1)$,
which are even $(D = 0)$: $8, 10, 12, 14$

⇒ Proposed solutions 2 and 4 are correct.

(2) The event $V$ consists of the two numbers $4$ (binary 0100) and $6$ (binary 0110) ⇒ The correct solutions are 1 and 3.

Auxiliary Venn diagram

(3) For the event $W$, de Morgan's theorem holds:

$$\overline W = \overline A \cup \overline D \cup (\overline B \cap C) \cup (B \cap \overline C) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W = \overline{\overline W} = A \cap D \cap (\overline{\overline B \cap C}) \cap (\overline{B \cap \overline C}).$$

Using de Morgan's theorems, it further follows:

$$ W = A \cap D \cap (B \cup \overline C) \cap (\overline B \cup C).$$

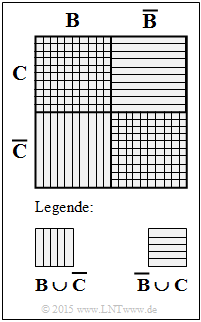
Finally, using the Boolean relation $(B \cup \overline C) \cap (\overline B \cup C) = (B \cap C) \cup (\overline B \cap \overline C)$ we obtain (see sketch):

$$W = (A \cap B \cap C \cap D) \cup (A \cap \overline B \cap \overline C \cap D).$$

Thus, $W$ contains the numbers $15$ and $9$ ⇒ only the proposed solution 1 is correct.

(4) The union of $U$, $V$ and $W$ contains the following numbers: $4, 6, 8, 9, 10, 12, 14, 15$.

Accordingly, the set $P$ as the complement of this union is:

$$P = {\{1, 2, 3, 5, 7, 11, 13\}}.$$

These are exactly the prime numbers which can be represented with four bits ⇒ Proposed solution 2.

	$U$ contains two elements.
	$U$ contains four elements.
	The smallest element of $U$ is $4$.
	The largest element of $U$ is $14$.

	$V$ contains two elements.
	$V$ contains four elements.
	The smallest element of $V$ is $4$.
	The largest element of $V$ is $14$.

	$W$ contains two elements.
	$W$ contains four elements.
	The smallest element of $W$ is $4$.
	The largest element of $W$ is $14$.

	$P$ contains all powers of two.
	$P$ contains all prime numbers.
	$P$ describes the empty set $\phi$.
	$P$ is identical with the universal set $G = {1,2, \ \text{...} \ , 15}$.