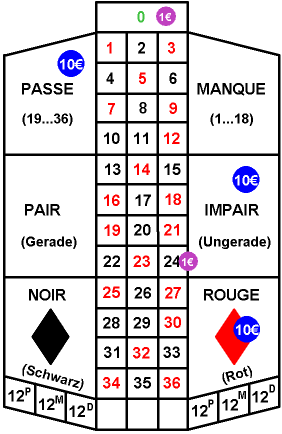
Exercise 1.3Z: Winning with Roulette?
In roulette, a winning number $Z$ is determined in each game by means of a ball and a roulette wheel, where we want to assume that all possible numbers $Z \in \{0, 1, 2, \ \text{...} \ , 36 \}$ are equally probable.
The players can now bet on a single number or on a group of numbers with chips of different value. Some of the possibilities and the corresponding winnings will be briefly explained here on the basis of the chips bet by a player (see graph):
- If a player bets on a number (in the example on "0"), he would get back $35$ times his stake as winnings in addition to his bet.
- If a player bets on a group of numbers with three fields (in the example, the 1-euro chip for the numbers from "22" to "24"), he would receive $ 11$ times his stake as winnings in addition to his bet.
- If a player bets on a group of numbers with $ 18$ fields (for example, the 10-euro chips on "Rouge", on "Impair" and on "Passe"), he will receive the same amount back as winnings in addition to his bet.
- If the number drawn does not belong to one of the squares he occupies, his bet is lost.
Hints:
- The exercise belongs to the chapter Set Theory Basics.
- Enter any losses as negative winnings in the following questions.
- The topic of this chapter is illustrated with examples in the (German language) learning video
- Mengentheoretische Begriffe und Gesetzmäßigkeiten $\Rightarrow$ "Set-Theoretical Concepts and Laws".
Questions
Solution
- He wins $33$ euro, if $0$ is drawn. It follows that:
- $$G_1 =\rm {36}/{37}\cdot (-1\hspace{0.1cm} euro) + {1}/{37}\cdot (33\hspace{0.1cm} euro) \hspace{0.15cm}\underline {= - 0.081\hspace{0.1cm} euro\hspace{0.1cm}(Loss)}.$$
(2) The player wins and loses nothing unless the zero is drawn. If the zero appears, he loses his bet:
- $$G_2 = \rm {1}/{37}\cdot (-2\hspace{0.1cm} euro)\hspace{0.15cm}\underline { = -0.054 \hspace{0.1cm}euro \hspace{0.1cm}(Loss)}.$$
(3) If "red" is drawn, he wins nine euro.
- If "zero" comes, he effectively wins $25$ euro.
- If "black" is drawn, he loses his entire bet of $11$ euro:
- $$G_3 = \rm {18}/{37}\cdot (10 -1) + {1}/{37}\cdot (35-10) + {18}/{37}\cdot (-10-1)\hspace{0.15cm}\underline { = - 0.297\hspace{0.1cm}euro}.$$
(4) He gets the highest winning at $Z_{\rm desire} \; \underline{ = 23} $. Then four of his five chips win:
- $$G_4 = \rm 10\hspace{0.1cm}(Red) + 10\hspace{0.1cm}(Passe) + 10\hspace{0.1cm}(Impair) + \rm 11\hspace{0.1cm}(between \hspace{0.1cm}22\hspace{0.1cm} and \hspace{0.1cm}24) - 1 \hspace{0.1cm}(not \hspace{0.1cm}0) \hspace{0.15cm}\underline {= 40 \hspace{0.1cm}euro}.$$
- If, on the other hand, the "zero" comes, he wins only $\rm 35 - 31 = 4 \ euro$.
(5) No, unfortunately not. On statistical average, the house always wins.