Exercise 2.2: Multi-Level Signals

• Return to book

Two similar multi-stepped signals

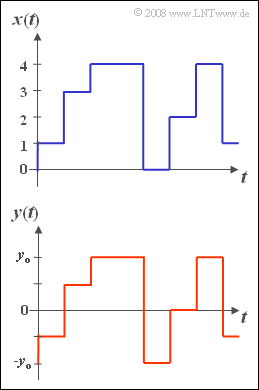
Let the rectangular signal  $x(t)$  be dimensionless and can only have the current values  $0, \ 1, \ 2, \ \text{...} \ , \ M-2, \ M-1$  with equal probability. The upper graph shows this signal for the special case  $M = 5$.

The rectangular zero mean signal  $y(t)$  can also assume  $M$  different values. 

• It is restricted to the range from  $-y_0 \le y \le +y_0$.
• In the graph below you can see the signal  $y(t)$, again for the level number  $M = 5$.

Hints:

• The exercise belongs to the chapter  Moments of a Discrete Random Variable.
• Fur numerical calculations,  use  $y_0 = \rm 2\hspace{0.05cm}V$.
• The topic of this chapter is illustrated with examples in the  (German language)  learning video
      "Momentenberechnung bei diskreten Zufallsgrößen"   ⇒   "Calculating Moments for Discrete-Valued Random Variables"

Questions

1

What is the linear mean  $m_x$  of the random variable  $x$  for  $M= 5$?

$m_x \ = \ $

2

What is the variance  $\sigma_x^2$  of the random variable  $x$  in general and for  $M= 5$?

$\sigma_x^2\ = \ $

3

Calculate the mean  $m_y$  of the random variable  $y$  for  $M= 5$.

$m_y \ = \ $ $\ \rm V$

4

What is the variance  $\sigma_y^2$  of the random variable  $y$  in general and for  $M= 5$?  Consider the result from  (2).

$\sigma_y^2\ = \ $ $\ \rm V^2$

Solution

Solution

(1)  One obtains by averaging over all possible signal values for the linear mean:

$$m_{\it x}=\rm \sum_{\mu=0}^{\it M-{\rm 1}} \it p_\mu\cdot x_{\mu}=\frac{\rm 1}{\it M} \cdot \sum_{\mu=\rm 0}^{\it M-\rm 1}\mu=\frac{\rm 1}{\it M}\cdot\frac{(\it M-\rm 1)\cdot \it M}{\rm 2}=\frac{\it M-\rm 1}{\rm 2}.$$

• In the special case  $M= 5$  the linear mean results in  $m_x \;\underline{= 2}$.

(2)  Analogously to  (1)  one obtains for the root mean square:

$$m_{\rm 2\it x}= \rm \sum_{\mu=0}^{\it M -\rm 1}\it p_\mu\cdot x_{\mu}^{\rm 2}=\frac{\rm 1}{\it M}\cdot \sum_{\mu=\rm 0}^{\rm M- 1}\mu^{\rm 2} = \frac{\rm 1}{\it M}\cdot\frac{(\it M-\rm 1)\cdot \it M\cdot(\rm 2\it M-\rm 1)}{\rm 6} = \frac{(\it M-\rm 1)\cdot(\rm 2\it M-\rm 1)}{\rm 6}.$$

• In the special case $M= 5$  the root mean square results in  $m_{2x} {=6}$.
• From this, the variance can be calculated using Steiner's theorem:

$$\sigma_x^{\rm 2}=m_{\rm 2\it x}-m_x^{\rm 2}=\frac{(\it M-\rm 1)\cdot(\rm 2\it M-\rm 1)}{\rm 6}-\frac{(\it M-\rm 1)^{\rm 2}}{\rm 4}=\frac{\it M^{\rm 2}-\rm 1}{\rm 12}.$$

• In the special case  $M= 5$  the result for the variance  $\sigma_x^2 \;\underline{= 2}$.

(3)  Because of the symmetry of  $y$,  it holds independently of  $M$:

$$m_y \;\underline{= 0}.$$

(4)  The following relation holds between  $x(t)$  and  $y(t)$:

$$y(t)=\frac{2\cdot y_{\rm 0}}{M-\rm 1}\cdot \big[x(t)-m_x\big].$$

• From this it follows for the variances:

$$\sigma_y^{\rm 2}=\frac{4\cdot y_{\rm 0}^{\rm 2}}{( M - 1)^{\rm 2}}\cdot \sigma_x^{\rm 2}=\frac{y_{\rm 0}^{\rm 2}\cdot (M^{\rm 2}- 1)}{3\cdot (M- 1)^{\rm 2}}=\frac{y_{\rm 0}^{\rm 2}\cdot ( M+ 1)}{ 3\cdot ( M- 1)}.$$

• In the special case  $M= 5$  this results in:

$$\it \sigma_y^{\rm 2}= \frac {\it y_{\rm 0}^{\rm 2} \cdot {\rm 6}}{\rm 3 \cdot 4}\hspace{0.15cm} \underline{=\rm2\,V^{2}}.$$