Exercise 4.3: Pointer Diagram Representation
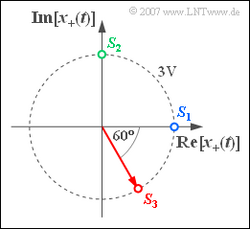
Wir betrachten ein analytisches Signal x+(t), welches durch das gezeichnete Diagramm in der komplexen Ebene festgelegt ist. Je nach Wahl der Signalparameter ergeben sich daraus drei physikalische BP–Signale x1(t), x2(t) und x3(t), die sich durch verschiedene Startpunkte Si = xi(t = 0) unterscheiden (blauer, grüner und roter Punkt). Zudem seien auch die Winkelgeschwindigkeiten der drei Konstellationen unterschiedlich:
- Das analytische Signal x1+(t) beginnt bei S1 = 3 V. Die Winkelgeschwindigkeit ist ω1 = π · 104 1/s.
- Das Signal x2+(t) beginnt beim grünen Startpunkt S2 = j · 3 V und dreht gegenüber x1+(t) mit doppelter Winkelgeschwindigkeit (ω2 = 2 · ω1).
- Das Signal x3+(t) beginnt beim rot markierten Ausgangspunkt S3 = 3 V · exp(–jπ/3) und dreht mit gleicher Geschwindigkeit wie das Signal x2+(t).
Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 4.2.
Fragebogen
Musterlösung
$$x_1(t) = 3\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi \cdot {\rm 5 \hspace{0.05cm} kHz}\cdot t) .$$
c) Wegen ω2 = 2ω1 beträgt nun die Frequenz f2 = 2 · f1 = 10 kHz. Die Phase ergibt sich mit dem Startzeitpunkt S2 zu exp(–j · φ2) = j, das heißt φ2 = –π/2 (–90°). Somit lautet die Zeitfunktion:
$$x_2(t) = 3\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot t + 90^\circ) = -3\hspace{0.05cm}{\rm V} \cdot {\sin} ( 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot t ).$$
Dieses Signal ist somit „minus–sinusförmig”, was auch direkt am Zeigerdiagramm abgelesen werden kann. Der Realteil von x2+(t) zum Zeitpunkt t = 0 ist 0. Da der Zeiger entgegen dem Uhrzeigersinn dreht, ergibt sich zunächst ein negativer Realteil. Nach einer viertel Umdrehung ist x2(T/4) = –3V. Dreht man nochmals in Schritten von 90° entgegen dem Uhrzeigersinn weiter, so ergeben sich die Signalwerte 0V, 3V und 0V. d) Diese Teilaufgabe kann analog zu den Fragen b) und c) gelöst werden: f3 = 10 kHz, φ3 = 60°. e) Der Zeiger benötigt für eine Umdrehung genau die Periodendauer T3 = 1/f3 = 0.1 ms (= t1). f) Das analytische Signal startet bei S3 = 3V · e– j60°. Dreht das Signal um 120° weiter, so ergibt sich genau der gleiche Realteil. Es gilt dann mit t2 = t1/3 = 0.033 ms folgende Beziehung:
$$x_3(t = t_2) = x_3(t = 0) = 3\hspace{0.05cm}{\rm V} \cdot {\cos} ( 60^\circ) = 1.5\hspace{0.05cm}{\rm V} .$$