Exercise 2.10: SSB-AM with Channel Distortions
Let us consider the transmission of the source signal
- $$q(t) = 2\,{\rm V} \cdot \cos(2 \pi f_2 t) + 2\,{\rm V} \cdot \cos(2 \pi f_4 t)$$
over a Gaussian bandpass channel with center frequency $f_{\rm M} = 48 \ \rm kHz$. This is different from the carrier frequency $f_{\rm T} = 50 \ \rm kHz$ used in modulation. The frequencies $f_2$ and $f_4$ stand fro $f = 2 \ \rm kHz$ und $f = 4 \ \rm kHz$, respectively.
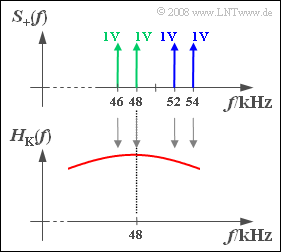
We will now investigate the following modulation methods with respect to the spectrum $S_+(f)$ of the analytical signal as shown in the upper graph:
- DSB–AM $($all four spectral lines at $46 \ \rm kHz$, $48 \ \rm kHz$, $52 \ \rm kHz$ and $54 \ \rm kHz)$,
- USB–AM $($only blue spectral lines at $52 \ \rm kHz$ and $54 \ \rm kHz)$,
- LSB–AM $($only green spectral lines at $46 \ \rm kHz$ and $48 \ \rm kHz)$.
In each case, a synchronous demodulator is used to first convert the receiver-side carrier signal
- $$ z_{\rm E} (t) = \left\{ \begin{array}{c} 2 \cdot z(t) \\ 4 \cdot z(t) \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{with}} \\ \end{array}\begin{array}{*{20}c} {\rm ZSB} \hspace{0.05cm}, \\ {\rm USB, LSB} \hspace{0.05cm} \\ \end{array}$$
by multiplication and then completely suppresses the components by twice the carrier frequency. Thus, with an ideal channel $H_{\rm K}(f) = 1$ , $v(t) = q(t)$ would hold in all cases.
The Gaussian channel considered here is given by the following auxiliary values:
- $$ H_{\rm K}(f = 46\ {\rm kHz}) = 0.968,\hspace{0.3cm}H_{\rm K}(f = 48\ {\rm kHz}) = 1.000,\hspace{0.3cm} H_{\rm K}(f = 52\ {\rm kHz}) = 0.882,\hspace{0.3cm}H_{\rm K}(f = 54\ {\rm kHz}) = 0.754\hspace{0.05cm}.$$
In each case, write the sink signal in the form.
- $$v(t) = A_2 \cdot \cos(2 \pi f_2 \cdot (t - \tau_2)) + A_4 \cdot \cos(2 \pi f_4 \cdot (t - \tau_4))\hspace{0.05cm}.$$
All calculations are to be carried out for both a perfect phase synchronization $(Δϕ_{\rm T} = 0)$ as well as for a phase offset of $Δϕ_{\rm T} = 30^\circ$ . This is present, for example, if the transmit-side carrier signal is cosine-shaped and the receiver-side carrier is:
- $$ z_{\rm E} (t) = A_{\rm E} \cdot \cos(\omega_{\rm T} \cdot t - 30^\circ) . $$
Hints:
- This exercise belongs to the chapter Single-Sideband Modulation.
- Reference will also be made to the chapter nbsp; Synchronous Demodulation.
Questions
Musterlösung
- $$\alpha_2 = {1}/{2} \cdot \left[ H_{\rm K}(f = 48\,{\rm kHz}) + H_{\rm K}(f = 52\,{\rm kHz})\right] = 0.981,$$
- $$\alpha_4 = {1}{2} \cdot \left[ H_{\rm K}(f = 46\,{\rm kHz}) + H_{\rm K}(f = 54\,{\rm kHz})\right] = 0.861\hspace{0.05cm}.$$
- Damit ergeben sich die Amplituden $A_2\hspace{0.15cm}\underline{ = 1.882 \ \rm V}$ und $A_4\hspace{0.15cm}\underline{ = 1.722 \ \rm V}$.
(2) Bei ZSB führt ein Phasenversatz zwischen den Trägerfrequenzen von Sender und Empfänger nur zu einer für alle Frequenzen gleichen Dämpfung:
- $$A_2 = \cos (30^\circ) \cdot 1.882\,{\rm V} \hspace{0.15cm}\underline {= 1.630\,{\rm V}},$$
- $$A_4 = \cos (30^\circ) \cdot 1.722\,{\rm V} = 1.491\,{\rm V}\hspace{0.05cm}.$$
- Die Laufzeiten sind $τ_2\hspace{0.15cm}\underline {= 0}$ und $τ_4 = 0$.
(3) Bei OSB–AM wird der Dämpfungsfaktor $α_2$ allein von $H_{\rm K}(f = 52\ \rm kHz)$ bestimmt.
- Da der prinzipielle Amplitudenverlust der OSB um den Faktor $2$ durch eine größere Trägeramplitude ausgeglichen wird, gilt:
- $$A_2 = 0.882 \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.764\,{\rm V}},$$
- $$A_4 = 0.754 \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.508\,{\rm V}} \hspace{0.05cm}.$$
(4) Analog zur Lösung der Teilaufgabe (3) erhält man hier:
- $$ A_2 = H_{\rm K}(f = 48\,{\rm kHz}) \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 2\,{\rm V}},$$
- $$A_4 = H_{\rm K}(f = 46\,{\rm kHz}) \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.936\,{\rm V}} \hspace{0.05cm}.$$
(5) Bei der USB–AM lautet das Empfangssignal:
- $$r(t) = 1\,{\rm V} \cdot \cos( \omega_{\rm 48} \cdot t) + 0.968\,{\rm V} \cdot \cos( \omega_{\rm 46} \cdot t)\hspace{0.05cm}.$$
- Durch Multiplikation mit dem empfangsseitigen Trägersignal $z_{\rm E}(t) = 4 \cdot \cos( \omega_{\rm 50} \cdot t - \Delta \phi_{\rm T})$ erhält man nach Anwendung des trigonometrischen Additionstheorems:
- $$v(t) = r(t) \cdot z_{\rm E}(t) = \hspace{0.15cm}\underline { 2.000\,{\rm V}} \cdot \cos( \omega_{\rm 2} \cdot t - \Delta \phi_{\rm T})+\hspace{0.15cm}\underline { 1.936\,{\rm V}} \cdot \cos( \omega_{\rm 4} \cdot t - \Delta \phi_{\rm T}) + {\rm Anteile \hspace{0.15cm}um \hspace{0.15cm}} 2f_{\rm T}\hspace{0.05cm}$$
- $$ \Rightarrow \hspace{0.3cm} A_2 \hspace{0.15cm}\underline {= 2\,{\rm V}},\hspace{0.5cm} A_4 \hspace{0.15cm}\underline {= 1.936\,{\rm V}}.$$
- Unter Berücksichtigung des nachfolgenden Tiefpassfilters kann hierfür auch geschrieben werden:
- $$ v(t) = A_2 \cdot \cos( \omega_{\rm 2} \cdot (t - \tau_2))+ A_4 \cdot \cos( \omega_{\rm 4} \cdot (t - \tau_4))\hspace{0.05cm}.$$
- Die Amplituden sind gegenüber Teilaufgabe (4) unverändert. Für die Laufzeiten erhält man mit $Δϕ_{\rm T} = π/6$:
- $$ \tau_2 = \frac {\Delta \phi_{\rm T}}{2 \pi \cdot f_2} = \frac {\pi /6}{2 \pi \cdot 2\,{\rm kHz}} \hspace{0.15cm}\underline {\approx 41.6\,{\rm µ s}},\hspace{0.5cm} \tau_4 = \frac {\Delta \phi_{\rm T}}{2 \pi \cdot f_4}= \frac {\tau_2}{2}\hspace{0.15cm}\underline {\approx 20.8\,{\rm µ s}} \hspace{0.05cm}.$$
(6) Richtig sind der erste und der letzte Lösungsvorschlag:
- Auch bei ESB führen Dämpfungsverzerrungen auf dem Kanal ausschließlich zu Dämpfungsverzerrungen bezüglich $v(t)$.
- Phasenverzerrungen gibt es nur bei einem Demodulator mit Phasenversatz bei eine Einseitenbandmodulation.
- Bei der ZSB–AM hätte ein solcher Phasenversatz keine Verzerrungen zur Folge, sondern nur eine frequenzunabhängige Dämpfung.
- Zu Phasenverzerrungen bezüglich $v(t)$ kommt es bei ZSB–AM und ESB–AM auch, wenn solche bereits auf dem Kanal auftreten.