Exercise 3.11: Chebyshev's Inequality

Exemplary Chebyshevsch barrier

If nothing else is known about a random size $x$ than only

the mean value $m_x$ and
the rms $\sigma_x$,

so the Chebyshev's Inequality an upper bound on the probability that $x$ deviates by more than one value from its mean value $\varepsilon$ is given.

This bound is:

$${\rm Pr}(|x-m_x|\ge \varepsilon) \le {\sigma_x^{\rm 2}}/{\varepsilon^{\rm 2}}.$$

To explain:

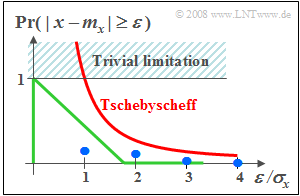
In the graph, this upper bound is drawn in red.
The larger curve shows the actual probability in the uniform distribution.
The blue points are for the exponential distribution.

From this plot it can be seen that the Chebyshev's Inequality is only a very rough bound.
It should be used only if really only the mean and the rms are known from the random size.

Values of the complementary Gaussian error function

Hints:

The exercise belongs to the chapter Further Distributions.
In particular, reference is made to the page Chebyshev's inequality .

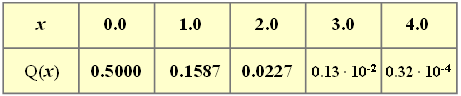
On the right, values of the complementary Gaussian error function ${\rm Q}(x)$ are given.

Questions

	Conceivably, a random variable with ${\rm Pr}(\|x -m_x> \| \ge 3\sigma_x) = 1/4$.
	"Chebyshev" yields für $\varepsilon < \sigma_x$ no information.
	${\rm Pr}(\|x -m_x> \| \ge \sigma_x)$ is identically zero for large $\varepsilon$ if $x$ is bounded.

${\rm Pr}(|x -m_x | \ge 3 \sigma_x) \ = \ $

$\ \%$

${\rm Pr}(|x -m_x | \ge 3 \sigma_x) \ = \ $

$\ \%$

Solution

(1) Correct are the proposed solutions 2 and 3:

The first statement is false. Chebyshev's inequality provides the bound here $1/9$.
For no distribution can the probability considered here be equal $1/4$ .
For $\varepsilon < \sigma_x$ Chebyshev yields a probability greater $1$. This information is useless.
The last statement is true. For example, in the uniform distribution:

$${\rm Pr}(| x- m_x | \ge \varepsilon)=\left\{ \begin{array}{*{4}{c}} 1-{\varepsilon}/{\varepsilon_{\rm 0}} & \rm f\ddot{u}r\hspace{0.1cm}{\it \varepsilon<\varepsilon_{\rm 0}=\sqrt{\rm 3}\cdot\sigma_x},\rm 0 & \rm else. \end{array} \right. $$

(2) For the Gaussian distribution holds:

$$p_k={\rm Pr}(| x-m_x| \ge k\cdot\sigma_{x})=\rm 2\cdot \rm Q(\it k).$$

This results in the following numerical values (in brackets: bound according to Chebyshev):

$$k= 1\text{:}\hspace{0.5cm} {\rm Pr}(|x-m_x| \ge \sigma_{x}) = 31.7 \% \hspace{0.3cm}(100 \%),$$

$$k= 2\text{:}\hspace{0.5cm} {\rm Pr}(|x-m_x| \ge 2 \cdot \sigma_{x}) = 4.54 \% \hspace{0.3cm}(25 \%),$$

$$k= 3\text{:}\hspace{0.5cm} {\rm Pr}(|x-m_x| \ge 3 \cdot\sigma_{x})\hspace{0.15cm}\underline{ = 0.26 \%} \hspace{0.3cm}(11.1 \%),$$

$$k= 4\text{:}\hspace{0.5cm} {\rm Pr}(|x-m_x| \ge 4 \cdot \sigma_{x}) = 0.0064 \% \hspace{0.3cm}(6.25 \%).$$

(3) Without restricting generality, we set $\lambda = 1$ ⇒ $m_x = \sigma_x = 1$. Then holds:

$${\rm Pr}(|x - m_x| \ge k\cdot\sigma_{x}) = {\rm Pr}(| x-1| \ge k).$$

Since in this special case the random variable is always $x >0$ , it further holds:

$$p_k= {\rm Pr}( x \ge k+1)=\int_{k+\rm 1}^{\infty}\hspace{-0.15cm} {\rm e}^{-x}\, {\rm d} x={\rm e}^{-( k + 1)}.$$

This yields the following numerical values for the exponential distribution:

$$k= 1\text{:}\hspace{0.5cm} {\rm Pr}(|x-m_x| \ge \sigma_{x}) \rm e^{-2}= \rm 13.53\%,$$

$$k= 2\text{:}\hspace{0.5cm} {\rm Pr}(|x-m_x| \ge 2 \cdot \sigma_{x})= \rm \rm e^{-3}=\rm 4.97\% ,$$

$$k= 3\text\text{:}\hspace{0.5cm} {\rm Pr}(|x-m_x| \ge 3 \cdot\sigma_{x})= \rm \rm e^{-4}\hspace{0.15cm}\underline{ =\rm 1.83\% },$$

$$k= 4\text{:}\hspace{0.5cm} {\rm Pr}(|x-m_x| \ge 4 \cdot \sigma_{x}) = \rm e^{-5}= \rm 0.67\%.$$