Exercise 3.10Z: Rayleigh? Or Rice?

• Return to book

Does the present PDF describe Rayleigh or Rice?

The probability density function of the random variable  $x$  is given as follows:

$$f_x(x)=\frac{\it x}{\lambda^{2}}\cdot{\rm e}^{-x^{\rm 2}/(\lambda^{\rm 2})}.$$

Correspondingly, for the associated distribution function:

$$F_x(r)= {\rm Pr}(x \le r) = 1-{\rm e}^{- r^{\rm 2}/(2 \lambda^{\rm 2})}.$$

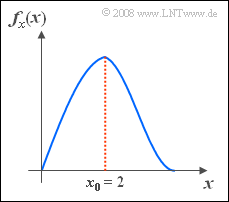
• It is known that the value  $x_0 = 2$  occurs most frequently.
• This also means that the PDF  $f_x(x)$  is maximum at  $x = x_0 $ .

Hints: This exercise belongs to the chapter  Further Distributions.

• In particular, reference is made to the pages  Rayleigh PDF  and  Rice PDF .

• You can check your results with interactive applet  PDF, CDF and moments of special distributions .
• Consider the following definite integral in the solution:

$$\int_{0}^{\infty}x^{\rm 2}\cdot {\rm e}^{ -x^{\rm 2}/\rm 2} \, {\rm d}x=\sqrt{{\pi}/{\rm 2}}.$$

Questions

1

Which of the following statements are true?

	It is a rice-distributed random size.
	It is a rayleigh distributed random size.
	The 3rd order central moment   ⇒   $\mu_3$  is zero.
	The kurtosis has the value  $K_x = 3$.

2

What is the numerical value of the distribution parameter  $\lambda$ here?

$\lambda \ = \ $

3

What is the probability that  $x$  is less than  $x_0 = 2$ ?

${\rm Pr}(x < x_0 ) \ = \ $ $\ \%$

4

What is the mean value of the random size $x$? Interpretation.

$m_x \ = \ $

5

With what probability is  $x$  larger than its mean  $m_x$?

${\rm Pr}(x > m_x) \ = \ $ $\ \%$

Solution

Solution

(1)  Correct is only the second proposed solution.

• Because of the given PDF there is no Rice distribution, but a Rayleigh distribution.
• This is asymmetric around the mean  $m_x$  so that  $\mu_3 \ne 0$ .
• Only in the case of a smoothly distributed random size does the kurtosis  $K = 3$.
• For the Rayleigh distribution, a larger value  $(K = 3.245)$ is obtained due to more pronounced PDF–emitters, independent of  $\lambda$.

(2)  The derivative of the PDF with respect to  $x$  yields:

$$\frac{{\rm d} f_x(x)}{{\rm d} x} = \frac{\rm 1}{\lambda^{\rm 2}}\cdot{\rm e}^{ -{x^{\rm 2}}/({2 \lambda^{\rm 2}})}+\frac{ x}{ \lambda^{\rm 2}}\cdot{\rm e}^{ -{x^{\rm 2}}/({ 2 \lambda^{\rm 2}})}\cdot(-\frac{2 x}{2 \lambda^{\rm 2}}).$$

• From this follows as the equation of determination for  $x_0$  (only the positive solution is meaningful):

$$\frac{1}{\lambda^{\rm 2}}\cdot{\rm e}^{ -{x_{\rm 0}^{\rm 2}}/{(2 \lambda^{\rm 2}})}\cdot(\rm 1-{\it x_{\rm 0}^{\rm 2}}/{\it \lambda^{\rm 2}})=0 \quad \Rightarrow \quad {\it x}_0=\it \lambda.$$

• Thus, we obtain for the distribution parameter  $\lambda = x_0\hspace{0.15cm}\underline{= 2}$.

(3)  The probability we are looking for is equal to the distribution function at the point  $r = x_0 = \lambda$:

$${\rm Pr}(x<x_{\rm 0})={\rm Pr}( x \le x_{\rm 0})= F_x(x_{\rm 0})=1-{\rm e}^{-{\lambda^{\rm 2}}/({ 2 \lambda^{\rm 2}})}=1-{\rm e}^{-0.5}\hspace{0.15cm}\underline{=\rm 39.3\%}.$$

(4)  For example, the mean can be calculated using the following equation:

$$m_x=\int_{-\infty}^{+\infty}\hspace{-0.45cm}x\cdot f_x(x)\,{\rm d}x=\int_{\rm 0}^{\infty}\frac{\it x^{\rm 2}}{\it \lambda^{\rm 2}} \cdot \rm e^{-{\it x^{\rm 2}}/({\rm 2\it \lambda^{\rm 2}})}\,{\rm d}\it x = \sqrt{{\rm \pi}/{\rm 2}}\cdot \it \lambda\hspace{0.15cm}\underline{=\rm 2.506}.$$

• The mean  $m_x$  is of course larger than  $x_0$  $(=$ maximum value of the PDF$)$, since the PDF is bounded downward but not upward.

(5)  In general, for the sought probability:

$${\rm Pr}(x>m_x)=1- F_x(m_x).$$

• With the given distribution function and the result of the subtask  (4)  we obtain:

$${\rm Pr}(x>m_x)={\rm e}^{-{m_x^{\rm 2}}/({ 2\lambda^{\rm 2})}}={\rm e}^{-\pi/ 4}\hspace{0.15cm}\underline{\approx \rm 45.6\%}.$$