Exercise 3.5Z: Antenna Areas

Two antenna areas: $K$ and $G$

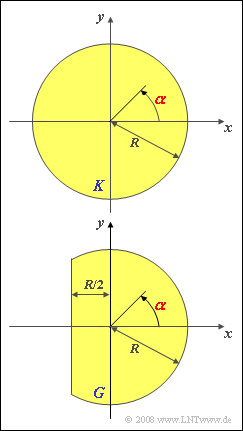
We first consider – as sketched in the image above – a receiving antenna serving a circular area $K$. It is assumed that this antenna can detect all signals incident at different angles $\alpha$ equally well:

According to the sketch, the angle $\alpha$ refers to the $x$–axis.
The value $\alpha = 0$ therefore means that the signal is moving towards the antenna in the direction of the negative $x$–axis.

Further we assume:

The range of values of the angle of incidence $\alpha$ with this definition $-\pi < \alpha \le +\pi$.
There are very many users in the coverage area whose positions $(x, y)$ are "statistically distributed" over the area $K$.

From subtask (5) we assume the coverage area $G$ outlined below.

Because of an obstacle, the $x$–coordinate of all participants must now be greaterö&space;than $-R/2$.
Also in the coverage area $G$ the subscribers would again be "statistically distributed".

Hint:

The exercise belongs to the chapter Uniformly Distributed Random Variables.

Questions

$f_\alpha(\alpha = 0) \ = \ $

	The expected value is ${\rm E}[\alpha] = 0$.
	The expected value is ${\rm E}[\alpha] \ne 0$.

$\sigma_\alpha \ = \ $

${\rm Pr}(-π/4 ≤ α ≤ +π/4) \ = \ $

$\ \%$

$\alpha_0 \ = \ $

$ \ \rm rad$

$\alpha_0 \ = \ $

$ \ \rm degrees$

	The PDF has the same course "outside" as "inside".
	The PDF is "outside" identically zero.
	The PDF decreases towards the edges in this area.
	The PDF increases towards the edges in this area.

${\rm Pr}(-π/4 ≤ α ≤ +π/4) \ = \ $

$\ \%$

$f_\alpha(\alpha = 0) \ = \ $

Solution

(1) There is a uniform distribution and it is true for the PDF in the range $-\pi < \alpha \le +\pi$:

$$f_\alpha(\alpha)={\rm 1}/({\rm 2\cdot \pi}).$$

For $\alpha = 0$ this gives – as for all allowed values also – the PDF value :$$f_\alpha(\alpha =0) \hspace{0.15cm}\underline{=0.159}.$$

(2) It holds ${\rm E}\big[\alpha\big] = 0$ ⇒ Answer 1.

It has no effect that $\alpha = +\pi$ is allowed, but $\alpha = -\pi$ is excluded.

(3) For the variance of the angle of incidence $\alpha$ holds:

$$\sigma_{\alpha}^{\rm 2}=\int_{-\rm\pi}^{\rm\pi}\hspace{-0.1cm}\it\alpha^{\rm 2}\cdot \it f_{\alpha}(\alpha)\,\,{\rm d} \alpha=\frac{\rm 1}{\rm 2\cdot\it \pi}\cdot \frac{\alpha^{\rm 3}}{\rm 3}\Bigg|_{\rm -\pi}^{\rm\pi}=\frac{\rm 2\cdot\pi^{3}}{\rm 2\cdot\rm \pi\cdot \rm 3}=\frac{\rm \pi^2}{\rm 3} = \rm 3. 29. \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\sigma_{\alpha}\hspace{0.15cm}\underline{=1.814}.$$

(4) Since the given section of the circle is exactly one quarter of the total circle area, the probability we are looking for is

$${\rm Pr}(-π/4 ≤ α ≤ +π/4)\hspace{0.15cm}\underline{=25\%}.$$

The area $G$

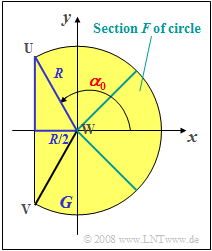
(5) From simple geometrical ¨considerations (right-angled triangle, marked dark blue in the adjacent sketch) one obtains the equation of determination for the angle $\alpha_0$:

$$\cos(\pi-\alpha_{\rm 0}) = \frac{R/ 2}{R}={\rm 1}/{\rm 2}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}\rm\pi-\it\alpha_{\rm 0}=\frac{\rm\pi}{\rm 3} \hspace{0.2cm}\rm( 60^{\circ}).$$

It follows $\alpha_0 = \pi/3\hspace{0.15cm}\underline{=2.094}.$
This corresponds $\alpha_0 \hspace{0.15cm}\underline{=120^\circ}$.

(6) Correct is the suggested solution 3:

The PDF $f_\alpha(\alpha)$ is f for a given angle $\alpha$ directly proportional to the distance $A$ between the antenna and the boundary line.
For $\alpha = \pm 2\pi/3 = \pm 120^\circ$ against $A = R$, for $\alpha \pm \pi = \pm 180^\circ$ against $A = R/2$.
In between the distance becomes successively smaller. This means: The PDF decreases towards the boundary.
The decrease follows the following course:

$$\it A=\frac{\it R/\rm 2}{\rm cos(\rm \pi-\it\alpha)}.$$

(7) The area $G$ can be calculated from the sum of the $240^\circ$–sector and the triangle formed by the vertices $\rm UVW$ :

$$G=\frac{\rm 2}{\rm 3}\cdot \it R^{\rm 2}\cdot{\rm \pi} \ {\rm +} \ \frac{\it R}{\rm 2}\cdot \it R\cdot \rm sin(\rm 60^{\circ}) = \it R^{\rm 2}\cdot \rm\pi\cdot (\frac{\rm 2}{\rm 3}+\frac{\rm \sqrt{3}}{\rm 4\cdot\pi}).$$

The probability we are looking for is given by the ratio of the areas $F$ and $G$ (see sketch):

$$\rm Pr(\rm -\pi/4\le\it\alpha\le+\rm\pi/4)=\frac{\it F}{\it G}=\frac{1/4}{2/3+{\rm sin(60^{\circ})}/({\rm 2\pi})}=\frac{\rm 0.25}{\rm 0.805}\hspace{0.15cm}\underline{=\rm 31.1\%}.$$

Although nothing has changed from point (4) at the area $F$ the probability now becomes larger by a factor $1/0.805 ≈ 1.242$ due to the smaller area $G$ .

(8) Since the overall PDF area is constantly equal $1$ and the PDF decreases at the boundaries, it must have a larger value in the range $|\alpha| < 2\pi/3$ than in (1).

With the results from (1) and (7) holds:

$$f_{\alpha}(\alpha = 0)=\frac{1/(2\pi)}{2/3+{\rm sin(\rm 60^{\circ})}/({\rm 2\pi})} = \frac{\rm 1}{{\rm 4\cdot\pi}/{\rm 3}+\rm sin(60^{\circ})}\hspace{0.15cm}\underline{\approx \rm 0.198}.$$

Like the probability in (7) also simultaneously the PDF value in the range $|\alpha| < 2\pi/3$ increases by a factor $1.242$ as the coverage area becomes smaller.