For spectral adaptation (shaping) of a digital signal to the characteristics of the channel, one uses so-called pseudo-ternary codes. In these codes, the binary source symbol sequence $\langle q_\nu \rangle$ is converted to a sequence $\langle c_\nu \rangle$ of ternary symbols according to a fixed rule:
- $$q_{\nu} \in \{ -1,\hspace{0.1cm} +1 \} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} c_{\nu} \in \{ -1, \hspace{0.1cm}0, \hspace{0.1cm}+1 \} .$$
The best known representative of this code class is the AMI code (from Alternate Mark Inversion). Here.
- the binary value $q_\nu = -1$ is always mapped to $c_\nu = 0$ ,
- while $q_\nu = +1$ is alternately represented by the ternary values $c_\nu = +1$ and $c_\nu = -1$ .
By convention, the ternary symbol $c_\nu = +1$ shall be selected at the first occurrence of $q_\nu = +1$ .
It is further assumed that
- the two possible source symbols are each equally probable and
- the source symbol sequence $\langle q_\nu \rangle $ has no internal statistical bindings.
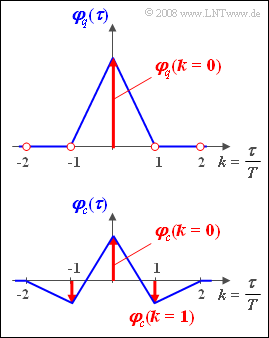
Thus, all discrete ACF values are zero except $\varphi_q(k=0)$:
- $$\varphi_q ( k \cdot T) = 0 \hspace{0.5cm} {\rm f alls} \hspace{0.5cm} k \not= 0.$$
Here $T$ denotes the distance between sources– or code symbols. Use the value $T = 1 \hspace{0.05cm} \rm µ s$.
The figure shows the given auto-correlation functions. Please note:
- In red are respectively the discrete-time representations ${\rm A} \{ \varphi_q(\tau) \}$ and ${\rm A} \{ \varphi_c(\tau) \}$ of the auto-correlation functions, each with the reference value $T$.
- The functions shown in blue indicate the continuous-time progressions $\varphi_q(\tau)$ and $\varphi_c(\tau)$ of the ACF, assuming square-wave pulses.
Hints:
- This exercise belongs to the chapter Power-Spectral Density.
- Reference is also made to the chapter Auto-Correlation Function as well as to the page Numerical PSD determination.
- Benutzen Sie die folgende Fourierkorrespondenz, wobei ${\rm \Delta} (t)$ einen um $t = 0$ symmetrischen Dreieckimpuls mit ${\rm \Delta} (t= 0) = 1$ und ${\rm \Delta} (t) = 0$ für $|t| \ge T$ bezeichnet:
- $${\rm \Delta} (t) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} T \cdot {\rm si}^2 ( \pi f T).$$
Questions
Solution
- Since $q_\nu$ can only take the values $-1$ and $+1$ , $\varphi_q(k=0)\hspace{0.15cm}\underline{= 1}$.
(2) Correct are the proposed solutions 1 and 3:
- The discrete-time ACF and its Fourier transform are:
- $${\rm A} \{ \varphi_q ( \tau ) \} = \varphi_q ( k = 0) \cdot T \cdot \delta (\tau) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{\it \Phi_q}( f) \} = \varphi_q ( k = 0) \cdot T = T.$$
- It is considered that $\varphi_q(k=0)= \sigma_q^2= 1$ This means:
- The periodic continuation of ${\rm P} \{ {\it \Phi}_q(f) \}$ thus gives the same value for all frequencies.
- In contrast, the continuous-time ACF can be represented as follows:
- $$ \varphi_q ( \tau ) = {\rm A} \{ \varphi_q ( \tau ) \} \star ( {\rm \delta} ( \tau) / T ).$$
- The associated Power spectral density spectrum (Fourier transform of the ACF) is then the product of the Fourier transforms of the two convolution terms:
- $$ {\it \Phi_q} ( f) = {\rm P} \{ {\it \Phi_q}( f) \} \cdot {\rm si}^2 (\pi f T ) = T \cdot {\rm si}^2 (\pi f T ) .$$
- Based on the chosen ACF interpolation (with straight line intercepts) from their samples, a $\rm si^2$-shaped PSD is obtained.
- A rectangular spectrum according to the proposed solution (2) would only occur with $\rm si$-shaped interpolation.
(3) The coded sequence is: $\langle +1, \ 0, -1, +1, \ 0, -1, +1, \ 0, \ 0, \ 0 \rangle$. Thus the 6th symbol is $c_6\hspace{0.15cm}\underline{= -1}$.
(4) The probabilities of occurrence of the values $-1$ , $\ 0$ and $+1$ are $0.25, 0.5, 0.25$. It follows:
- $$\varphi_c ( k = 0) = 0.25 \cdot (-1)^2 + 0.5 \cdot 0^2 +0.25 \cdot (+1)^2\hspace{0.15cm}\underline{ = 0.5}. $$
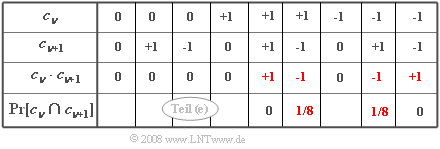
(5) For the ACF value at $k = 1$ consider the product $c_{\nu} \cdot c_{\nu+1}$. The combinations shown on the right are obtained.
- Only products $c_{\nu} \cdot c_{\nu+1} \ne 0$ with ${\rm Pr}\big[c_{\nu} \cdot c_{\nu+1}\big] \ne 0$:
- $$\varphi_c ( k = 1) = {\rm Pr} \big [( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \big ] \cdot (+1) \cdot (-1) + {\rm Pr} \big [ ( c_{\nu} = -1) \cap ( c_{\nu + 1} = +1) \big ] \cdot (-1) \cdot (+1).$$
- In the table, these terms are marked in red. Further:
- $$ {\rm Pr} \big [ ( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \big ] = $$
- $$ = {\rm Pr} ( c_{\nu} = +1) \cdot {\rm Pr} \left ( c_{\nu + 1} = -1 | c_{\nu } = +1) \right ) = \frac{1}{4} \cdot \frac{1}{2}= \frac{1}{8} . $$
- Here it is assumed that $+1$ occurs with probability $0.25$ and is followed by $-1$ only in half of the cases.
- The same result is obtained for the second contribution. Thus applies:
$$varphi_c ( k = 1) = \frac {1}{8} \cdot (+1)\cdot (-1) + \frac {1}{8} \cdot (-1)\cdot (+1) \hspace{0.15cm}\underline{= -0.25}.$$
- $$\varphi_c ( k = -1) = \varphi_c ( k = 1) \hspace{0.15cm}\underline{= -0.25}.$$
- To calculate $\varphi_c ( k = 2)$ it is necessary to average over $3^3 = 27$ combinations. The result is zero.
(6) The Fourier transform of the discrete-time ACF ${\rm A} \{ \varphi_c(\tau) \}$ is:
- $$P \{{\it \Phi_c}( f) \} = T\cdot \varphi_c ( k = 0) +2T \cdot \varphi_c ( k = 1) \cdot {\rm cos} ( 2 \pi f T ).$$
- With the result of the last subtask, it follows:
- $$P \{{\it \Phi}_c( f) \} = \frac {T}{2} (1 - {\rm cos} ( 2 \pi f T ) )= T \cdot {\rm sin}^2 ( \pi f T ).$$
- As shown in item (2), then, for the PSD – that is, the Fourier transform of $\varphi_c(\tau)$:
- $${\it \Phi_c}( f) = T \cdot {\rm sin}^2 ( \pi f T ) \cdot {\rm si}^2 ( \pi f T ) = T \cdot \frac {{\rm sin}^4 ( \pi f T )}{( \pi f T )^2 } .$$
- $$\Rightarrow \hspace{0.3cm} {\it \Phi_c}( f = 0) \hspace{0.15cm}\underline{= 0}, \hspace{0.8cm} {\it \Phi_c}( f = {\rm500 \hspace{0.1cm}kHz}) = T \cdot \frac {{\rm sin}^4 ( \pi /2 )}{( \pi /2 )^2 } = \frac {4 T}{\pi^2} \rm \hspace{0.15cm}\underline{= 0.405 \cdot 10^{-6} \ {1}/{Hz}}.$$