Exercise 3.10Z: Amplitude and Angle Modulation in Comparison

• Return to book

Characteristic curves illustrating the noise behavior for  $\rm AM$  and  $\rm WM$

Consider the transmission of a cosine signal with amplitude modulation   $\rm (AM)$  and angle modulation $\rm (WM)$. The following boundary conditions apply::

• Message frequency  $f_{\rm N} = 10 \ \rm kHz$,
• Transmission power  $P_{\rm S} = 100 \ \rm kW$,
• Channel transmission factor  $20 · \lg α_{\rm K} = -120 \ \rm dB$,
• noise power density  $N_0 = 10^{–16} \ \rm W/Hz$.

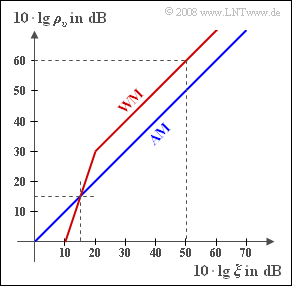
These system parameters are conveniently combined to form the performance parameter: $$ \xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$ The graph shows the resulting sink-to-noise ratio  $10 · \lg ρ_v$  as a function of the logarithmized performance parameter   $ξ$.

Hints:

• This exercise belongs to the chapter  Modulation Methods/Influence of Noise on Systems with Angle Modulation.
• Reference is also made to the page   Sink SNR and the performance parameter  and the chapter  Frequency Modulation.

• The following relationships hold:

$$\rho_{v } = \left\{ \begin{array}{c} \xi \\ {\eta^2}/2 \cdot\xi \\ 3{\eta^2}/2 \cdot\xi \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}l} {\rm DSB/SSB-AM \hspace{0.15cm}without \hspace{0.15cm}carrier} \hspace{0.05cm}, \\ {\rm PM \hspace{0.15cm}with \hspace{0.15cm}modulation\hspace{0.15cm}depth \hspace{0.15cm} \eta } \hspace{0.05cm}, \\ {\rm FM \hspace{0.15cm}with \hspace{0.15cm}modulation\hspace{0.15cm}depth \hspace{0.15cm} \eta }\hspace{0.05cm}. \\ \end{array}$$

• The bandwidths  $B_{\rm K}$  for angle modulation shall be selected according to the "Carson rule" to guarantee a distortion factor of  $K < 1\%$ :

$$ B_{\rm K} = 2 \cdot f_{\rm N} \cdot (\eta +2) \hspace{0.05cm}.$$

Questions

1

Calculate the logarithmized power parameter  $ξ$.

$10 · \lg \ ξ \ = \ $ $\ \rm dB$

2

What is the sink-to-noise ratio for the AM system?

$10 · \lg ρ_v \ = \ $ $\ \rm dB$

3

What special kind of AM might be present here?

	It could be a DSB-AM.
	It could be a SSB-AM.
	It could be an AM without a carrier.
	It could be an AM with an added carrier.

4

In the case of the DSB-AM, what is the required channel bandwidth  $B_{\rm K}$?

$B_{\rm K} \ = \ $ $\ \rm kHz$

5

What is the sink-to-noise ratio for the WM system?

$10 · \lg ρ_v \ = \ $ $\ \rm dB$

6

What is the minimum bandwidth required for the given PM system if  $K < 1\%$  is to apply?

$B_{\rm K} \ = \ $ $\ \rm kHz$

7

For $K < 1\%$ , die erforderliche Bandbreite, what is the required bandwidth if the WM system implements frequency modulation??

$B_{\rm K} \ = \ $ $\ \rm kHz$

8

All other parameters being equal, what is the minimum transmit power  $P_{\rm S}$  required for the WM system to be no worse than the AM system?

$P_{\rm S,\hspace{0.05cm}min} \ = \ $ $\ \rm W$

Solution

Solution

(1)  From  $20 · \lg α_{\rm K} = -120 \ \rm dB$  we get  $α_{\rm K} = 10^{–6}$.  Thus, with   $B_{\rm NF} = f_{\rm N}$, one obtains:

$$ \xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}= \frac{10^{-12} \cdot 10^{5}\;{\rm W}}{10^{-16}\;{\rm W/Hz} \cdot 10^{4}\;{\rm Hz}}= 10^5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\xi \hspace{0.15cm}\underline {= 50\,{\rm dB}}\hspace{0.05cm}.$$

(2)  From the graph, it can be seen that   $ρ_v = ξ$  holds for the AM system. Thus, the sinking signal-to-noise ratio is:

$$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }\hspace{0.15cm}\underline {= 50\,{\rm dB}}\hspace{0.05cm}.$$

(3)  The first three answers are correct:

• It is a DSB-AM or a SSB-AM without a carrier.
• DSB–AM and SSB–AM with a carrier can be ruled out.  In these instances, it would always be the case that   $ρ_v < \xi$ .

(4)  For DSB–AM,  $B_{\rm K} ≥ 2 · f_{\rm N}\hspace{0.15cm}\underline { = 20 \ \rm kHz}$  must hold.

(5) From the given graph, it can be seen that from about  $20 \ \rm dB$  onwards:

$$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }= 10 \cdot {\rm lg} \hspace{0.15cm}\xi + 10\,{\rm dB}. \hspace{0.3cm}{\rm Mit}\hspace{0.15cm}10 \cdot {\rm lg} \hspace{0.15cm}\xi = 50\,{\rm dB}\hspace{0.05cm}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }\hspace{0.15cm}\underline {= 60\,{\rm dB}}.$$

(6)  In the case of phase modulation:

$$ \rho_{v }= \frac{\eta^2}{2} \cdot \xi \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta^2 = \frac{2 \cdot \rho_{v }}{\xi} = 20\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta \approx 4.47 \hspace{0.05cm}.$$

• Thus, the channel bandwidth needed for 𝐾<1% must be:

$$B_{\rm K} \ge 2 \cdot f_{\rm N} \cdot (\eta +2) = 20\,{\rm kHz}\cdot 6.47 \hspace{0.15cm}\underline { \approx 130\,{\rm kHz}}\hspace{0.05cm}.$$

(7) Here, a smaller modulation index is sufficient, and thus a smaller bandwidth:

$${3}/{2}\cdot \eta^2 = 10\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta \approx 2.58 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}B_{\rm K} = 20\,{\rm kHz}\cdot 4.58 \hspace{0.15cm}\underline {\approx 91.6\,{\rm kHz}}\hspace{0.05cm}.$$

(8)  In the graph, one can see the so-called FM threshold effect.

• For  $10 · \lg \hspace{0.08cm} ξ = 15 \ \rm dB$  one obtains exactly the same sink SNR for the WM system as for the AM system.
• Thus, the transmit power can be   $35 \ \rm dB$  less than s  $100 \ \rm kW$:

$$ 10 \cdot {\rm lg} \hspace{0.15cm}\frac{P_{\rm S,\hspace{0.05cm}min}}{100\,{\rm kW}}= -35\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{P_{\rm S,\hspace{0.05cm}min}}{100\,{\rm kW}}\approx 0.0003\hspace{0.3cm}\Rightarrow \hspace{0.3cm}P_{\rm S,\hspace{0.05cm}min} \hspace{0.15cm}\underline {\approx 30\,{\rm W}}\hspace{0.05cm}.$$