Exercise 1.6: Root Nyquist System
From LNTwww
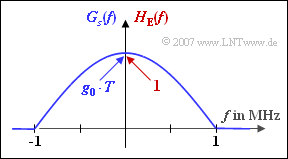
The diagram on the right shows
- the spectrum $G_{s}(f)$ of the basic transmission pulse,
- the frequency response $H_{\rm E}(f)$ of the receiver filter
of a binary and bipolar transmission system, which are identical in shape to each other:
- $$G_s(f) = \left\{ \begin{array}{c} A \cdot \cos \left( \frac {\pi \cdot f}{2 \cdot f_2} \right) \\ \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}}\\ \\ \\ \end{array} \begin{array}{*{20}c}|f| \le f_2 \hspace{0.05cm}, \\ \\ {\rm else }\hspace{0.05cm}, \\ \end{array}$$
- $$H_{\rm E }(f) = \left\{ \begin{array}{c} 1 \cdot \cos \left( \frac {\pi \cdot f}{2 \cdot f_2} \right) \\ \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}}\\ \\ \\ \end{array} \begin{array}{*{20}c}|f| \le f_2 \hspace{0.05cm}, \\ \\ {\rm else }\hspace{0.05cm}. \\ \end{array}$$
In the whole exercise $A = 10^{–6} \ \rm V/Hz$ and $f_{2} = 1 \ \rm MHz$ are valid.
- Assuming that the bit rate $R = 1/T$ is chosen correctly, the basic transmitter pulse $g_{d}(t) = g_{s}(t) ∗ h_{\rm E}(t)$ satisfies the first Nyquist criterion.
- For the associated spectral function $G_{d}(f)$, the rolloff thereby occurs cosinusoidally similar to a cosine rolloff spectrum.
- The rolloff factor $r$ is to be determined in this exercise.
Notes:
- The exercise belongs to the chapter Optimization of Baseband Transmission Systems.
- Numerical values of the Q-function are provided, for example, by the interactive applet Complementary Gaussian Error Functions.
- The crest factor is the quotient of the maximum value and the rms value of the transmitted signal and thus a measure of the intersymbol interfering at the transmitting end:
- $$C_{\rm S} = \frac{s_0}{\sqrt{E_{\rm B}/T}} = \frac{{\rm Max}[s(t)]}{\sqrt{{\rm E}[s^2(t)]}}= {s_0}/{s_{\rm eff}}.$$
Questions
Solution
(1) With the functions $G_{s}(f)$ and $H_{\rm E}(f)$, the spectrum of the basic transmitter pulse for $|f| \leq f_{2}$:
- $$G_d(f) = G_s(f) \cdot H_{\rm E}(f) = A \cdot \cos^2 \left( \frac {\pi \cdot f}{2 \cdot f_2} \right).$$
- According to the general definition of the cosine rolloff spectrum, the corner frequencies $f_{1} = 0$ and $f_{2} = 1\ \rm MHz$ are obtained.
- From this follows for the Nyquist frequency (symmetry point with respect to the rolloff):
- $$f_{\rm Nyq} = \frac{f_1 +f_2 } {2 } \hspace{0.1cm}\underline { = 0.5\,{\rm MHz}}\hspace{0.05cm}.$$
- The rolloff factor is
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 } \hspace{0.1cm}\underline {= 1} \hspace{0.05cm}.$$
- This means: $G_{d}(f)$ describes a $\cos^{2}$ spectrum.
(2) The relationship between Nyquist frequency and symbol duration $T$ is $f_{\rm Nyq} = 1/(2T)$.
- From this it follows for the bit rate $R = 1/T = 2 \cdot f_{\rm Nyq}\ \underline{= 1 \ \rm Mbit/s}$.
- Note the different units for frequency and bit rate.
(3) The first and third solutions are correct:
- This is an optimal binary system under the constraint of power limitation.
- The crest factor is not important under power limitation. With the conditions given here, $C_{\rm S} > 1$ would apply.
(4) The bit error probability of an optimal system can be calculated as follows:
- $$p_{\rm B} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right)\hspace{0.05cm}.$$
- In the given example, we obtain for the average energy per bit:
- $$E_{\rm B} = \ \int_{-\infty}^{+\infty}|G_s(f)|^2 \,{\rm d} f = A^2 \cdot \int_{-1/T}^{+1/T} H_{\rm Nyq}(f) \,{\rm d} f = \ \frac {A^2}{T} = \frac {(10^{-6}\,{\rm V/Hz})^2}{10^{-6}\,{\rm s}} = 10^{-6}\,{\rm V^2s}\hspace{0.05cm}.$$
- With $N_{0} = 8 \cdot 10^{–8} \ \rm V^{2}/Hz$, this further gives:
- $$p_{\rm B} = {\rm Q} \left( \sqrt{\frac{2 \cdot 10^{-6}\,{\rm V^2s}}{8 \cdot 10^{-8}\,{\rm V^2/Hz}}}\right)= {\rm Q} \left( \sqrt{25}\right)= {\rm Q} (5) \hspace{0.1cm}\underline {= 0.287 \cdot 10^{-6}}\hspace{0.05cm}.$$