Exercise 4.10: Binary and Quaternary
From LNTwww
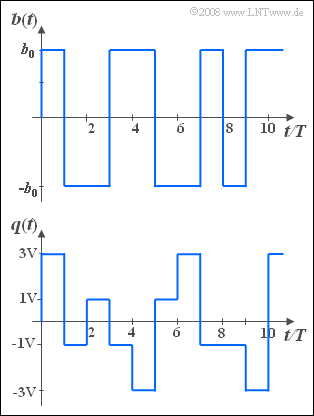
We consider here a binay signal $b(t)$ and a quaternary signal $q(t)$.
- The two signals are rectangular in shape. The duration of each rectangle is $T$ (symbol duration).
- The symbols represented by the pulse heights of the individual rectangular pulses $($with step number $M = 2$ or $M = 4)$ are statistically independent.
- Because of the bipolar signal constellation, both signals have no DC component if the symbol probabilities are chosen appropriately (symmetrically).
- Because of the latter property, it follows for the probabilities of the binary symbols:
- $${\rm Pr}\big[b(t) = +b_0\big] = {\rm Pr}\big[b(t) = -b_0\big] ={1}/{2}.$$
- In contrast, for the quarternary signal:
- $${\rm Pr}\big[q(t) = +3 \hspace{0.05cm}{\rm V}\big] = {\rm Pr}\big[q(t) = -3 \hspace{0.05cm}{\rm V}\big]= {1}/{6},$$
- $${\rm Pr}\big[q(t) = +1 \hspace{0.05cm}{\rm V}\big] = {\rm Pr}\big[q(t) = -1 \hspace{0.05cm}{\rm V}\big]= {2}/{6}.$$
Hint: This exercise belongs to the chapter Auto-Correlation Function.
Questions
Solution
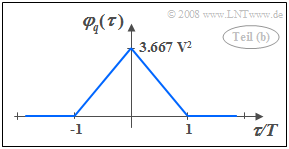
(1) The ACF value at the point $\tau = 0$ corresponds to the mean signal power, i.e. the variance of $q(t)$. For this holds:
- $$\varphi_q(\tau = 0)= {1}/{6 } \cdot ({\rm 3\,V})^2 + {2}/{6 } \cdot ({\rm 1\,V})^2 + {2}/{6 } \cdot (-{\rm 1\,V})^2 + {1}/{6 } \cdot (-{\rm 3\,V})^2= \rm {22}/{6 }\, \rm V^2\hspace{0.15cm}\underline{= \rm 3.667 \,V^2}.$$
(2) The individual symbols were assumed to be statistically independent.
- Therefore, and because of the lack of a DC component, for any integer value of $\nu$, the following applies here:
- $${\rm E} \big [ q(t) \cdot q ( t + \nu T) \big ] = {\rm E} \big [ q(t) \big ] \cdot {\rm E} \big [ q ( t + \nu T) \big ]\hspace{0.15cm}\underline{ = 0}.$$
- Thus, the ACF we are looking for has the shape sketched on the right.
- In the range $-T \le \tau \le +T$ the ACF is sectionwise linear, i.e. triangular, due to the rectangular pulse shape.
(3) The ACF $\varphi_b(\tau)$ of the binary signal is also identically zero due to the statistically independent symbols in the range $| \tau| > T$.
- For $-T \le \tau \le +T$ itnalso results in a triangular shape.
- For the second moment, one obtains:
- $$\varphi_b (\tau = 0) = b_{\rm 0}^{\rm 2}.$$
- With $b_0\hspace{0.15cm}\underline{= 1.915\, \rm V}$ the two auto-correlation functions $\varphi_q(\tau)$ and $\varphi_b(\tau)$ are identical.
(4) Correct are the proposed solutions 1, 3, and 4.
From the autocorrelation function we can actually determine:
- The period $T_0$: this is the same for the pattern signals and the ACF;
- the linear mean: root of the final value of the ACF for $\tau \to \infty$;
- the variance: difference of the ACF values of $\tau = 0$ and $\tau \to \infty$.
Cannot be determined:
- The probability density function $\rm (PDF)$:
despite $\varphi_q(\tau) =\varphi_b(\tau)$ ⇒ $f_q(q) \ne f_b(b)$; - the moments of higher order:
for their calculation one needs the PDF; - all phase relations and symmetry properties are not recognizable from the ACF.