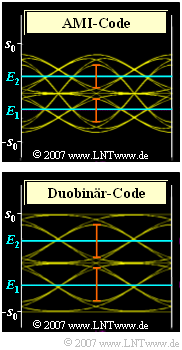
Exercise 3.5: Eye Opening with Pseudoternary Coding
From LNTwww
Eye diagrams with AMI and duobinary code
Three message transmission systems are considered, each with the following matching properties:
- NRZ rectangular pulses with amplitude $s_0 = 2 \, {\rm V}$,
- Coaxial cable with characteristic cable attenuation $a_* = 40 \, {\rm dB}$,
- AWGN noise with noise power density $N_0$,
- Receiver filter $H_{\rm E}(f) = 1/H_{\rm K}(f) \cdot H_{\rm G}(f) $ consisting of an ideal channel equalizer $H_{\rm K}(f)^{-1}$ and a Gaussian low-pass filter $H_{\rm G}(f)$ with normalized cutoff frequency $f_{\rm G} \cdot T \approx 0.5$.
- Threshold decision with optimal decision thresholds and optimal detection time $T_{\rm D} = 0$.
The system variants to be investigated in the exercise differ only in terms of the transmission code:
$\text{System A}$ uses a binary bipolar redundancy-free transmission signal. The following descriptive variables are known:
- Basic pulse values $g_0 = 1.56 \, {\rm V}$, $g_1 = g_{\rm –1} = 0.22 \, {\rm V}$, $g_2 = g_{\rm –2} = \, \text{ ...} \, \approx 0$
- $$\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{ 2} = g_{0} -g_{1}-g_{-1} = 1.12\,{\rm V} \hspace{0.05cm}.$$
- Noise rms value $\sigma_d \approx 0.2 \, {\rm V}$
- $$\Rightarrow \hspace{0.3cm}\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2\big]^2}{ \sigma_d^2}\approx 31.36\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \approx 15\,{\rm dB}\hspace{0.05cm}.$$
$\text{System B}$ uses AMI coding:
- Here the outer symbols $"+1"$ or $"–1"$ occur only in isolation.
- In the case of three consecutive symbols, the sequences "$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, +1, \, +1, \,\text{ ...}$" and "$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, 0, \, +1, \, \text{ ...} $" among others, are not possible,
- in contrast to the sequence "$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, –1, \, +1, \, \text{ ...} $".
$\text{System C}$ uses the duobinary code:
- Here the alternating sequence "$\hspace{-0.1cm} \text{ ...} \, , \, –1, \, +1, \, –1, \, \text{ ...} $" is excluded by the code, which has a favorable effect on the eye opening.
Notes:
- The exercise belongs to the chapter "Intersymbol Interference for Multi-Level Transmission".
- Not all of the numerical values given here are necessary to solve this exercise.
Questions
Solution
(1) Since the symbol rate is not changed in the AMI code compared to the redundancy-free binary system, the basic pulse values remain unchanged:
- $$g_0 = 1.56 \, {\rm V}, \ g_1 = g_{\rm –1} = 0.22 \, {\rm V}, \ g_2 = g_{\rm –2} \approx 0.$$
In pseudo-ternary coding, there are always two eye openings:
- The upper boundary line of the upper eye results in the AMI code as in the redundancy-free binary system:
- $$d_{\rm top}= g_0 - 2 \cdot g_1 \hspace{0.2cm}{\rm (associated} \hspace{0.1cm}{\rm sequence:}-1, +1, -1{\rm )} \hspace{0.05cm}.$$
- In contrast, for the lower boundary line of the upper eye:
- $$d_{\rm bottom}= g_1 \hspace{0.2cm}{\rm (associated} \hspace{0.1cm}{\rm sequence:}\hspace{0.2cm}0, \hspace{0.05cm}0, +1\hspace{0.2cm}{\rm bzw.}\hspace{0.2cm}+1, \hspace{0.05cm}0, \hspace{0.05cm}0{\rm )}\hspace{0.05cm}.$$
Thus, for the half eye opening, the following holds true:
- $${\ddot{o}(T_{\rm D})}/{2}= {1}/{2} \cdot (d_{\rm top} - d_{\rm bottom}) = {1}/{2} \cdot g_0 - {3}/{2} \cdot g_1 \hspace{0.15cm}\underline {= 0.45\,{\rm V}}\hspace{0.05cm}.$$
The corresponding equation for the redundancy-free binary system is:
- $${\ddot{o}(T_{\rm D})}/{2}= g_0 - 2 \cdot g_1 \hspace{0.05cm}.$$
(2) In terms of noise, there is no difference between the three systems since the same symbol rate is always present. It follows for the AMI code:
- $$\rho_{\rm U} = \frac{(0.45\,{\rm V})^2}{(0.2\,{\rm V})^2} = 5.06 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 7\,{\rm dB}} \hspace{0.05cm}.$$
- The loss compared to the redundancy-free binary system is thus almost $8 \, {\rm dB}$.
- The reason for this serious loss of signal-to-noise ratio is that with the AMI code, despite $37\%$ redundancy, the symbol sequence $\text{ ...} , \, –1, \, +1, \, –1, \text{ ...} $ which is particularly unfavorable with respect to intersymbol interference, is not excluded.
(3) The threshold $E_2$ must be in the middle between $d_{\rm top}$ and $d_{\rm bottom}$:
- $$E_2= {1}/{2} \cdot (d_{\rm top} + d_{\rm bottom}) = {1}/{2} \cdot (g_0 - g_1 ) \hspace{0.15cm}\underline {= 0.67\,{\rm V}}\hspace{0.05cm}.$$
The threshold value $E_1$ is symmetrical to this: $E_1 \, \underline {= \, –0.67 {\rm V}}$.
(4) We again assume the same basic pulse values.
- The worst-case sequence with respect to the upper boundary line of the upper eye is $\text{ ...} , 0, \, +1, \, 0, \text{ ...} $,
- while the lower boundary line is defined by $\text{ ...} , 0, \, 0, \, +1, \text{ ...} $ or $\text{ ...} , +1, \, 0, \, 0, \text{ ...} $ respectively.
- From this follows:
- $$d_{\rm top}= g_0, \hspace{0.2cm} d_{\rm bottom} = g_1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{2} = {g_0}/{2} - {g_1}/{2}\hspace{0.15cm}\underline { = 0.667\,{\rm V}} \hspace{0.05cm}.$$
(5) Using the result from (4), we obtain analogous to subtask (2):
- $$\rho_{\rm U} = \frac{(0.67\,{\rm V})^2}{(0.2\,{\rm V})^2} = 11.2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 10.5\,{\rm dB}} \hspace{0.05cm}.$$
- Prerequisite for this result are thresholds at
- $$E_2= {1}/{2} \cdot (g_0 + g_1 ) = 0.89\,{\rm V}, \hspace{0.2cm}E_1 = - 0.89\,{\rm V}\hspace{0.05cm}.$$
- It should be noted that the same cutoff frequency $f_{\rm G} \cdot T = 0.5$ was always assumed here.
- If the cutoff frequency is optimized, it may well be that the duobinary code is superior to the redundancy-free binary code if the characteristic cable attenuation is sufficiently large.
