Examples of Binary Block Codes

1. Channel Coding
2. Binary Block Codes for Channel Coding
3. Examples of Binary Block Codes

• Previous page
• Next page

• Previous page
• Next page

Single Parity Check Codes

The  Single Parity Check Code  (SPC) adds to the information block  $\underline{u}= (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$  a parity bit $p$ :

Various single parity check codes  $(n = k + 1)$

$$\underline{u} = (u_1, u_2,\hspace{0.05cm} \text{...} \hspace{0.05cm} , u_k) \hspace{0.3cm}$$

$$\Rightarrow \hspace{0.3cm} \underline{x} = (x_1, x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm} , x_n) = (u_1, u_2,\hspace{0.05cm} \text{...}\hspace{0.05cm} , u_k, p) \hspace{0.05cm}.$$

The graphic shows three coding examples:

• $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 4 \ (k = 2)$,

• $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 8 \ (k = 3)$,

• $|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 16 \ (k = 4)$.

This very simple code can be characterized as follows:

• From  $n = k + 1$  follows for the  code rate  $R = k/n = (n-1)/n$  and for the  redundancy  $1-R = 1/n$. For  $k = 2$ , for example, the code rate is  $2/3$  and the relative redundancy is  $33.3\%$.

• The parity bit is obtained by modulo–2–addition. This is the addition in the  Galois field  to the base  $2$   ⇒   $\rm GF(2)$, so that  $1 \oplus 1 = 0$  results:

$$p = u_1 \oplus u_2 \oplus \text{...} \hspace{0.05cm} \oplus u_k \hspace{0.05cm}.$$

• Thus every valid codeword  $\underline{x}$  contains an even number of ones. Expressed as  $\oplus$  or in simplified notation according to the second equation, this condition reads:

$$x_1 \oplus x_2 \oplus \text{...} \hspace{0.05cm} \oplus x_n = 0 \hspace{0.05cm}, \hspace{0.5cm}{\rm or:}\hspace{0.5cm} \sum_{i=1}^{n} \hspace{0.2cm} x_i = 0\hspace{0.05cm} , \hspace{0.3cm} {\rm Addition\hspace{0.15cm} in \hspace{0.15cm} GF(2)} \hspace{0.05cm}.$$

• For  $k = 2$   ⇒   $n = 3$  the following four code words result, where the parity bit  $p$  is marked by a small arrow in each case:

$$\underline{x}_0 = (0, 0_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 1_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_2 = (1, 0 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_3 = (1, 1 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}.$$

• This code  $\mathcal{C} = \big \{ (0, 0, 0), \ (0, 1, 1), \ (1, 0, 1), \ (1, 1, 0) \big \}$  is  linear since the sum of any two codewords again gives a valid codeword, for example.

$$\underline{x}_1 \oplus \underline{x}_2 = \underline{x}_3.$$

• For any  $k$   ⇒   $n = k+1$  each codeword differs from all others at an even number of positions. Thus, the minimum distance of the code is 

$$d_{\rm min} = 2.$$

$\text{Definition:}$  Each  $\text{Single Parity Check Code (SPC)}$  can be formally described as follows:

$$\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{-0.15cm}: \hspace{0.15cm}{\rm with \hspace{0.15cm}even\hspace{0.15cm} number\hspace{0.15cm} of\hspace{0.15cm} ones\hspace{0.15cm} in \hspace{0.15cm} } \underline{x} \}\hspace{0.05cm}.$$

• With the general code name  $(n, \ k, \ d_{\rm min})$  any Single Parity–check Code can also be named  $\text{SPC }(n, \ n-1, \ 2)$ .
• The top graph thus shows the  $\text{SPC (3, 2, 2)}$, the  $\text{SPC (4, 3, 2)}$, and the  $\text{SPC (5, 4, 2)}$.

The digital channel may change the codeword  $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$  to the receive word  $\underline{y}= (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$. With the error vector  $\underline{e}= (e_1, e_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, e_n)$  holds:

$$\underline{y}= \underline{x} \oplus \underline{e}.$$

For decoding the Single Parity Check Code one forms the so-called  syndrome:

$$s = y_1 \oplus y_2 \oplus \hspace{0.05cm}\text{...} \hspace{0.05cm} \oplus y_n = \sum_{i=1}^{n} \hspace{0.2cm} y_i \hspace{0.1cm} \in \hspace{0.2cm} \{0, 1 \} \hspace{0.05cm}.$$

The result  $s=1$  then indicates (at least) one bit error within the codeword, while  $s=0$  should be interpreted as follows:

• The transmission was error-free, or:
  
• The number of bit errors is even.
  
  

Possible received values at the $\text{SPC (4, 3, 2)}$

$\text{Example 1:}$  We consider the  $\text{SPC (4, 3, 2)}$  and assume that the null word was sent. The table shows all possibilities that  $f$  bits are corrupted and gives the respective syndrome  $s \in \{0, 1\}$ .

For the  BSC model  with the crossover probability (Noah)  $\varepsilon = 1\%$  the following probabilities then result:

• The information word is correctly decoded (blue background):

$${\rm Pr}(\underline{v} = \underline{u}) = {\rm Pr}(\underline{y} = \underline{x}) = (1 - \varepsilon)^n = 0.99^4 \approx 96\,\%\hspace{0.05cm}.$$

• The decoder detects that transmission errors have occurred (green background):

$${\rm Pr}(s=1) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=1 \atop f \hspace{0.1cm}{\rm ungerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = {4 \choose 1} \cdot 0.01 \cdot 0.99^3 + {4 \choose 3} \cdot 0.01^3 \cdot 0.99 \approx 3.9\,\%\hspace{0.05cm}.$$

• The information word is decoded incorrectly (red background):

$${\rm Pr}(\underline{v} \ne \underline{u}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=2 \atop f \hspace{0.1cm}{\rm gerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = 1 - {\rm Pr}(\underline{v} = \underline{u}) - {\rm Pr}(s=1)\approx 0.1\,\%\hspace{0.05cm}.$$

We refer here to the interactive applet  Binomial and Poisson Distribution. The results obtained here are also discussed again in the  Exercise A1.5 

$\text{Example 2:}$  Error correction of the single parity–check code is not possible for the BSC–model unlike the  BEC–channel  (Binary Erasure Channel).

Bit errors are excluded with this one. If only one bit is erased $($  erasure,  $\rm E)$, then due to the fact "the number of ones in the codeword is even" error correction is also possible, for example for the  $\text{SPC (5, 4, 2)}$:

$$\underline{y} = (1, 0, {\rm E}, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (1, 0, 1, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (1, 0, 1, 1) = \underline{u}\hspace{0.05cm},$$ $$\underline{y}=(0, 1, 1, {\rm E}, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 1, 0, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 1, 0) = \underline{u}\hspace{0.05cm},$$ $$\underline{y} = (0, 1, 0, 1, {\rm E}) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 0, 1, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 0, 1) = \underline{u}\hspace{0.05cm}.$$

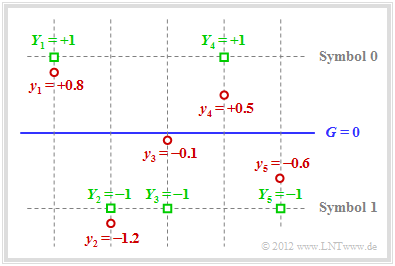
$\text{Example 3:}$  Also with  AWGN channel  error correction is possible when applying  Soft Decision . For the following we assume bipolar signaling:

To clarify "soft decision" at AWGN

• $x=0$   ⇒   $\tilde{x}= +1$, as well as
• $x=1$   ⇒   $\tilde{x}= -1$.
  

The graphic illustrates the facts presented here:

• For example, the receive vector is (red dots):

$$\underline{y} = (+0.8, -1.2, -0.1, +0.5, -0.6) \hspace{0.05cm}.$$

• With a hard decision (threshold  $G = 0$, only the signs are evaluated) one would arrive at the following binary result $($green squares  $Y_i = y_i/ \vert y_i \vert)$:

$$\underline{Y} = (+1, -1, -1, +1, -1) \hspace{0.05cm}.$$

• In symbol notation, this gives  $(0, 1, 1, 0, 1)$, which is not a valid codeword of  $\text{SPC (5, 4, 2)}$  ⇒   syndrome  $s = 1$. So one, three or five bits must have been corrupted.
  

• The probability for three or five bit errors, however, is orders of magnitude smaller than that for a single error. The assumption of "one bit error" is therefore not unreasonable.
  

• Since the received value  $y_3$  is very close to the threshold  $G = 0$  it is assumed that exactly this bit has been corrupted.

• Thus, in Soft Decision, the decision is for  $\underline{z} = (0, 1, 0, 0, 1)$   ⇒   $\underline{v} = (0, 1, 0, 0)$.
• The block error probability  ${\rm Pr}(\underline{v} \ne \underline{u})$  is thus lowest.

Repetition Codes

$\text{Definition:}$  A  $\text{repetition code}$  ($\rm RC)$  is a linear binary  $(n, \, k)$–block code of the form

$$\mathcal{C} = \big \{ \underline{x} \in {\rm GF}(2^n)\text{:} \ \ x_i = x_j \hspace{0.15cm}{\rm for \hspace{0.15cm}all\hspace{0.25cm} } i, j = 1, \hspace{0.05cm} \text{...} \hspace{0.05cm}, n \big \}.$$

• The code parameter  $n$  denotes the code length. Independent of  $n$  always holds  $k = 1$.
• Accordingly, there exist only the two codewords  $(0, 0, \hspace{0.05cm} \text{...} \hspace{0.05cm} , 0)$  and  $(1, 1, \hspace{0.05cm}\text{...}\hspace{0.05cm} , 1)$, which differ in  $n$  binary places.
• From this follows for the minimum distance  $d_{\rm min} = n$.

Various (Repetition Codes)

The graphic shows repetition codes for

• $n=3$,
• $n=4$,
• $n=5$.

Such a repetition code has the following properties:

• This  $(n, \, 1, \, n)$–block code has the very small code rate  $R = 1/n$, so it is only suitable for transferring or storing small files.
• On the other hand, the repetition code is very robust.
• In particular, in the  BEC channel  (Binary Erasure Channel), a single correctly transmitted bit at any position (all other bits may be erased) is sufficient to correctly decode the information word.
  

$\text{Example 4: Decoding and error probabilities at the BSC channel.}$

The  BSC channel  with $\varepsilon = 10\%$ applies. The decoding is based on the majority principle.

• For odd  $n$ , $e=n-1$ bit errors can be detected and  $t=(n-1)/2$  bit errors can be corrected. This gives $u$ for the probability of correct decoding of the information bits :

$${\rm Pr}(v = u) = \sum_{f=0 }^{(n-1)/2} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} \hspace{0.05cm}.$$

• The following numerical values are valid for  $n = 5$. That means:   There are  $t = 2$  Bit errors correctable:

$${\rm Pr}(v = u) = (1 - \varepsilon)^5 + 5 \cdot \varepsilon \cdot (1 - \varepsilon)^4 + 10 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^3 \approx 99.15\,\%$$

$$\Rightarrow\hspace{0.3cm}{\rm Pr}(v \ne u) = 1- {\rm Pr}(v = u) \approx 0.85\,\%\hspace{0.05cm}.$$

• On the other hand, with even  $n$  only  $t=n/2-1$  errors can be corrected. If  $n$  is increased from  $5$  to  $6$, then only two bit errors within a codeword can be corrected. A third bit error cannot be corrected, but at least it can be recognized:

$${\rm Pr}({\rm not\hspace{0.15cm} correctable\hspace{0.15cm} error}) = {6 \choose 3} \cdot \varepsilon^{3} \cdot (1 - \varepsilon)^{3}= 20 \cdot 0.1^{3} \cdot 0.9^{3}\approx 1.46\,\%\hspace{0.05cm}.$$

• An (undetected) decoding error  $(v \ne u)$  results only when four or more bits have been corrupted within the 6 bit–word. As an approximation, assuming that five or six bit errors are much less likely than four:

$${\rm Pr}(v \ne u) \approx {6 \choose 4} \cdot \varepsilon^{4} \cdot (1 - \varepsilon)^{2}= 0.122\,\%\hspace{0.05cm}.$$

• It is interesting to note that for  $\text{RC(6, 1, 6)}$  the probability  ${\rm Pr}(v = u)$  for a possible and correct decoding with  $98.42\%$  is smaller than for  $\text{RC (5, 1, 5)}$. For the latter:

$${\rm Pr}(v = u) = 1- 0.00122 \approx 99.88\%.$$

$\text{Example 5: Performance of the repetition code at the AWGN channel.}$

We now consider the  AWGN channel. For uncoded transmission $($or the repeat code with  $n=1)$  the received value is  $y = \tilde{x}+\eta$, where  $\tilde{x} \in \{+1, -1\}$ denotes the information bit in bipolar signaling and  $\eta$  denotes the noise term. To avoid confusion with the code parameter  $n$  we have renamed the noise:   $n → \eta$.

For the error probability, with the  complementary Gaussian error integral  ${\rm Q}(x)$

$${\rm Pr}(v \ne u) = {\rm Q}(\sqrt{\rho}) \hspace{0.05cm},$$

where the following physical quantities are to be used:

• the SNR  $\rho= 1/\sigma^2 = 2 \cdot E_{\rm S}/N_0$,
  

• the energy  $E_{\rm S}$  per code symbol   ⇒   "symbol energy",
  

• the normalized standard deviation  $\sigma$  of the noise, valid for the bipolar information bit  $\tilde{x} \in \{+1, -1\}$, and
  

• The constant (one-sided) noise power density  $N_0$  of the AWGN–noise.
  
  

In contrast, for a  $(n, 1, n)$–repetition code, the input value of the maximum likelihood decoder  $y \hspace{0.04cm}' = \tilde{x} \hspace{0.04cm}'+\eta \hspace{0.04cm}'$  with the following properties:

Error probability of the repetition code at the AWGN channel

$$\tilde{x} \hspace{0.04cm}' =\sum_{i=1 }^{n} \tilde{x}_i \in \{ +n, -n \}\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fold \hspace{0.15cm}amplitude}$$

$$\hspace{4.8cm} \Rightarrow\hspace{0.2cm}n^2{\rm -fold \hspace{0.15cm}power}\hspace{0.05cm},$$

$$\eta\hspace{0.04cm}' = \sum_{i=1 }^{n} \eta_i\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fold \hspace{0.15cm}variance:\hspace{0.15cm} } \sigma^2 \rightarrow n \cdot \sigma^2\hspace{0.05cm},$$

$$\rho\hspace{0.04cm}' = \frac{n^2}{n \cdot \sigma^2} = n \cdot \rho \hspace{0.2cm} \Rightarrow\hspace{0.2cm}{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{n \cdot \frac{2E_{\rm S} }{N_0} } )\hspace{0.05cm}.$$

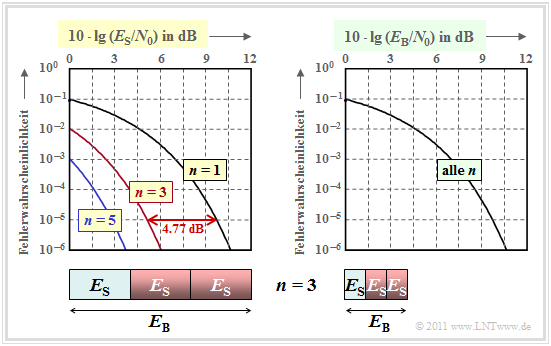
The error probability in double logarithmic representation is shown in the left graph. As abscissa is  $10 \cdot \lg \, (E_{\rm S}/N_0)$  plotted. The energy per bit  $(E_{\rm B})$  is  $n$  times larger than the symbol energy  $E_{\rm S}$, as illustrated in the graph for  $n=3$ .
This set of curves can be interpreted as follows:

• If one plots the error probability over the abscissa  $10 \cdot \lg \, (E_{\rm S}/N_0)$  then  $n$–times repetition over uncoded transmission  $(n=1)$  results in a significant improvement.
  

• The curve for the repetition factor  $n$  is obtained by left shifting by  $10 \cdot \lg \, n$  (in dB) with respect to the comparison curve. The gain is  $4.77 \ {\rm dB} \ (n = 3)$ or $\approx 5 \ {\rm dB} \ (n = 5)$.
  

• However, a comparison at constant  $E_{\rm S}$  is not fair, since with the repetition code  $\text{RC (5, 1, 5)}$  one spends a factor  $n$  larger energy for the transmission of an information bit than with uncoded transmission:   $E_{\rm B} = E_{\rm S}/{R} = n \cdot E_{\rm S}\hspace{0.05cm}.$

From the graph on the right, we can see that all the curves lie exactly on top of each other when plotted on the abscissa  $10 \cdot \lg \, (E_{\rm B}/N_0)$ 

$\text{Conclusion regarding repeat codes on the AWGN channel:}$

• The probability of error is independent of the repetition factor for a fair comparison  $n$:     ${\rm Pr}(v \ne u) = {\rm Q}\left (\sqrt{2E_{\rm B} /{N_0} } \right ) \hspace{0.05cm}.$

• For the AWGN channel, no  coding gain  can be achieved by a repeat code.

Hamming codes

Richard Wesley Hamming  hat 1962 eine Klasse binärer Blockcodes angegeben, die sich durch die Anzahl  $m = 2, 3, \text{...}$  der zugesetzten  Parity Bits  unterscheiden. Für diese Codeklasse gilt:

• Die Codelänge ergibt sich stets zu  $n = 2^m -1$. Möglich sind demzufolge beim Hamming–Code auch nur die Längen  $n = 3$,  $n = 7$,  $n = 15$,  $n = 31$,  $n = 63$,  $n = 127$,  $n = 255$, usw.
  

• Ein Informationswort besteht aus  $k = n-m$  Bit. Die Coderate ist somit gleich

$$R = \frac{k}{n} = \frac{2^m - 1 - m}{2^m - 1} \in \{1/3, \hspace{0.1cm}4/7,\hspace{0.1cm}11/15,\hspace{0.1cm}26/31,\hspace{0.1cm}57/63, \hspace{0.1cm}120/127,\hspace{0.1cm}247/255, \hspace{0.05cm} \text{...} \hspace{0.05cm} \}\hspace{0.05cm}.$$

• Alle Hamming–Codes weisen die minimale Distanz  $d_{\rm min} = 3$  auf. Bei größerer Codelänge  $n$  erreicht man  $d_{\rm min} = 3$  schon mit weniger Redundanz, also bei größerer Coderate  $R$.
  

• Aus der Angabe  $d_{\rm min} = 3$  folgt weiter, dass hier  $e = d_{\rm min} -1 =2$  Fehler erkannt werden können und man  $t = (d_{\rm min} -1)/2 = 1$  Fehler korrigieren kann.
  

• Der Hamming–Code  $\text{HC (3, 1, 3)}$  ist identisch mit dem Wiederholungscode  $\text{RP (3, 1, 3)}$  und lautet:

$$\mathcal{C} = \big \{ (0, 0, 0) \hspace{0.05cm}, (1, 1, 1) \big \}\hspace{0.05cm}.$$

• Bei systematischer Codierung sind die ersten  $k$  Stellen eines jeden Hamming–Codewortes  $\underline{x}$  identisch mit dem Informationswort  $\underline{u}$. Anschließend folgen dann die  $m = n-k$  Paritätsbit:

$$\underline{x} = ( x_1, x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) = ( u_1, u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_k, p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, p_{n-k}) \hspace{0.05cm}.$$

Verdeutlichung des $\text{(7, 4, 3)}$–Hamming–Codes

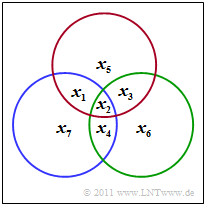
$\text{Beispiel 6: Paritätsgleichungen des (7, 4, 3)-Hamming-Codes}$
Der  $\text{(7, 4, 3)}$–Hamming–Code wird durch das dargestellte Schaubild verdeutlicht. Daraus kann man die drei Bedingungen ableiten:

$$x_1 \oplus x_2 \oplus x_3 \oplus x_5 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm},$$

$$x_2 \oplus x_3 \oplus x_4 \oplus x_6 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm},$$

$$x_1 \oplus x_2 \oplus x_4 \oplus x_7 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm}.$$

• Im Schaubild kennzeichnet der rote Kreis die erste Prüfgleichung, der grüne die zweite und der blaue die letzte.
• In jedem Kreis muss die Anzahl der Einsen geradzahlig sein.

Zuordnung $\underline{u} → \underline{x}$ des systematischen $\text{(7, 4, 3)}$–Hamming–Codes

Bei systematischer Codierung des  $\text{(7, 4, 3)}$–Hamming–Codes

$$x_1 = u_1 ,\hspace{0.2cm} x_2 = u_2 ,\hspace{0.2cm} x_3 = u_3 ,\hspace{0.2cm} x_4 = u_4 ,\hspace{0.2cm} x_5 = p_1 ,\hspace{0.2cm} x_6 = p_2 ,\hspace{0.2cm} x_7 = p_3$$

lauten die Bestimmungsgleichungen der drei Prüfbit, wie aus dem Schaubild hervorgeht:

$$p_1 =u_1 \oplus u_2 \oplus u_3 \hspace{0.05cm},$$

$$p_2 = u_2 \oplus u_3 \oplus u_4 \hspace{0.05cm},$$

$$p_3 = u_1 \oplus u_2 \oplus u_4 \hspace{0.05cm}.$$

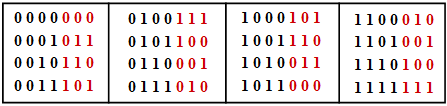
Die Tabelle zeigt die  $2^k = 16$  zulässigen Codeworte des systematischen  $\text{(7, 4, 3)}$–Codes:

$$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6, x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_3).$$

• Das Informationswort  $\underline{u} =( u_1, u_2, u_3, u_4)$  ist schwarz dargestellt und die Prüfbits  $p_1$,  $p_2$  und  $p_3$  rot.
• Man erkennt anhand dieser Tabelle, dass sich jeweils zwei der  $16$  möglichen Codeworte in mindestens  $d_{\rm min} = 3$  Binärwerten unterscheiden.

Später wird die  Decodierung linearer Blockcodes  noch ausführlich behandelt. Das folgende Beispiel soll die Decodierung des Hamming–Codes eher intuitiv erklären.

$\text{Beispiel 7: Paritätsgleichungen des (7, 4, 3)-Hamming-Codes}$

Wir gehen weiter vom systematischen  $\text{(7, 4, 3)}$–Code aus und betrachten das Empfangswort  $\underline{y} = ( y_1, y_2, y_3, y_4, y_5, y_6, y_7)$. Zur Decodierung bilden wir die drei Paritätsgleichungen

$$y_1 \oplus y_2 \oplus y_3 \oplus y_5 \hspace{-0.1cm}= \hspace{-0.1cm} 0 \hspace{0.05cm},\hspace{0.5cm}{\rm (I)}$$

$$y_2 \oplus y_3 \oplus y_4 \oplus y_6 \hspace{-0.1cm}= \hspace{-0.1cm}0 \hspace{0.05cm},\hspace{0.5cm}{\rm (II)}$$

$$y_1 \oplus y_2 \oplus y_4 \oplus y_7 \hspace{-0.1cm}= \hspace{-0.1cm} 0\hspace{0.05cm}. \hspace{0.5cm}{\rm (III)}$$

Unter der Voraussetzung, dass in jedem Codewort höchstens ein Bit verfälscht wird, gelten dann die folgenden Aussagen. Im Folgenden bezeichnet  $\underline{v}$  das Decodierergebnis; dieses sollte stets mit  $\underline{u} = (1, 0, 1, 0)$  übereinstimmen:

• Das Empfangswort  $\underline{y} = (1, 0, 1, 0, 0, 1, 1)$  erfüllt alle drei Paritätsgleichungen. Das heißt, dass kein einziger Übertragungsfehler aufgetreten ist   ⇒   $\underline{y} = \underline{x}$   ⇒   $\underline{v} = \underline{u} = (1, 0, 1, 0)$.
  

• Werden zwei der drei Paritätsgleichungen erfüllt wie zum Beispiel für das empfangene Wort  $\underline{y} =(1, 0, 1, 0, 0, 1, 0)$, so wurde ein Paritätsbit verfälscht und es gilt auch hier  $\underline{v} = \underline{u} = (1, 0, 1, 0)$.
  

• Mit  $\underline{y} = (1, 0, 1, 1, 0, 1, 1)$  wird nur die Gleichung  $\rm (I)$  erfüllt und die beiden anderen nicht. Somit kann man die Verfälschung des vierten Binärsymbols korrigieren, und es gilt auch hier  $\underline{v} = \underline{u} = (1, 0, 1, 0)$.
  

• Ein Übertragungsfehler des zweiten Bits   ⇒   $\underline{y} = (1, 1, 1, 0, 0, 1, 1)$  führt dazu, dass alle drei Paritätsgleichungen nicht erfüllt werden. Auch dieser Fehler lässt sich eindeutig korrigieren da nur  $u_2$  in allen Gleichungen vorkommt.

Aufgaben zum Kapitel

Aufgabe 1.5: SPC (5, 4) und BEC–Modell

Aufgabe 1.5Z: SPC (5, 4) vs. RC (5, 1)

Aufgabe 1.6: Zum (7, 4)–Hamming–Code