Exercise 1.1: For Labeling Books

• Return to book

ISBN–10? Or ISBN–13?

Since the 1960s,  all books are provided with a 10-digit  "International Standard Book Number"  $\rm (ISBN)$.  The last digit of this so-called  ISBN-10 specification  is calculated according to the following rule:

$$ z_{10}= \left ( \sum_{i=1}^{9} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.2cm} \mod 11 \hspace{0.05cm}.$$

Since 2007,  the specification according to the standard  ISBN-13  is additionally mandatory,  whereby the check digit  $z_{\rm 13}$  then results as follows:

$$z_{13} = 10 - \left ( \sum_{i=1}^{12} \hspace{0.2cm} z_i \cdot 3^{(i+1)\mod 2} \right ) \hspace{-0.2cm} \mod 10 \hspace{0.05cm}.$$

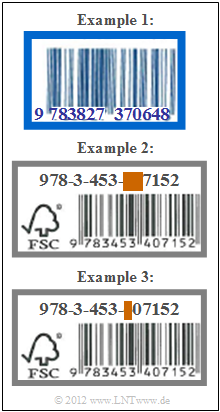
Some exemplary  "ISBNs"  are given opposite.  The following questions refer to these.

Hints:  This exercise belongs to the chapter  "Objective of Channel Coding"

Questions

1

What is the standard for  $\text{Example 1}$?

	ISBN-10,
	ISBN-13.

2

Accordingly  $\text{Example 2}$  two digits of an ISBN-13 are deleted.  Is it possible to reconstruct the ISBN?  If yes:   Specify the ISBN-13.

	Yes,
	No.

3

According to  $\text{Example 3}$  one digit of an ISBN-13 is erased.  Can the ISBN be reconstructed?  If Yes:   Specify the ISBN-13.

	Yes,
	No.

4

How many different values  $(M)$  can the check digit  $z_{\rm 10}$  take for ISBN-10?

$M \ = \ $ $\ \rm$

5

Assumed as ISBN-10 is  "3-8273-7064-7".  Which statement is true?

	This is not a valid ISBN.
	The ISBN could be correct.
	The ISBN is certainly correct.

Solution

Solution

(1)  Just by counting the ISBN digits,  you can tell that  answer 2  is correct.  The weighted sum over all digits is a multiple of 10:

$$S \ = \ \hspace{-0.1cm} \sum_{i=1}^{13} \hspace{0.2cm} z_i \cdot 3^{(i+1) \hspace{-0.2cm} \cdot 2} = (9+8+8+7+6+8) \cdot 1 + (7+3+2+3+0+4) \cdot 3 = 110\hspace{0.3cm} \Rightarrow \hspace{0.3cm} S \hspace{-0.2cm} \mod 10 \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$$

(2)  The answer is  No.  Only one cancellation can be reconstructed with a single check digit.

(3)  One digit can be reconstructed  ⇒   Yes.  For the digit  $z_{\rm 8}$,  it must hold:

$$[(9+8+4+3+0+1+2) \cdot 1 + (7+3+5+z_8+7+5) \cdot 3] \hspace{-0.2cm} \mod 10 = 0\hspace{0.3cm} \Rightarrow \hspace{0.3cm} [108 + 3z_8] \hspace{-0.2cm} \mod 10 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_8 \hspace{0.15cm}\underline {= 4} \hspace{0.05cm}.$$

(4)  By the modulo 11 operation,  $z_{10}$  can take the values  $0,\ 1,\ \text{...} ,\ 10$   ⇒   $\underline{M =11}$.

• Since  "10"  is not a digit,  one makes do with  $z_{10} = \rm X$.
• This corresponds to the Roman representation of the number  "10".

(5)  The test condition is:

$$\ \ S= \left ( \sum_{i=1}^{10} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.2cm} \mod 11 = 0 \hspace{0.05cm}.$$

• The given ISBN satisfies this condition:

$$3 \cdot 1 + 8 \cdot 2 + 2 \cdot 3 + 7 \cdot 4 + 3 \cdot 5 + 7 \cdot 6 + 0 \cdot 7 + 6 \cdot 8 + 4 \cdot 9 + 7 \cdot 10 = 264\hspace{0.3cm} ⇒\hspace{0.3cm} S= 264 \hspace{-0.3cm} \mod 11 = 0 \hspace{0.05cm}.$$

• Correct is  statement 2,  since the check sum  $S = 0$  could result even with more than one error.