Exercise 4.3: Different Frequencies
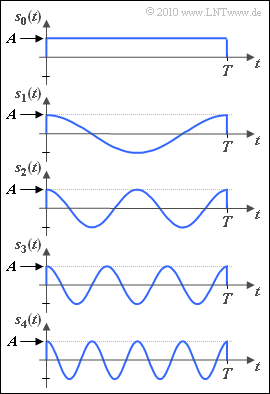
In the diagram $M = 5$ different signals $s_i(t)$ are shown. Contrary to the nomenclature in the theory section, the indexing variable $i$ can have the values $0, \ \text{...} \ , M-1$.
To be noted:
- All signals are time-limited to $0$ ... $T$; thus the energy of all signals is finite.
- The signal $s_1(t)$ has the period $T_0 = T$. The frequency is therefore $f_0 = 1/T$.
- The signals $s_i(t)$ with $i ≠ 0$ are cosine oscillations with frequency $i \cdot f_0$.
- In contrast, $s_0(t)$ is constant between $0$ and $T$.
- The maximum value of all signals is $A$ and $|s_i(t)| ≤ A$ holds.
In this exercise we are looking for the $N$ basis functions, which are numbered here with $j = 0, \ \text{...} \ , N-1$.
Note: The exercise belongs to the chapter "Signals, Basis Functions and Vector Spaces".
Question
Solution
- This takes into account the different frequencies and the limitation to the range $0 ≤ t < T$.
- The signals $s_i(t)$ according to suggestion 3, on the other hand, do not differ with respect to frequency, but have different phase positions.
(2) The energy-limited signals $s_i(t) = A \cdot \cos {(2\pi \cdot i \cdot t/T)}$ are all orthogonal to each other, that is, the inner product of two signals $s_i(t)$ and $s_k(t)$ with $i ≠ k$ is always $0$:
- $$< \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} A^2 \cdot \int_{0}^{T}\cos(2\pi \cdot i \cdot t/T) \cdot \cos(2\pi \cdot k \cdot t/T)\,{\rm d} t $$
- $$ \Rightarrow \hspace{0.3cm} < \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} {A^2}/{2} \cdot \int_{0}^{T}\cos(2\pi (i-k) t/T) \,{\rm d} t + \frac{A^2}{2} \cdot \int_{0}^{T}\cos(2\pi (i+k) t/T) \,{\rm d} t \hspace{0.05cm}.$$
- With $i ∈ \{0, \ \text{...} \ , 4\}$ and $k ∈ \{0, \ \text{...}\ , 4\}$ as well as $i ≠ j$, both $i \, – k$ is integer not equal to $0$, as is the sum $i + k$.
- Thus, both integrals yield the result zero:
- $$< \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm}= 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.05cm}\hspace{0.15cm}\underline {N = M = 5} \hspace{0.05cm}.$$
(3) The energy of the signal $s_0(t)$, which is constant within $T$, is equal to
- $$E_0 = ||s_0(t)||^2 = A^2 \cdot T \hspace{0.3cm}\Rightarrow \hspace{0.3cm} ||s_0(t)|| = A \cdot \sqrt{T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_0 (t) = \frac{s_0(t)}{||s_0(t)||} = \left\{ \begin{array}{c} 1/\sqrt{T} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$
Therefore, solution 2 is correct.
(4) The last solution is correct because of
- $$E_1 = ||s_1(t)||^2 = \frac{A^2 \cdot T}{2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} ||s_1(t)|| = A \cdot \sqrt{{T}/{2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_1 (t) = \frac{s_1(t)}{||s_1(t)||} = \left\{ \begin{array}{c} \sqrt{2/T} \cdot \cos(2\pi t/T) \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$