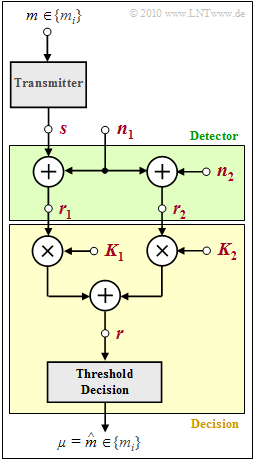
Exercise 4.5: Irrelevance Theorem

Considered optimal system with "detector" and "decision"

The communication system given by the graph is to be investigated. The binary message $m ∈ \{m_0, m_1\}$ with equal occurrence probabilities

$${\rm Pr} (m_0 ) = {\rm Pr} (m_1 ) = 0.5$$

is represented by the two signals

$$s_0 = \sqrt{E_s} \hspace{0.05cm},\hspace{0.2cm}s_1 = -\sqrt{E_s}$$

where the assignments $m_0 ⇔ s_0$ and $m_1 ⇔ s_1$ are one-to-one.

The detector $($highlighted in green in the figure$)$ provides two decision values

$$r_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} s + n_1\hspace{0.05cm},$$

$$r_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} n_1 + n_2\hspace{0.05cm},$$

from which the decision forms the estimated values $\mu ∈ \{m_0,\ m_1\}$ for the transmitted message $m$. The decision includes

two weighting factors $K_1$ and $K_2$,

a summation point, and

a threshold decision with the threshold at $0$.

Three evaluations are considered in this exercises:

Decision based on $r_1$ $(K_1 ≠ 0,\ K_2 = 0)$,
decision based on $r_2$ $(K_1 = 0,\ K_2 ≠ 0)$,
joint evaluation of $r_1$ und $r_2$ $(K_1 ≠ 0,\ K_2 ≠ 0)$.

Notes:

The exercise belongs to the chapter "Structure of the Optimal Receiver" of this book.

In particular, "the irrelevance theorem" is referred to here, but besides that also the "Optimal receiver for the AWGN channel".

For more information on topics relevant to this exercise, see the following links:

For the error probability of a system $r = s + n$ $($because of $N = 1$ here $s,\ n,\ r$ are scalars$)$ is valid:

$$p_{\rm S} = {\rm Pr} ({\rm symbol\ \ error} ) = {\rm Q} \left ( \sqrt{{2 E_s}/{N_0}}\right ) \hspace{0.05cm},$$

where a binary message signal $s ∈ \{s_0,\ s_1\}$ with $s_0 = \sqrt{E_s} \hspace{0.05cm},\hspace{0.2cm}s_1 = -\sqrt{E_s}$ is assumed.

Let the two noise sources $n_1$ and $n_2$ be independent of each other and also independent of the transmitted signal $s ∈ \{s_0,\ s_1\}$.

$n_1$ and $n_2$ can each be modeled by AWGN noise sources $($white, Gaussian distributed, mean-free, variance $\sigma^2 = N_0/2)$.

For numerical calculations, use the values

$$E_s = 8 \cdot 10^{-6}\,{\rm Ws}\hspace{0.05cm},\hspace{0.2cm}N_0 = 10^{-6}\,{\rm W/Hz} \hspace{0.05cm}.$$

The "complementary Gaussian error function" gives the following results:

$${\rm Q}(0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5\hspace{0.05cm},\hspace{1.35cm}{\rm Q}(2^{0.5}) = 0.786 \cdot 10^{-1}\hspace{0.05cm},\hspace{1.1cm}{\rm Q}(2) = 0.227 \cdot 10^{-1}\hspace{0.05cm},$$

$${\rm Q}(2 \cdot 2^{0.5}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.234 \cdot 10^{-2}\hspace{0.05cm},\hspace{0.2cm}{\rm Q}(4) = 0.317 \cdot 10^{-4} \hspace{0.05cm},\hspace{0.2cm}{\rm Q}(4 \cdot 2^{0.5}) = 0.771 \cdot 10^{-8}\hspace{0.05cm}.$$

Questions

	The ML receiver is better than the MAP receiver.
	The MAP receiver is better than the ML receiver.
	Both receivers deliver the same result.

${\rm Pr(symbol\hspace{0.15cm} error)}\ = \ $

$\ \%$

${\rm Pr(symbol\hspace{0.15cm}error)}\ = \ $

$\ \%$

	Yes.
	No.

	$\mu = {\rm arg \ min} \, \big[(\rho_1 + \rho_2) \cdot s_i \big]$,
	$\mu = {\rm arg \ min} \, \big[(\rho_2 \, - 2 \rho_1) \cdot s_i \big]$,
	$\mu = {\rm arg \ max} \, \big[(\rho_1 - \rho_2/2) \cdot s_i \big]$.

$K_2 \ = \ $

${\rm Minimum \ \big[Pr(symbol\hspace{0.15cm}error)\big]} \ = \ $

$\ \cdot 10^{\rm -8}$

Solution

(1) The last alternative solution is correct:

In general, the MAP receiver leads to a smaller error probability.
However, if the occurrence probabilities ${\rm Pr}(m = m_0) = {\rm Pr}(m = m_1) = 0.5$ are equal, both receivers yield the same result.

(2) With $K_2 = 0$ and $K_1 = 1$ the result is

$$r = r_1 = s + n_1\hspace{0.05cm}.$$

With bipolar (antipodal) transmitted signal and AWGN noise, the error probability of the optimal receiver (whether implemented as a correlation or matched filter receiver) is equal to

$$p_{\rm S} = {\rm Pr} ({\rm symbol error} ) = {\rm Q} \left ( \sqrt{ E_s /{\sigma}}\right ) = {\rm Q} \left ( \sqrt{2 E_s /N_0}\right ) \hspace{0.05cm}.$$

With $E_s = 8 \cdot 10^{\rm –6} \ \rm Ws$ and $N_0 = 10^{\rm –6} \ \rm W/Hz$, we further obtain:

$$p_{\rm S} = {\rm Pr} ({\rm symbol error} ) = {\rm Q} \left ( \sqrt{\frac{2 \cdot 8 \cdot 10^{-6}\,{\rm Ws}}{10^{-6}\,{\rm W/Hz} }}\right ) = {\rm Q} (4) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.00317 \%}\hspace{0.05cm}.$$

This result is independent of $K_1$, since amplification or attenuation changes the useful power in the same way as the noise power.

(3) With $K_1 = 0$ and $K_2 = 1$, the decision variable is:

$$r = r_2 = n_1 + n_2\hspace{0.05cm}.$$

This contains no information about the useful signal, only noise, and it holds independently of $K_2$:

$$p_{\rm S} = {\rm Pr} ({\rm symbol error} ) = {\rm Q} (0) \hspace{0.15cm}\underline {= 50\%} \hspace{0.05cm}.$$

(4) Because of ${\rm Pr}(m = m_0) = {\rm Pr}(m = m_1)$, the decision rule of the optimal receiver (whether realized as MAP or as ML) is:

$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ p_{m \hspace{0.05cm}|\hspace{0.05cm}r_1, \hspace{0.05cm}r_2 } \hspace{0.05cm} (m_i \hspace{0.05cm}|\hspace{0.05cm}\rho_1, \hspace{0.05cm}\rho_2 ) ] = {\rm arg} \max_i \hspace{0.1cm} [ p_{r_1, \hspace{0.05cm}r_2 \hspace{0.05cm}|\hspace{0.05cm} m} \hspace{0.05cm} ( \rho_1, \hspace{0.05cm}\rho_2 \hspace{0.05cm}|\hspace{0.05cm} m_i ) \cdot {\rm Pr} (m = m_i)] = {\rm arg} \max_i \hspace{0.1cm} [ p_{r_1, \hspace{0.05cm}r_2 \hspace{0.05cm}|\hspace{0.05cm} s} \hspace{0.05cm} ( \rho_1, \hspace{0.05cm}\rho_2 \hspace{0.05cm}|\hspace{0.05cm} s_i ) ] \hspace{0.05cm}.$$

This composite probability density can be rewritten as follows:

$$\hat{m} ={\rm arg} \max_i \hspace{0.1cm} [ p_{r_1 \hspace{0.05cm}|\hspace{0.05cm} s} \hspace{0.05cm} ( \rho_1 \hspace{0.05cm}|\hspace{0.05cm} s_i ) \cdot p_{r_2 \hspace{0.05cm}|\hspace{0.05cm} r_1, \hspace{0.05cm}s} \hspace{0.05cm} ( \rho_2 \hspace{0.05cm}|\hspace{0.05cm} \rho_1, \hspace{0.05cm}s_i ) ] \hspace{0.05cm}.$$

Now, since the second multiplicand also depends on the message ($s_i$), $r_2$ should definitely be included in the decision process. Thus, the correct answer is: YES.

(5) For AWGN noise with variance $\sigma^2$, the two composite densities introduced in (4) together with their product $P$ give:

$$p_{r_1\hspace{0.05cm}|\hspace{0.05cm} s}(\rho_1\hspace{0.05cm}|\hspace{0.05cm}s_i) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi} \cdot \sigma}\cdot {\rm exp} \left [ - \frac{(\rho_1 - s_i)^2}{2 \sigma^2}\right ]\hspace{0.05cm},\hspace{1cm} p_{r_2\hspace{0.05cm}|\hspace{0.05cm}r_1,\hspace{0.05cm} s}(\rho_2\hspace{0.05cm}|\hspace{0.05cm}\rho_1, \hspace{0.05cm}s_i) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi} \cdot \sigma}\cdot {\rm exp} \left [ - \frac{(\rho_2 - (\rho_1 - s_i))^2}{2 \sigma^2}\right ]\hspace{0.05cm}$$

$$ \Rightarrow \hspace{0.3cm} P \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{{2\pi} \cdot \sigma^2}\cdot {\rm exp} \left [ - \frac{1}{2 \sigma^2} \cdot \left \{ (\rho_1 - s_i)^2 + (\rho_2 - (\rho_1 - s_i))^2\right \}\right ]\hspace{0.05cm}.$$

We are looking for the argument that maximizes this product $P$, which at the same time means that the expression in the curly brackets should take the smallest possible value:

$$\mu = \hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm arg} \max_i \hspace{0.1cm} P = {\rm arg} \min _i \hspace{0.1cm} \left \{ (\rho_1 - s_i)^2 + (\rho_2 - (\rho_1 - s_i))^2\right \} $$

$$\Rightarrow \hspace{0.3cm} \mu = \hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm arg} \min _i \hspace{0.1cm}\left \{ \rho_1^2 - 2\rho_1 s_i + s_i^2 + \rho_2^2 - 2\rho_1 \rho_2 + 2\rho_2 s_i+ \rho_1^2 - 2\rho_1 s_i + s_i^2\right \} \hspace{0.05cm}.$$

Here $\mu$ denotes the estimated value of the message. In this minimization, all terms that do not depend on the message $s_i$ can now be omitted. Likewise, the terms $s_i^2$ are disregarded, since $s_0^2 = s_1^2$ holds. Thus, the much simpler decision rule is obtained:

$$\mu = {\rm arg} \min _i \hspace{0.1cm}\left \{ - 4\rho_1 s_i + 2\rho_2 s_i \right \}={\rm arg} \min _i \hspace{0.1cm}\left \{ (\rho_2 - 2\rho_1) \cdot s_i \right \} \hspace{0.05cm}.$$

So, correct is already the proposed solution 2. But after multiplication by $–1/2$, we also get the last mentioned decision rule:

$$\mu = {\rm arg} \max_i \hspace{0.1cm}\left \{ (\rho_1 - \rho_2/2) \cdot s_i \right \} \hspace{0.05cm}.$$

Thus, the solutions 2 and 3.

(6) Setting $K_1 = 1$ and $\underline {K_2 = \, -0.5}$, the optimal decision rule with realization $\rho = \rho_1 \, – \rho_2/2$ is:

$$\mu = \left\{ \begin{array}{c} m_0 \\ m_1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f{or}} \hspace{0.15cm} \rho > 0 \hspace{0.05cm}, \\ {\rm f{or}} \hspace{0.15cm} \rho < 0 \hspace{0.05cm}.\\ \end{array}$$

Since $\rho = 0$ only occurs with probability $0$, it does not matter in the sense of probability theory whether one assigns the message $\mu = m_0$ or $\mu = m_1$ to this event "$\rho = 0$".

(7) With $K_2 = \, -0.5$ one obtains for the input value of the decision:

$$r = r_1 - r_2/2 = s + n_1 - (n_1 + n_2)/2 = s + n \hspace{0.3cm} \Rightarrow \hspace{0.3cm} n = \frac{n_1 - n_2}{2}\hspace{0.05cm}.$$

The variance of this random variable is

$$\sigma_n^2 = {1}/{4} \cdot \left [ \sigma^2 + \sigma^2 \right ] = {\sigma^2}/{2}= {N_0}/{4}\hspace{0.05cm}.$$

From this, the error probability is analogous to subtask (2):

$${\rm Pr} ({\rm symbol error} ) = {\rm Q} \left ( \sqrt{\frac{E_s}{N_0/4}}\right ) = {\rm Q} \left ( 4 \cdot \sqrt{2}\right ) = {1}/{2} \cdot {\rm erfc}(4) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}} \hspace{0.05cm}.$$

Thus, by taking $r_2$ into account, the error probability can be lowered from $0.317 \cdot 10^{\rm –4}$ to the much smaller value of $0.771 \cdot 10^{-8}$, although the decision component $r_2$ contains only noise. However, this noise $r_2$ allows an estimate of the noise component $n_1$ of $r_1$.

Halving the transmit energy from $8 \cdot 10^{\rm –6} \ \rm Ws$ to $4 \cdot 10^{\rm –6} \ \rm Ws$, we still get the error probability $0.317 \cdot 10^{\rm –4}$ here, as calculated in subtask (2). When evaluating $r_1$ alone, on the other hand, the error probability would be $0.234 \cdot 10^{\rm –2}$.