Exercise 1.11Z: Syndrome Decoding again

Parity-check chart

The same constellation is considered as in "Exercise 1.11": The decoding of a $(7, 4, 3)$ Hamming code with the parity-check matrix

$${ \boldsymbol{\rm H}}_{\rm } = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$

Accordingly, the generator matrix is:

$${ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$

In "syndrome decoding" one forms from the received vector $\underline{y}$ the syndrome $\underline{s}$ according to the equation

$$\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} \in {\rm GF}(2^m) \hspace{0.05cm}.$$

With this result, any single error in the code word can be corrected in the Hamming code under consideration.

In the error-free case $\underline{s} = \underline{s}_{0} = (0, 0, 0)$.

But even three transmission errors may result in $\underline{s}_{0} = (0, 0, 0)$, so these errors remain undetected.

Hints:

The exercise belongs to the chapter "Decoding of Linear Block Codes".

For more information on syndrome decoding, see the specification sheet for "Exercise 1.11".

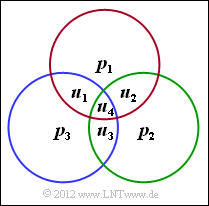
The graph illustrates the three parity-check equations corresponding to the parity-check matrix:
- first row: red circle,
- second row: green circle,
- third row: blue circle.

Questions

Solution

(1) The answer is YES, as can be seen from the given parity-check matrix $\mathbf{H}$:

This contains a $3×3$ diagonal matrix at the end.
The code words are therefore:

$$ \underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6, x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_{3}) \hspace{0.05cm}.$$

(2) With this received vector $\underline{y} = (1, 0, 0, 1, 0, 1, 0)$, all parity-check equations are satisfied:

$$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$

$$u_2 \oplus u_3 \oplus u_4 \oplus p_2 = 0 \oplus 0 \oplus 1 \oplus 1 = 0 \hspace{0.05cm},$$

$$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm}.$$

Accordingly, the correct answer is YES.

(3) It holds $\underline{s} = \underline{y} · \boldsymbol{\rm H}^{\rm T}$:

$$ \underline{s} = \begin{pmatrix} 1 &0 &0 &1 &0 &1 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 &0 &1\\ 1 &1 &0\\ 0 &1 &1\\ 1 &1 &1\\ 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} = \begin{pmatrix} 0 &0 &0 \end{pmatrix} = \underline{s}_0 \hspace{0.2cm} \Rightarrow\hspace{0.2cm} \hspace{0.15cm} \underline{ \rm Answer \hspace{0.15cm}1} \hspace{0.05cm}.$$

(4) One could now for each $\underline{y}$ check the equation $\underline{y} · \boldsymbol{\rm H}^{\rm T} = (0, 0, 0)$. Now here the result shall be obtained in a different way:

$\underline{y}= (1, 1, 0, 1, 0, 1, 0)$ differs from $\underline{y} = (1, 0, 0, 1, 0, 1, 0)$ in bit $u_{2}$, which is used only in the first two parity-check equations, but not in the last ⇒ $\underline{s} = \underline{s}_{6} = (1, 1, 0)$.

Applying the parity-check equations to $\underline{y} = (0, 1, 0, 1, 0, 0, 1)$, we obtain $\underline{s} = \underline{s}_{0} = (0, 0, 0)$, as evidenced by the following calculation:

$$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 0 \oplus 1 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$

$$u_2 \oplus u_3 \oplus u_4 \oplus p_2 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$

$$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 0 \oplus 0 \oplus 1 \oplus 1 = 0 \hspace{0.05cm}.$$

The same result is obtained with the received vector $\underline{y} = (0, 1, 1, 0, 1, 0, 1),$ which differs from the vector $(1, 0, 0, 1, 0, 1, 0)$ in all seven bit positions:

$$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 0 \oplus 1 \oplus 0 \oplus 1 = 0 \hspace{0.05cm},$$

$$u_2 \oplus u_3 \oplus u_4 \oplus p_2 = 1 \oplus 1 \oplus 0 \oplus 0 = 0 \hspace{0.05cm},$$

$$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 0 \oplus 1 \oplus 0 \oplus 1 = 0 \hspace{0.05cm}.$$

So the correct answers are answers 2 and 3.

	$\underline{s} = \underline{s}_{0} = (0, 0, 0),$
	$\underline{s} = \underline{s}_{3} = (0, 1, 1),$
	$\underline{s} = \underline{s}_{7} = (1, 1, 1).$

	$\underline{y} = (1, 1, 0, 1, 0, 1, 0),$
	$\underline{y} = (0, 1, 0, 1, 0, 0, 1),$
	$\underline{y} = (0, 1, 1, 0, 1, 0, 1).$

	Yes,
	No.

	Yes,
	No.