Exercise 1.16Z: Bounds for the Gaussian Error Function

• Return to book

${\rm Q}(x)$  and related functions

The probability that a zero mean Gaussian random variable  $n$  with standard deviation  $\sigma$   ⇒   variance  $\sigma^2$  is greater in amount than a given value  $A$ is equal to

$${\rm Pr}(n > A) = {\rm Pr}(n < -A) ={\rm Q}(A/\sigma) \hspace{0.05cm}.$$

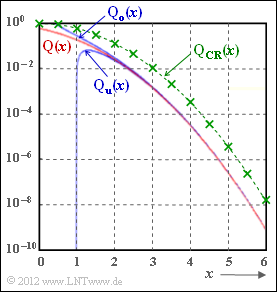
Here is used one of the most important functions for communications engineering (drawn in red in the diagram):  
the  "complementary Gaussian error function"

$${\rm Q} (x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u \hspace{0.05cm}.$$

${\rm Q}(x)$ is a monotonically decreasing function with ${\rm Q}(0) = 0.5$. For very large values of $x$, ${\rm Q}(x) tends \to 0$.

The integral of the ${\rm Q}$ function is not analytically solvable and is usually given in tabular form. From the literature, however, manageable approximations or bounds for positive $x$ values are known:

• the upper bound $($upper blue curve in adjacent graph, only valid for  $x > 0)$:

$$ {\rm Q_o}(x)=\frac{\rm 1}{\sqrt{\rm 2\pi}\cdot x}\cdot {\rm e}^{-x^{\rm 2}/\rm 2}\hspace{0.15cm} \ge \hspace{0.15cm} {\rm Q} (x) \hspace{0.05cm},$$

• the lower bound $($lower blue curve in the graph, only valid for  $x > 1)$:

$$ {\rm Q_u}(x)=\frac{\rm 1-{\rm 1}/{\it x^{\rm 2}}}{\sqrt{\rm 2\pi}\cdot x}\cdot \rm e^{-x^{\rm 2}/\rm 2} \hspace{0.15cm} \le \hspace{0.15cm} {\rm Q} (x) \hspace{0.05cm},$$

• the Chernoff-Rubin bound $($green curve in the graph, drawn for  $K = 1)$:

$${\rm Q_{CR}}(x)=K \cdot {\rm e}^{-x^{\rm 2}/\rm 2} \hspace{0.15cm} \ge \hspace{0.15cm} {\rm Q} (x) \hspace{0.05cm}.$$

In the exercise it is to be investigated to what extent these bounds can be used as approximations for  ${\rm Q}(x)$  and what corruptions result.

Hints:

• This exercise belongs to the chapter  block error probability bounds.
• Reference is also made to the chapter  Gaussian distributed random variables  in the book "Stochastic Signal Theory".
• The exercise also provides some important hints for solving  Exercise 1.16, in which the function  ${\rm Q}_{\rm CR}(x)$  is used to derive  Bhattacharyya barrier  is required for the AWGN channel.
• Further we refer to the interactive applet  Complementary Gaussian Error Functions.

Questions

1

Welche Werte liefern die obere und die untere Schranke für  $x = 4$?

${\rm Q_{o}}(x = 4) \ = \ $ $\ \cdot 10^{-5} $

${\rm Q_{u}}(x = 4) \ = \ $ $\ \cdot 10^{-5} $

2

Welche Aussagen gelten für die Funktionen  ${\rm Q_{o}}(x)$  und  ${\rm Q_{u}}(x)$?

	Für  $x ≥ 2$  sind die beiden Schranken brauchbar.
	Für  $x < 1$  ist  ${\rm Q_{u}}(x)$  unbrauchbar  $($wegen  ${\rm Q_{u}}(x)< 0)$.
	Für  $x < 1$  ist  ${\rm Q_{o}}(x)$  unbrauchbar  $($wegen  ${\rm Q_{o}}(x)> 1)$.

3

Um welchen Faktor liegt die Chernoff–Rubin–Schranke oberhalb von  ${\rm Q_{o}}(x)$?

${\rm Q}_{\rm CR}(x = 2)/{\rm Q_{o}}(x = 2 ) \ = \ $

${\rm Q}_{\rm CR}(x = 4)/{\rm Q_{o}}(x = 4 ) \ = \ $

${\rm Q}_{\rm CR}(x = 6)/{\rm Q_{o}}(x = 6 ) \ = \ $

4

Bestimmen Sie  $K$  so, dass  $K \cdot {\rm Q}_{\rm CR}(x)$  möglichst nahe bei  ${\rm Q}(x)$  liegt und gleichzeitig  ${\rm Q}(x) ≤ K · {\rm Q}_{\rm CR}(x)$  für alle  $x > 0$  eingehalten wird.

$K \ = \ $

Musterlösung

Solution

(1)  Die obere Schranke lautet:

$${\rm Q_o}(x)=\frac{1}{\sqrt{\rm 2\pi}\cdot x}\cdot {\rm e}^{-x^{\rm 2}/\rm 2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q_o}(4 )=\frac{1}{\sqrt{\rm 2\pi}\cdot 4}\cdot {\rm e}^{-8 }\hspace{0.15cm}\underline{\approx 3.346 \cdot 10^{-5}}\hspace{0.05cm}.$$

• Die untere Schranke kann wie folgt umgewandelt werden:

$${\rm Q_u}( x)=(1-1/x^2) \cdot {\rm Q_o}(x) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q_u}(4 ) \hspace{0.15cm}\underline{\approx 3.137 \cdot 10^{-5}} \hspace{0.05cm}.$$

• Die relativen Abweichungen gegenüber dem „echten” Wert ${\rm Q}(4) = 3.167 · 10^{–5}$ sind $+5\%$ bzw. $–1\%$.

(2)  Richtig sind die Lösungsvorschläge 1 und 2:

• Für $x = 2$ wird der tatsächliche Funktionswert ${\rm Q}(x) = 2.275 · 10^{–2}$ begrenzt durch ${\rm Q_{o}}(x) = 2.7 · 10^{–2}$ bzw. ${\rm Q_u}(x) = 2.025 · 10^{–2}$.
• Die relativen Abweichungen betragen demzufolge $18.7\%$ bzw. $–11\%.$
• Die letzte Aussage ist falsch:   Erst für $x < 0.37$ gilt ${\rm Q_o}(x) > 1.$

(3)  Für den Quotienten aus ${\rm Q}_{\rm CR}(x)$ und ${\rm Q_o}(x)$ gilt nach den vorgegebenen Gleichungen:

$$q(x) = \frac{{\rm Q_{CR}}(x)}{{\rm Q_{o}}(x)} = \frac{{\rm exp}(-x^2/2)}{{\rm exp}(-x^2/2)/({\sqrt{2\pi} \cdot x})} = {\sqrt{2\pi} \cdot x}$$

$$\Rightarrow \hspace{0.3cm} q(x) \approx 2.5 \cdot x \hspace{0.3cm} \Rightarrow \hspace{0.3cm} q(x =2) \hspace{0.15cm}\underline{=5}\hspace{0.05cm}, \hspace{0.2cm}q(x =4)\hspace{0.15cm}\underline{=10}\hspace{0.05cm}, \hspace{0.2cm}q(x =6) \hspace{0.15cm}\underline{=15}\hspace{0.05cm}.$$

• Je größer der Abszissenwert $x$ ist, um so ungenauer wird ${\rm Q}(x)$ durch ${\rm Q}_{\rm CR}(x)$ angenähert.
• Bei Betrachtung der Grafik auf der Angabenseite hat man (hatte ich) den Eindruck, dass ${\rm Q}_{\rm CR}(x)$ sich aus ${\rm Q}(x)$ durch Verschieben nach unten bzw. Verschieben nach oben ergibt. Das ist aber nur eine optische Täuschung und entspricht nicht dem Sachverhalt.

(4)  Mit $\underline{K = 0.5}$ stimmt die neue Schranke $0.5 · {\rm Q}_{\rm CR}(x)$ für $x = 0$ exakt mit ${\rm Q}(x=0) = 0.500$ überein.

• Für größere Abszissenwerte wird damit auch die Verfälschung $q \approx 1.25 · x$ nur halb so groß.