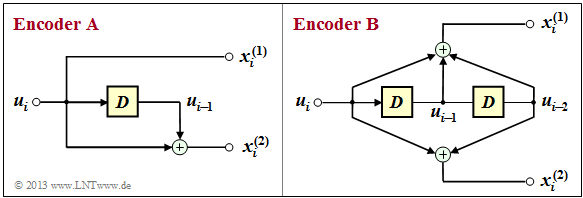
Exercise 3.1Z: Convolution Codes of Rate 1/2

Two convolutional codes of rate $1/2$

The graphic shows two convolutional encoders of rate $R = 1/2$. At the input there is the information sequence $\underline {u} = (u_1, u_2, \ \text{...} \ , u_i, \ \text{...})$ . From this, modulo 2 operations generate the two sequences

$$\underline{\it x}^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( \hspace{0.05cm}x_1^{(1)}\hspace{0.05cm},\hspace{0.05cm} x_2^{(1)}\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm},\hspace{0.05cm} x_i^{(1)} \hspace{0.05cm},\text{...} \hspace{0.05cm} \big )\hspace{0.05cm},$$

$$\underline{\it x}^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \big( \hspace{0.05cm}x_1^{(2)}\hspace{0.05cm},\hspace{0.05cm} x_2^{(2)}\hspace{0.05cm},\hspace{0.05cm}\text{...} \hspace{0.05cm},\hspace{0.05cm} x_i^{(2)} \hspace{0.05cm}, \text{...} \hspace{0.05cm} \big )$$

where $x_i^{(j)}$ with $j = 1$ resp. $j = 2$ except from $u_i$ also from the previous information bits $u_{i-1}, \ \text{...} \ , u_{i-m}$ may depend. One refers $m$ as the memory and $\nu = m + 1$ as the influence length of the code or the encoder. The considered coders $\rm A$ and $\rm B$ differ with respect to these quantities.

Hints:

The exercise refers to the chapter "Basics of Convolutional Coding".
Not shown in the diagram is the multiplexing of the two subsequences $\underline {x}^{(1)}$ and $\underline {x}^{(2)}$ to the resulting code sequence

$$\underline {x} = (x_1^{(1)}, x_1^{(2)}, x_2^{(1)}, x_2^{(2)}, \ \text{...}).$$

In subtasks (3) to (5) you are to determine the respective start of the sequences $\underline {x}^{(1)}, \underline{x}^{(2)}$ and $\underline{x}$ assuming the information sequence $\underline{u} = (1, 0, 1, 1, 0, 0, \ \text{. ..})$ is to be assumed.

Questions

Solution

(1) For both encoders, $k = 1$ and $n = 2$.

The memory $m$ and the influence length $\nu$ are different ⇒ Answers 3 and 4.

Equivalent coder representations

(2) The shift register of encoder $\rm A$ does contain two memory cells.

However, since $x_i^{(1)} = u_i$ and $x_i^{(2)} = u_i + u_{i-1}$ is influenced only by the immediately preceding bit $u_{i-1}$ besides the current information bit $u_i$, is

the memory $m = 1$, and
the influence length $\nu = m + 1 = 2$.

The graphic shows the two coders in another representation, whereby the "memory cells" are highlighted in yellow.

For the encoder $\rm A$ one recognizes only one such memory ⇒ $m = 1$.
In contrast, for the encoder $\rm B$ actually $m = 2$ and $\nu = 3$.
The proposed solution 2 is therefore correct.

(3) For the upper output of encoder $\rm B$ applies in general:

$$x_i^{(1)} = u_{i} + u_{i-1}+ u_{i-2} \hspace{0.05cm}.$$

Considering the preassignment ($u_0 = u_{-1} = 0$), we obtain with the above data:

$$x_1^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{1} + u_{0}+ u_{-1} = 1+0+0 = 1 \hspace{0.05cm},\hspace{1cm}x_2^{(1)} = u_{2} + u_{1}+ u_{0} = 0+1+0 = 1\hspace{0.05cm},$$

$$x_3^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{3} + u_{2}+ u_{1} \hspace{0.25cm}= 1+0+1 = 0 \hspace{0.05cm},\hspace{1cm}x_4^{(1)} = u_{4} + u_{3}+ u_{2} = 1+1+0 = 0\hspace{0.05cm},$$

$$x_5^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{5} + u_{4}+ u_{3} \hspace{0.25cm}= 0+1+1 = 0 \hspace{0.05cm},\hspace{1cm}x_6^{(1)} = u_{6} + u_{5}+ u_{4} = 0+0+1 = 1\hspace{0.05cm},$$

$$x_7^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} x_8^{(1)} = \text{...} \hspace{0.05cm}= 0 \hspace{0.05cm}.$$

The proposed solution 1 is therefore correct.
The second solution suggestion ⇒ $\underline {x}^{(1)} = $\underline {u}$ would only be valid for a systematic code (which is not present here). '''(4)''' Analogous to subtask (3), $x_i^{(2)} = u_i + u_{i–2}$ is obtained:

$$x_1^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1+0 = 1 \hspace{0.05cm},\hspace{0.2cm}x_2^{(2)} = 0+0 = 0\hspace{0.05cm}, \hspace{0.2cm}x_3^{(3)} = 1+1 = 0\hspace{0.05cm},\hspace{0.2cm}x_4^{(2)} = 1+0 = 1 \hspace{0.05cm},$$

$$x_5^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0+1 = 1\hspace{0.05cm}, \hspace{0.2cm}x_6^{(2)} = 0+1 = 1\hspace{0.05cm},\hspace{0.2cm} x_7^{(2)} = x_8^{(2)} = \text{...} \hspace{0.05cm}= 0 \hspace{0.05cm}.$$

The correct solution is therefore proposed solution 2.

(5) For the (entire) code sequence, one can formally write:

$$\underline{\it x} = \big( \hspace{0.05cm}\underline{\it x}_1\hspace{0.05cm}, \hspace{0.05cm} \underline{\it x}_2\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.05cm} \underline{\it x}_i \hspace{0.05cm}, \text{...} \hspace{0.05cm} \big )\hspace{0.05cm}, \hspace{0.3cm} \underline{\it x}_i = \big( x_i^{(1)}\hspace{0.05cm}, x_i^{(2)} \big) \hspace{0.4cm}\Rightarrow \hspace{0.4cm} \underline{\it x} = \big( \hspace{0.05cm}x_1^{(1)}\hspace{0.01cm},\hspace{0.05cm} x_2^{(1)}\hspace{0.01cm},\hspace{0.05cm} x_1^{(2)}\hspace{0.01cm},\hspace{0.05cm} x_2^{(2)}\hspace{0.01cm}, \hspace{0.05cm} \text{...} \hspace{0.05cm} \big )\hspace{0.05cm}. $$

A comparison with the solutions of exercises (3) and (4) shows the correctness of proposed solution 1.

	$k$: Number of information bits processed per coding step,
	$n$: Number of code bits output per coding step,
	$m$: memory order of the code or encoder,
	$\nu$: influence length of the code.

	$\underline {x}^{(1)} = (1, 1, 0, 0, 0, 1, 0, 0, \ ...)$,
	$\underline {x}^{(1)} = (1, 0, 1, 1, 0, 0, 0, 0, \ ...)$.

	$\underline{x}^{(2)} = (1, 1, 0, 0, 0, 1, 0, 0, \ \text{...})$,
	$\underline{x}^{(2)} = (1, 0, 0, 1, 1, 1, 0, 0, \ \text{...})$.

	$\underline {x} = (1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, \ \text{...})$,
	$\underline {x} = (1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, \ \text{...})$.

	Encoder $\rm A$,
	Encoder $\rm B$.