Exercise 2.5: Three Variants of GF(2 power 4)

Powers of two different extension fields over $\rm GF(2^4)$ - a not quite complete list

Irreducible and primitive polynomials have great importance in the description of error correction methods. For example, in [LN97] one finds the following irreducible polynomials of degree $m = 4$:

$p_1(x) = x^4 + x +1$,

$p_2(x) = x^4 + x^3 + 1$,

$p_3(x) = x^4 + x^3 + x^2 + x + 1$.

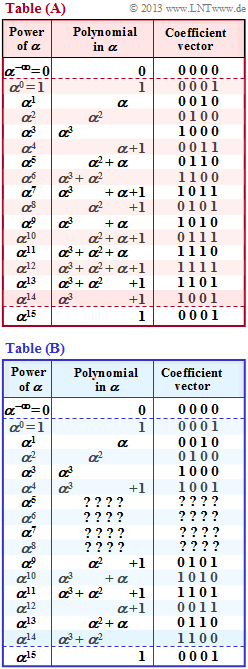
The first two polynomials are also primitive. This can be seen from the power tables given on the right – the lower table $\rm (B)$ however not quite complete.

From both tables we see that all powers $\alpha^i$ for $1 ≤ i ≤ 14$ are unequal $1$ in the polynomial representation. Only for $i = 15$ it follows that

$$\alpha^{15} = \alpha^{0} = 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}{\rm Coefficient\hspace{0.15cm}vector\hspace{0.15cm} 0001}\hspace{0.05cm} .$$

It is not specified whether the tables $\rm (A)$ and $\rm (B)$ result from the polynomial $p_1(x) = x^4 + x + 1$ or from $p_2(x) =x^4 + x^3 + 1$. You are to make these assignments in subtasks (1) and (2).

In the subtask (3) you are also to complete the missing powers $\alpha^5, \ \alpha^6, \ \alpha^7$ and $\alpha^8$ in the table $\rm (B)$.

The subtask (4) refers to the also irreducible polynomial $p_3(x) = x^4 + x^3 + x^2 + x +1$. According to the above criteria, you are to decide whether this polynomial is primitive.

Hints:

The exercise belongs to the chapter "Extension Field".

The literature citation [LN97] refers to the book "Lidl, R.; Niederreiter, H.: Finite Fields. Encyclopedia of Mathematics and its Application. 2nd ed. Cambridge: University Press, 1997."

Questions

Solution

(1) From the upper power table $\rm (A)$ on the data page one recognizes among other things the property

$$\alpha^{4} = \alpha + 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\alpha^{4} + \alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} p(x) = x^4 + x +1 =p_1(x)\hspace{0.05cm}.$$

Thus, the proposed solution 1 is correct.

(2) Following the same procedure, it can be shown that the power table $\rm (B)$ is based on the polynomial $p_2(x) = x^4 + x^3 + 1$ ⇒ Proposed solution 2.

(3) Starting from polynomial $p_2(x) = x^4 + x^3 + 1$ one obtains from the determining equation $p(\alpha) = 0$ the result $\alpha^4 = \alpha^3 + 1$. This further yields:

$$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha \cdot (\alpha^3 + 1) = \alpha^4 + \alpha = \alpha^3 + \alpha +1\hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm vector\hspace{0.15cm} 1011},$$

$$\alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^5 = \alpha \cdot (\alpha^3 +\alpha + 1) = \alpha^4 + \alpha^2 + \alpha= \alpha^3 +\alpha^2 + \alpha + 1\hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm vector\hspace{0.15cm} 1111},$$

$$\alpha^7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^6 = \alpha^4 +\alpha^3 +\alpha^2 +\alpha = \alpha^2 + \alpha + 1\hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm vector\hspace{0.15cm} 0111},$$

$$\alpha^8 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^7 = \alpha \cdot (\alpha^2 + \alpha + 1) = \alpha^3 +\alpha^2 +\alpha \hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm vector\hspace{0.15cm} 1110}.$$

Thus, only the proposed solutions 1 and 4 are correct. The other two statements are interchanged.

The following are the complete power tables for $p_1(x) = x^4 + x + 1$ (left, red background) and for $p_2(x) = x^4 + x^3 + 1$ (right, blue background).

Complete power tables over $\rm GF(2^4)$ for two different polynomials
$($Sorry, we used here the German terms$)$

(4) The polynomials $p_1(x) = x^4 + x + 1$ and $p_2(x) = x^4 + x^3 + 1$ are primitive.

This can be seen from the fact that $\alpha^i \ne 1$ for $0 < i < 14$ in each case.

In contrast, $\alpha^{15} = \alpha^0 = 1$ holds. In both cases, the Galois field can be expressed as follows:

$${\rm GF}(2^4) = \{\hspace{0.1cm}0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} = 1,\hspace{0.05cm}\hspace{0.1cm} \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2},\hspace{0.1cm} ... \hspace{0.1cm} , \hspace{0.1cm}\alpha^{14}\hspace{0.1cm}\}\hspace{0.05cm}. $$

⇒ For the polynomial $p_3(x) = x^4 + x^3 + x^2 + x +1$ we get:

$$\alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^3 + \alpha^2 + \alpha +1\hspace{0.25cm} \Rightarrow\hspace{0.25cm}{\rm vector\hspace{0.15cm} 1111}\hspace{0.05cm},$$

$$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha^4 + \alpha^3 + \alpha^2 + \alpha = $$

$$= (\alpha^3 + \alpha^2 + \alpha +1) + \alpha^3 + \alpha^2 + \alpha = 1 \hspace{0.25cm} \Rightarrow\hspace{0.25cm}{\rm vector\hspace{0.15cm} 0001}\hspace{0.05cm}.$$

So here is already $\alpha^5 = \alpha^0 = 1 $
$\Rightarrow \ p_3(x)$ is not a primitive polynomial ⇒ Proposed solution 2.

For the other powers of this polynomial holds:

$$\alpha^6 = \alpha^{11} = \alpha\hspace{0.05cm},\hspace{0.2cm} \alpha^7 = \alpha^{12} = \alpha^2\hspace{0.05cm},\hspace{0.2cm} \alpha^8 = \alpha^{13} = \alpha^3\hspace{0.05cm},$$

$$\alpha^9 = \alpha^{14} = \alpha^4\hspace{0.05cm},\hspace{0.2cm} \alpha^{10} = \alpha^{15} = \alpha^0 = 1\hspace{0.05cm}.$$

	$\alpha^5 = \alpha^3 + \alpha + 1$ ⇒ Coefficient vector "$1011$",
	$\alpha^6 = \alpha^2 + 1$ ⇒ Coefficient vector "$0111$",
	$\alpha^7 = \alpha^3 + \alpha^2 + \alpha + 1$ ⇒ Coefficient vector "$1111$"
	$\alpha^8 = \alpha^3 + \alpha^2 + \alpha$ ⇒ Coefficient vector "$1110$".

	Yes.
	No.