Exercise 2.5Z: Some Calculations about GF(2 power 3)

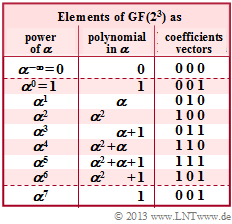
$\rm GF(2^3)$ elements; polynomial $p(x) = x^3 + x + 1$

We consider the extension field with eight elements ⇒ $\rm GF(2^3)$ according to the adjacent table. Since the underlying polynomial

$$p(x) = x^3 + x +1 $$

is both, irreducible and primitive, the Galois field can be stated in the following form:

$${\rm GF}(2^3) = \{\hspace{0.1cm}0\hspace{0.05cm},\hspace{0.1cm} 1,\hspace{0.05cm}\hspace{0.1cm} \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm} \alpha^{3}\hspace{0.05cm},\hspace{0.1cm} \alpha^{4}\hspace{0.05cm},\hspace{0.1cm} \alpha^{5}\hspace{0.05cm},\hspace{0.1cm} \alpha^{6}\hspace{0.1cm}\}\hspace{0.05cm}. $$

The element $\alpha$ results thereby as solution of the equation $p(\alpha) = 0$ in the Galois field $\rm GF(2)$.

This gives the following constraint:

$$\alpha^3 + \alpha +1 = 0\hspace{0.3cm} \Rightarrow\hspace{0.3cm} \alpha^3 = \alpha +1\hspace{0.05cm}.$$

The following calculations apply to the other elements:

$$\alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^3 = \alpha \cdot (\alpha + 1) = \alpha^2 + \alpha \hspace{0.05cm},$$

$$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha \cdot (\alpha^2 +\alpha) = \alpha^3 + \alpha^2 = \alpha^2 + \alpha + 1\hspace{0.05cm},$$

$$\alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^5 = \alpha \cdot (\alpha^2 +\alpha + 1)= \alpha^3 + \alpha^2 + \alpha= \alpha + 1 + \alpha^2 + \alpha = \alpha^2+ 1\hspace{0.05cm}.$$

In this exercise you are to do some algebraic transformations in the Galois field $\rm GF(2^3)$.

Among other things you are asked for the multiplicative inverse of the element $\alpha^4$.

Then it must hold:

$$\alpha^4 \cdot {\rm Inv_M}( \alpha^4) = 1 \hspace{0.05cm}.$$

Hints:

This exercise belongs to the chapter "Extension Field".

This exercise is intended as a supplement to the slightly more difficult "Exercise 2.5".

Questions

Solution

(1) For example, using the table given in the front, you can find:

$$\alpha^7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^6 = \alpha \cdot (\alpha^2 + 1) = \alpha^3 + \alpha = (\alpha + 1) + \alpha = 1 \hspace{0.05cm},$$

$$\alpha^8 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^7 = \alpha \cdot 1 = \alpha\hspace{0.05cm},$$

$$\alpha^{13} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^7 \cdot \alpha^6 = 1 \cdot \alpha^6 = \alpha^2 + 1\hspace{0.05cm}.$$

The table can therefore be continued modulo $7$.

This means: All proposed solutions are correct.

(2) Correct is the proposed solution 2 because of

$\alpha^8 = \alpha$ according to subtask (1),

$\alpha^6 = \alpha^2 + 1$ $($according to the table$)$, and
$-\alpha^2 = \alpha^2$ $($operations in the binary Galois field$)$.

So applies:

$$A = \alpha^8 + \alpha^6 - \alpha^2 + 1 = \alpha + (\alpha^2 + 1) + \alpha^2 + 1 = \alpha \hspace{0.05cm}.$$

(3) With $\alpha^{16} = \alpha^{16-14} = \alpha^2$ and $\alpha^{12} \cdot \alpha^3 = \alpha^{15} = \alpha^{15-14} = \alpha$ we obtain the proposed solution 5:

$$B = \alpha^2 + \alpha= \alpha^4 \hspace{0.05cm}.$$

(4) It holds $\alpha^3 = \alpha + 1$ ⇒ $C = \alpha^3 + \alpha = \alpha + 1 + \alpha = 1$ ⇒ Proposed solution 1.

(5) With $\alpha^4 = \alpha^2 + \alpha$ we obtain $D = \alpha^4 + \alpha = \alpha^2$ ⇒ Proposed solution 3.

(6) Correct is the proposed solution 4:

$$E = A \cdot B \cdot C/D = \alpha \cdot \alpha^4 \cdot 1/\alpha^2 = \alpha^3 \hspace{0.05cm}.$$

(7) According to the table, $\alpha^2 + \alpha = \alpha^4$ holds. Therefore must be valid:

$$\alpha^4 \cdot {\rm Inv_M}( \alpha^4) = 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} {\rm Inv_M}( \alpha^2 + \alpha) = {\rm Inv_M}( \alpha^4) = \alpha^{-4} = \alpha^3 \hspace{0.05cm}.$$

Because of $\alpha^3 = \alpha + 1$ the proposed solutions 2 and 3 are correct.

	$\alpha^7 = 1$,
	$\alpha^8 = \alpha$,
	$\alpha^{13} = \alpha^2 + 1$,
	$\alpha^i = \alpha^{i \ \rm mod \, 7}$.

	$A = 1$,
	$A = \alpha$,
	$A = \alpha^2$,
	$A = \alpha^3$,
	$A = \alpha^4$.

	$B = 1$,
	$B = \alpha$,
	$B = \alpha^2$,
	$B = \alpha^3$,
	$B = \alpha^4$.

	$C = 1$,
	$C = \alpha$,
	$C = \alpha^2$,
	$C = \alpha^3$,
	$C = \alpha^4$.

	$D = 1$,
	$D = \alpha$,
	$D = \alpha^2$,
	$D = \alpha^3$,
	$D = \alpha^4$.

	$E = 1$,
	$E = \alpha$,
	$E = \alpha^2$,
	$E = \alpha^3$,
	$E = \alpha^4$.

	${\rm Inv_M}(\alpha^2 + \alpha) = 1$,
	${\rm Inv_M}(\alpha^2 + \alpha) = \alpha + 1$,
	${\rm Inv_M}(\alpha^2 + \alpha) = \alpha^3$,
	${\rm Inv_M}(\alpha^2 + \alpha) = \alpha^4$.