Exercise 4.3: Iterative Decoding at the BSC

• Return to book

BSC model and possible received values

We consider two codes in this exercise:

• the Single Parity–Code   ⇒   $\text{"SPC (3, 2, 2)"}$:

$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} (0, 1, 1), \hspace{0.1cm} (1, 0, 1), \hspace{0.1cm} (1, 1, 0) \hspace{0.05cm} \big ) \hspace{0.05cm},$$

• the repetition code   ⇒   $\text{"RC (3, 1, 3)"}$:

$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} (1, 1, 1) \hspace{0.05cm} \big ) \hspace{0.05cm}.$$

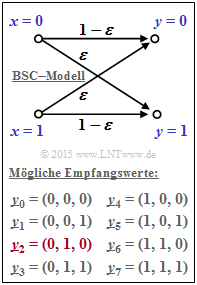
The channel is described at bit level by the  "BSC–model" . According to the graphic, the following applies:

$${\rm Pr}(y_i \ne x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}\varepsilon = 0.269\hspace{0.05cm},$$

$${\rm Pr}(y_i = x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1-\varepsilon = 0.731\hspace{0.05cm}.$$

Here,  $\varepsilon$  denotes the corruption probability of the BSC model.

Except for the last subtask, the following received value is always assumed:

$$\underline{y} = (0, 1, 0) =\underline{y}_2 \hspace{0.05cm}.$$

The here chosen indexing of all possible received vectors can be taken from the graphic.

• The most considered vector  $\underline{y}_2$  is highlighted in red here.
• For the subtask (6) then applies:

$$\underline{y} = (1, 1, 0) =\underline{y}_6 \hspace{0.05cm}.$$

For decoding purposes, the exercise will examine:

• the  "Syndrome Decoding", which follows the concept  hard decision maximum likelihood detection  (HD ML) for the codes under consideration.
  (soft values are not available at the BSC),
• the symbol-wise  "Soft–in Soft–out Decoding"  (SISO) according to this section.

Hints:

• This exercise refers to the chapter  "Soft–in Soft–out Decoder".
• Reference is made in particular to the pages

"Symbol-wise Soft–in Soft–out_Decoding", as well as

Binary Symmetric Channel

• The codeword selected by the decoder is denoted by  $\underline{z}$  in the questions.

Questions

1

Which statements are valid for decoding the  $\text{SPC (3, 2, 2)}$?

	The HD syndrome decoding yields the result  $\underline{z} = (0, \, 1, \, 0)$.
	The HD syndrome decoding returns the result  $\underline{z} = (0, \, 0, \, 0)$.
	The HD syndrome decoding fails here.

2

Which statements are valid for the  $\text{ RC (3, 1, 3)}$?

	The HD syndrome decoding returns the result  $\underline{z} = (0, \, 1, \, 0)$.
	The HD syndrome decoding returns the result  $\underline{z} = (0, \, 0, \, 0)$.
	The HD syndrome decoding fails here.

3

How certain is this decision if we define certainty  $S$  as the quotient of the probabilities for a correct or incorrect decision?
Set the corruption probability of the BSC model to  $\varepsilon = 26.9\%$.

$S \ = \ $

$\hspace{0.75cm} \ln {(S)} \ = \ $

4

What are the intrinsic LLR for the iterative symbol-wise decoding of the  $\text{RC (3, 1)}$ received word  $\underline{y}_2 = (0, \, 1, \, 0)$?

$L_{\rm K}(1) \ = \ $

$L_{\rm K}(2) \ = \ $

$L_{\rm K}(3) \ = \ $

5

Which statements are true for decoding the received word  $\underline{y}_2 = (0, \, 1, \, 0)$ ? Continue to assume the  $\text{RC (3, 1, 3)}$.

	From the first iteration all signs of  $L_{\rm APP}(i)$  are positive.
	Already after the second iteration  ${\rm Pr}(\underline{x}_0\hspace{0.05cm} |\hspace{0.05cm} \underline{y}_2)$  is greater than  $99\%$.
	With each iteration the absolute values  $L_{\rm APP}(i)$  become larger.

6

Which statements are true for decoding the received word  $\underline{y}_6 = (1, 1, 0)$  when  $\underline{x}_0 = (0, 0, 0)$  was sent?

	The iterative decoder decides correctly.
	The iterative decoder decides wrong.
	The "reliability" for "$\underline{y}_6 \Rightarrow \underline{x}_0$" increases with increasing  $I$.

Solution

Solution

(1)  Correct is the proposed solution 3:

• The received word $\underline{y}_2 = (0, 1, 0)$ is not a valid codeword of the single parity–check code SPC (3, 2). Thus, the first statement is false.
• In addition, since the SPC (3, 2) has only the minimum distance $d_{\rm min} = 2$, no error can be corrected.

(2)  Correct is the proposed solution 2:

• The possible codewords at RP (3, 1) are $\underline{x}_0 = (0, 0, 0)$ and $\underline{x}_1 = (1, 1, 1)$.
• The minimum distance of this code is $d_{\rm min} = 3$, so $t = (d_{\rm min} \, - 1)/2 = 1$ error can be corrected.
• In addition to $\underline{y}_0 = (0, 0, 0)$, $\underline{y}_1 = (0, 0, 1), \ \underline{y}_2 = (0, 1, 0)$, and $\underline{y}_4 = (1, 0, 0)$ are also assigned to the decoding result $\underline{x}_0 = (0, 0, 0)$.

(3)  According to the BSC model, the conditional probability is that $\underline{y}_2 = (0, 1, 0)$ is received, given that $\underline{x}_0 = (0, 0, 0)$ was sent:

$${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) = (1-\varepsilon)^2 \cdot \varepsilon\hspace{0.05cm}.$$

• The first term $(1 \, –\varepsilon)^2$ indicates the probability that the first and the third bit were transmitted correctly and $\varepsilon$ considers the corruption probability for the second bit.

• Correspondingly, for the second possible code word $\underline{x}_1 = (1, 1, 1)$:

$${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) = \varepsilon^2 \cdot (1-\varepsilon) \hspace{0.05cm}.$$

• According to Bayes' theorem, the inference probabilities are then:

$${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_0)} {{\rm Pr}(\underline{y} = \underline{y}_2)} \hspace{0.05cm},$$

$${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_1 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_1)} {{\rm Pr}(\underline{y} = \underline{y}_2)}$$

$$\Rightarrow \hspace{0.3cm} S = \frac{{\rm Pr(richtige \hspace{0.15cm}Entscheidung)}} {{\rm Pr(wrong \hspace{0.15cm}decision) }} = \frac{(1-\varepsilon)^2 \cdot \varepsilon}{\varepsilon^2 \cdot (1-\varepsilon)}= \frac{(1-\varepsilon)}{\varepsilon}\hspace{0.05cm}.$$

• With $\varepsilon = 0.269$ we get the following numerical values:

$$S = {0.731}/{0.269}\hspace{0.15cm}\underline {= 2.717}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm ln}\hspace{0.15cm}(S)\hspace{0.15cm} \underline {= 1}\hspace{0.05cm}.$$

(4)  The sign of the channel LLR $L_{\rm K}(i)$ is positive if $y_i = 0$, and negative for $y_i = 1$.

• The absolute value indicates the reliability of $y_i$. In the BSC model, $|L_{\rm K}(i)| = \ln {(1 \, – \varepsilon)/\varepsilon} = 1$ for all $i$. Thus:

Iterative decoding of $(+1, -1, +1)$

$$\underline {L_{\rm K}}(1)\hspace{0.15cm} \underline {= +1}\hspace{0.05cm},\hspace{0.5cm} \underline {L_{\rm K}}(2)\hspace{0.15cm} \underline {= -1}\hspace{0.05cm},\hspace{0.5cm} \underline {L_{\rm K}}(3)\hspace{0.15cm} \underline {= +1}\hspace{0.05cm}.$$

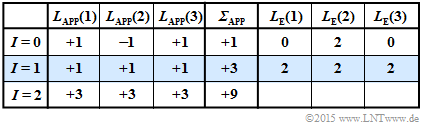
(5)  The adjacent table illustrates the iterative symbol-wise decoding starting from $\underline{y}_2 = (0, \, 1, \, 0)$.
These results can be interpreted as follows:

• The preassignment (iteration $I = 0$) happens according to $\underline{L}_{\rm APP} = \underline{L}_{\rm K}$. A hard decision  ⇒  "$\sign {\underline{L}_{\rm APP}(i)}$" would lead to the decoding result $(0, \, 1, \, 0)$. The reliability of this obviously incorrect result is given as $|{\it \Sigma}| = 1$. This value agrees with the "$\ln (S)$" calculated in subtasks (3).
• After the first iteration $(I = 1)$ all a posteriori LLRs are $L_{\rm APP}(i) = +1$. A hard decision here would yield the (expected) correct result $\underline{x}_{\rm APP} = (0, \, 0, \, 0)$. The probability that this outcome is correct is quantified by $|{\it \Sigma}_{\rm APP}| = 3$:

$${\rm ln}\hspace{0.25cm}\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = 3 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = {\rm e}^3 \approx 20$$

$$\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {20}/{21} {\approx 95.39\%}\hspace{0.05cm}.$$

• The second iteration confirms the decoding result of the first iteration. The reliability is even quantified here with "$9$". This value can be interpreted as follows:

$$\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = {\rm e}^9 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {{\rm e}^9}/{({\rm e}^9+1)} \approx 99.99\% \hspace{0.05cm}.$$

• With each further iteration the reliability value and thus the probability ${\rm Pr}(\underline{x}_0 | \underline{y}_2)$ increases drastically  ⇒  All proposed solutions are correct.

Iterative decoding of $(–1, –1, +1)$

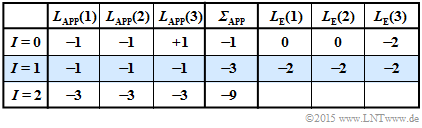
(6)  Correct are the proposed solutions 2 and 3:

• For the received vector $\underline{y}_6 = (1, \, 1, \, 0)$, the second table applies.

• The decoder now decides for the sequence $\underline{x}_1 = (1, \, 1, \, 1)$.
• The case "$\underline{y}_3 = (1, \, 1, \, 0)$ received under the condition $\underline{x}_1 = (1, \, 1, \, 1)$ sent" would correspond exactly to the constellation "$\underline{y}_2 = (1, \, 0, \, 1)$ received and $\underline{x}_0 = (0, \, 0, \, 0)$ sent" considered in the last subtask.
• But since $\underline{x}_0 = (0, \, 0, \, 0)$ was sent, there are now two bit errors with the following consequence:

• The iterative decoder decides incorrectly.
• With each further iteration the wrong decision is declared as more reliable.