The Basics of Product Codes

1. Channel Coding
2. Iterative Decoding Methods
3. The Basics of Product Codes

• Previous page
• Next page

• Previous page
• Next page

Basic structure of a product code

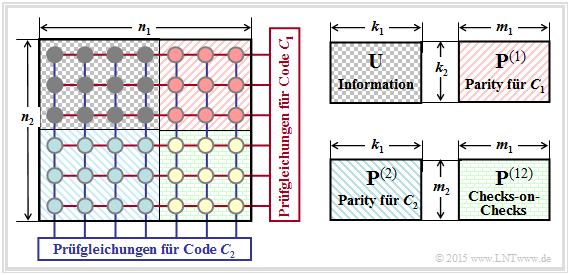
The graphic shows the principle structure of product codes, which were already introduced in 1954 by  "Peter Elias" . The  two-dimensional product code  $\mathcal{C} = \mathcal{C}_1 × \mathcal{C}_2$  shown here is based on the two linear and binary block codes with parameters  $(n_1, \ k_1)$  and  $(n_2, \ k_2)$ respectively. The code word length is  $n = n_1 \cdot n_2$.

Basic structure of a product code

These  $n$  code bits can be grouped as follows:

• The  $k = k_1 \cdot k_2$  information bits are arranged in the  $k_2 × k_1$ matrix  $\mathbf{U}$ . The code rate is equal to the product of the code rates of the two base codes:

$$R = k/n = (k_1/n_1) \cdot (k_2/n_2) = R_1 \cdot R_2.$$

• The upper right matrix  $\mathbf{P}^{(1)}$  with dimension  $k_2 × m_1$  contains the parity bits with respect to the code  $\mathcal{C}_1$. In each of the  $k_2$  rows, check bits are added to the  $k_1$ information bits  $m_1 = n_1 - k_1$  as described in an earlier chapter using the example of  "Hamming codes" .
  

• The lower left matrix  $\mathbf{P}^{(2)}$  of dimension  $m_2 × k_1$  contains the check bits for the second component code  $\mathcal{C}_2$. Here the encoding (and also the decoding) is done line by line:   In each of the  $k_1$  columns the  $k_2$  information bits are still supplemented by  $m_2 = n_2 -k_2$  check bits.
  

• The  $m_2 × m_1$–matrix  $\mathbf{P}^{(12)}$  on the bottom right is called  checks–on–checks. Here the two previously generated parity matrices  $\mathbf{P}^{(1)}$  and  $\mathbf{P}^{(2)}$  are linked according to the parity-check equations.
  
  

$\text{Conclusion:}$  All product codes according to the above graphic have the following properties:

• For linear component codes  $\mathcal{C}_1$  and  $\mathcal{C}_2$  the product code  $\mathcal{C} = \mathcal{C}_1 × \mathcal{C}_2$  is also linear.
  

• Each row of  $\mathcal{C}$  returns a code word of  $\mathcal{C}_1$  and each column returns a code word of  $\mathcal{C}_2$.
  

• The sum of two rows again gives a code word of  $\mathcal{C}_1$ due to linearity.
  

• Also, the sum of two columns gives a valid code word of  $\mathcal{C}_2$.
  

• Each product code also includes the zero word  $\underline{0}$  (a vector of  $n$  zeros).
  

• The minimum distance of  $C$  is  $d_{\rm min} = d_1 \cdot d_2$, where  $d_i$  indicates the minimum distance of  $\mathcal{C}_i$ 

Iterative syndrome decoding of product codes

We now consider the case where a product code with matrix  $\mathbf{X}$  is transmitted over a binary channel. Let the receive matrix  $\mathbf{Y} = \mathbf{X} + \mathbf{E}$, where  $\mathbf{E}$  denotes the error matrix. Let all elements of the matrices  $\mathbf{X}, \ \mathbf{E}$  and  $\mathbf{Y}$ be binary, that is  $0$  or  $1$.

For the decoding of the two component codes the syndrome decoding according to the chapter  "Decoding linear block codes"  is suitable.

In the two-dimensional case this means:

• One first decodes the  $n_2$  rows of the receive matrix  $\mathbf{Y}$, based on the parity-check matrix  $\mathbf{H}_1$  of the component code  $\mathcal{C}_1$. Syndrome decoding is one way to do this.
  

• For this one forms in each case the so-called syndrome  $\underline{s} = \underline{y} \cdot \mathbf{H}_1^{\rm T}$, where the vector  $\underline{y}$  of length  $n_1$  indicates the current row of  $\mathbf{Y}$  and "T" stands for "transposed". Corresponding to the calculated  $\underline{s}_{\mu}$  $($with  $0 ≤ \mu < 2^{n_1 -k_1})$  one finds in a prepared syndrome table the corresponding probable error pattern  $\underline{e} = \underline{e}_{\mu}$.
  

• If there are only a few errors within the row, then  $\underline{y} + \underline{e}$  matches the sent row vector  $\underline{x}$ . However, if too many errors have occurred, the following incorrect corrections will occur.
  

• Then one "syndromedecodes" the  $n_1$  columns of the (corrected) received matrix  $\mathbf{Y}\hspace{0.03cm}'$, this time based on the (transposed) parity-check matrix  $\mathbf{H}_2^{\rm T}$  of the component code  $\mathcal{C}_2$. For this, one forms the syndrome  $\underline{s} = \underline{y}\hspace{0.03cm}' \cdot \mathbf{H}_2^{\rm T}$, where the vector  $\underline{y}\hspace{0.03cm}'$  of length  $n_2$  denotes the considered column of  $\mathbf{Y}\hspace{0.03cm}'$  .
  

• From a second syndrome table $($valid for the code  $\mathcal{C}_2)$  we find for the computed  $\underline{s}_{\mu}$  $($with  $0 ≤ \mu < 2^{n_2 -k_2})$  the probable error pattern $\underline{e} = \underline{e}_{\mu}$ of the edited column. After correcting all columns, the matrix  $\mathbf{Y}$  is present. Now one can do another row and then a column decoding   ⇒   second iteration, and so on, and so forth.
  
  

$\text{Example 1:}$  To illustrate the decoding algorithm, we again consider the  $(42, 12)$ product code, based on

• the Hamming code  $\text{HC (7, 4, 3)}$   ⇒   code  $\mathcal{C}_1$,
  

• the shortened Hamming code  $\text{HC (6, 3, 3)}$   ⇒   code  $\mathcal{C}_2$.
  

The left graph shows the receive matrix  $\mathbf{Y}$. For display reasons, the code matrix  $\mathbf{X}$  was chosen to be a  $6 × 7$ zero matrix, so that the nine ones in  $\mathbf{Y}$  represent transmission errors at the same time.

Syndrome decoding of the  $(42, 12)$ product code

The  row by row syndrome decoding  is done via the syndrome  $\underline{s} = \underline{y} \cdot \mathbf{H}_1^{\rm T}$  with

$$\boldsymbol{\rm H}_1^{\rm T} = \begin{pmatrix} 1 &0 &1 \\ 1 &1 &0 \\ 0 &1 &1 \\ 1 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$

In particular:

Syndrome table for code $\mathcal{C}_1$

• Row 1  ⇒  Single error correction is successful (also in rows 3,  4 and 6):

$$\underline{s} = \left ( 0, \hspace{0.02cm} 0, \hspace{0.02cm}1, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H} }_1^{\rm T} \hspace{-0.05cm}= \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}1 \right ) = \underline{s}_3$$

$$\Rightarrow \hspace{0.3cm} \underline{y} + \underline{e}_3 = \left ( 0, \hspace{0.02cm} 0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0 \right ) \hspace{0.05cm}.$$

• Row 2  (contains two errors)   ⇒   Error correction concerning bit 5:

$$\underline{s} = \left ( 1, \hspace{0.02cm} 0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}1 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H} }_1^{\rm T} \hspace{-0.05cm}= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right ) = \underline{s}_4$$

$$\Rightarrow \hspace{0.3cm} \underline{y} + \underline{e}_4 = \left ( 1, \hspace{0.02cm} 0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}0, \hspace{0.02cm}1 \right ) \hspace{0.05cm}.$$

• Row 5  (also contains two errors)  ⇒  Error correction concerning bit 3:

$$\underline{s} = \left ( 0, \hspace{0.02cm} 0, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}1, \hspace{0.02cm}0, \hspace{0.02cm}0 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H} }_1^{\rm T} \hspace{-0.05cm}= \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}1 \right ) = \underline{s}_3$$

$$\Rightarrow \hspace{0.3cm} \underline{y} + \underline{e}_3 = \left ( 0, \hspace{0.02cm} 0, \hspace{0.02cm}1, \hspace{0.02cm}1, \hspace{0.02cm}1, \hspace{0.02cm}0, \hspace{0.02cm}0 \right ) \hspace{0.05cm}.$$

The column by column syndrome decoding removes all single errors in columns  1,  2,  3,  4  and  7.

Syndrome table for the code $\mathcal{C}_2$

• Column 5  (contains two errors)   ⇒   Error correction concerning bit 4:

$$\underline{s} = \left ( 0, \hspace{0.02cm} 1, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}0 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H} }_2^{\rm T} \hspace{-0.05cm}= \left ( 0, \hspace{0.02cm} 1, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}0 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm} \begin{pmatrix} 1 &1 &0 \\ 1 &0 &1 \\ 0 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix} = \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right ) = \underline{s}_4$$

$$\Rightarrow \hspace{0.3cm} \underline{y} + \underline{e}_4 = \left ( 0, \hspace{0.02cm} 1, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}1, \hspace{0.02cm}0 \right ) \hspace{0.05cm}.$$

The remaining three errors are corrected by decoding the  second iteration loop  line by line.

Whether all errors of a block are correctable depends on the error pattern. Here we refer to the  "Exercise 4.7"

Performance of product codes

The 1954 introduced  product codes  were the first codes, which were based on recursive construction rules and thus in principle suitable for iterative decoding. The inventor Peter Elias did not comment on this, but in the last twenty years this aspect and the simultaneous availability of fast processors have contributed to the fact that in the meantime product codes are also used in real communication systems, e.g.

• in error protection of storage media, and
• in very high data rate fiber optic systems.
  

Usually one uses very long product codes  $($large  $n = n_1 \cdot n_2)$  with the following consequence:

• For effort reasons, the  "Maximum Likelihood Decoding at block level"  not applicable for component codes  $\mathcal{C}_1$  and  $\mathcal{C}_2$  nor the  "syndrome decoding", which is after all a realization form of ML decoding.

• Applicable, on the other hand, even with large  $n$  is the  "iterative symbol-wise MAP decoding". The exchange of extrinsic and apriori–information happens here between the two component codes. More details on this can be found in  [Liv15].
  

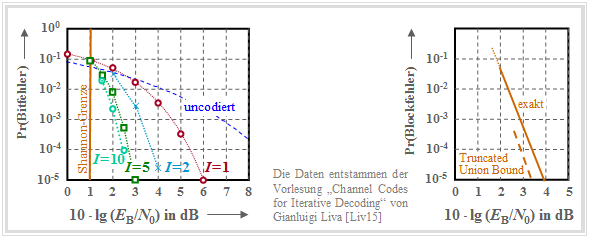
The graph shows for a  $(1024, 676)$ product code, based on the  extended Hamming code  ${\rm eHC} \ (32, 26)$  as component codes,

• on the left, the AWGN bit error probability as a function of iterations  $(I)$
• right the error probability of the blocks (or code words).

Bit and block error probability of a  $(1024, 676)$ product code at AWGN

Here are some additional remarks:

• The code rate is  $R = R_1 \cdot R_2 = 0.66$, giving the Shannon bound to  $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx 1 \ \rm dB$  results.
  

• In the left graph you can see the influence of the iterations. At the transition from  $I = 1$  to  $I=2$  one gains approx.  $2 \ \rm dB$ $($at the bit error rate  $10^{-5})$  and with  $I = 10$  another $\rm dB$. Further iterations are not worthwhile.
  

• All bounds mentioned in the chapter  "Bounds for Block Error Probability"  can be applied here as well, so also the one shown dashed in the right graph  truncated union bound:

$${\rm Pr(Truncated\hspace{0.15cm}Union\hspace{0.15cm} Bound)}= W_{d_{\rm min}} \cdot {\rm Q} \left ( \sqrt{d_{\rm min} \cdot {2R \cdot E_{\rm B}}/{N_0}} \right ) \hspace{0.05cm}.$$

• The minimum distance is  $d_{\rm min} = d_1 \cdot d_2 = 4 \cdot 4 = 16$. With the weight function of the  ${\rm eHC} \ (32, 26)$,

$$W_{\rm eHC(32,\hspace{0.08cm}26)}(X) = 1 + 1240 \cdot X^{4} + 27776 \cdot X^{6}+ 330460 \cdot X^{8} + ...\hspace{0.05cm} + X^{32},$$

is obtained for the product code  $W_{d, \cdot min} = 1240^2 = 15\hspace{0.05cm}376\hspace{0.05cm}000$. This gives the error probability shown in the graph on the right.

Exercises for the chapter

"Exercise 4.6: Product Code Generation"

"Exercise 4.6Z: Basics of Product Codes"

"Exercise 4.7: Product Code Decoding"

"Exercise 4.7Z: Principle of Syndrome Decoding"