Exercise 1.5: HDB3 Coding

Signals with HDB3 coding

The ISDN primary rate interface $\rm (PRI)$ is based on the $\rm PCM\ system \ 30/32$ and offers

$30$ full-duplex basic channels,

plus a signaling channel

and a synchronization channel.

Each of these channels, which are transmitted in time division multiplex, has a data rate of $64 \ \rm kbit/s$. A frame consists of one byte $\rm (8$ bits$)$ of all $32$ channels. The duration of such a frame $($German: "Rahmen"$)$ is denoted by $T_{\rm R}$, while $T_{\rm B}$ indicates the bit duration.

On both the $\rm S_{\rm 2M}$ and $\rm U_{\rm K2}$ interfaces of the ISDN system under consideration, the HDB3 code is used, which is derived from the AMI code. This is a pseudo-ternary code $($symbol set size $M = 3$, symbol duration $T = T_{\rm B})$, that differs from the AMI code in that long zero sequences are avoided by deliberately violating the AMI coding rule. The following applies:

If four consecutive "0" symbols occur in the AMI-encoded signal $a(t)$, these are replaced by four other ternary symbols:

If an even number of "+1" occurred before this four-symbol block the signal $a(t)$ and the last pulse is positive, "0 0 0 0" is replaced by "– 0 0 –". If the last pulse is negative, "0 0 0 0" is replaced by "+ 0 0 +".

On the other hand, if there is an odd number of "ones" before this "0 0 0 0" block, "0 0 0 +" $($if last pulse positive$)$ or "0 0 0 –" $($if last pulse negative$)$ are selected.

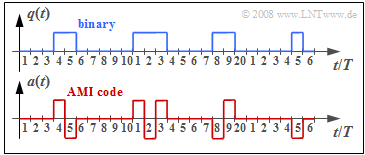
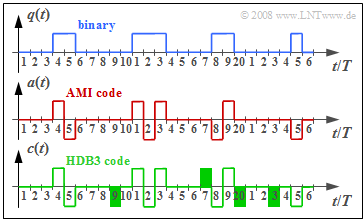
The graph above shows the binary signal $q(t)$ and the signal $a(t)$ after AMI coding. The HDB3 signal is denoted by $c(t)$.

Notes:

The exercise belongs to the chapter "ISDN Primary Multiplex Connection" .
Information about the pseudo-ternary codes can be found in the section "Symbolwise Coding with Pseudo-Ternary Codes" of "Digital Signal Transmission".

Questions

$R_{\rm B} \ = \ $

$\ \rm Mbit/s$

$T_{\rm B} \ = \ $

$\ \rm µ s$

$T_{\rm R} \ = \ $

$\ \rm µ s$

$c_{6} \ = \ $

$c_{7} \ = \ $

$c_{8} \ = \ $

$c_{9} \ = \ $

$c_{10} \ = \ $

$c_{14} \ = \ $

$c_{15} \ = \ $

$c_{16} \ = \ $

$c_{17} \ = \ $

$c_{20} \ = \ $

$c_{21} \ = \ $

$c_{22} \ = \ $

$c_{23} \ = \ $

$c_{24} \ = \ $

Solution

(1) The total data rate of the $32$ channels at $64 \ \rm kbit/s$ each results in

$$R_{\rm B} \underline{ = 2.048 \ \rm Mbit/s}.$$

(2) The bit duration is $T_{\rm B} = 1/R_{\rm B} \underline{ = 0.488 \ \rm µ s}$.

One byte (8 bits) of each channel is transmitted per frame. It follows that:

$$T_{\rm R} = 32 \cdot 8 \cdot T_{\rm B} \hspace{0.15cm}\underline{= 125 \,{\rm µ s}}\hspace{0.05cm}.$$

(3) By time $t = 6T$, a "+1" has occurred exactly once in the AMI-encoded signal $a(t)$.

Relationship between AMI code and HDB3 code

Because of $a_{5} = –1$, in the HDB3 code "0 0 0 0" is replaced by (see diagram)

$$\underline{c_{6} = 0, \hspace{0.2cm}c_{7} = 0, \hspace{0.2cm}c_{8} = 0, \hspace{0.2cm}c_{9} = -1} \hspace{0.05cm}.$$

In contrast, $\underline{c_{10} = a_{10} = 0}$ is not changed bythe HDB3 coding.

(4) Up to and including $a_{13}$, there are three times a "+1" ⇒ odd number. Because of $a_{12} = +1$, this zero block is replaced as follows:

$$ \underline{c_{14} = 0, \hspace{0.2cm}c_{15} = 0, \hspace{0.2cm}c_{16} = 0, \hspace{0.2cm}c_{17} = +1} \hspace{0.05cm}.$$

(5) In the AMI-encoded signal, "+1" occurs exactly four times up to and including $a_{19}$ ⇒ even number.

Because of $a_{19} = +1$, the substitution according to rule 2 in the information section is:

$$\underline{c_{20} = -1, \hspace{0.2cm}c_{21} = 0, \hspace{0.2cm}c_{22} = 0, \hspace{0.2cm}c_{23} = -1} \hspace{0.05cm}.$$

The zero symbol $a_{24}$ remains unchanged: $\underline{c_{24} = 0}$.