Exercise 3.09: Basics of the Viterbi Algorithm

• Return to book

Trellis to be analyzed

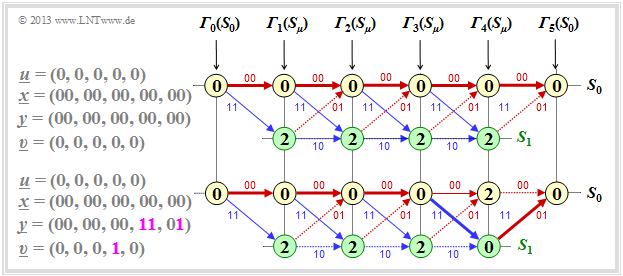
The graph shows a trellis diagram and simultaneously defines the accumulated error values  $($"metrics"$)$   ${\it \Gamma}_i(S_0)$  and  ${\it \Gamma}_i(S_1)$  at times  $i = 0$  to  $i = 5$.

From this trellis can be read,  for example:

• the code rate  $R$,

• the memory  $m$,

• the free distance  $d_{\rm F}$,

• the information sequence length  $L$,

• the sequence length  $L\hspace{0.05cm}'$  including the termination.

In the exercise it is further necessary to clarify:

• the meaning of the final error value  ${\it \Gamma}_5(S_0)$,

• effects of one and two transmission errors,  respectively.

Hint:  This exercise belongs to the chapter  "Decoding of Convolutional Codes".

Questions

1

Which of the following statements are confirmed by the trellis?

	It is a rate-1/2 convolutional code.
	The memory of the code is  $m = 2$.
	The convolutional code is terminated.
	The length of the information sequence is  $L = 5$.

2

Specify the free distance  $d_{\rm F}$  of the convolutional code.

$d_{\rm F} \ = \ $

3

What statements does the final value  ${\it \Gamma}_5(S_0) = 0$  of the metric allow?

	No transmission error has occurred.
	The decoding result   $\underline{v}$   is certainly correct  $($equal  $\underline{u})$.
	The decoding result minimizes the probability   ${\rm Pr}(\underline{v} ≠ \underline{u})$.

4

Which statements are true  in the case of a single  transmission error?

	The final metric is  ${\it \Gamma}_5(S_0) = 1$.
	The decoding result  $\underline{v}$  is certainly correct  $($equal  $\underline{u})$.
	The decoding result minimizes the probability   ${\rm Pr}(\underline{v} ≠ \underline{u})$.

5

Which statements are true  in the case of two  transmission errors?

	The final metric is  ${\it \Gamma}_5(S_0) = 2$.
	The decoding result  $\underline{v}$  is certainly correct  $($equal  $\underline{u})$.
	The decoding result  $\underline{v}$  is certainly false  $($unequal  $\underline{u})$.

Solution

Solution

(1)  Correct are the  solutions 1 and 3:

• There are   $2^{k \cdot m} = 2$   states here.  It follows that  $k = 1$  and  $m = 1$.

• Per coding step,  $n = 2$  code bits are output   ⇒   $R = 1/2$.

• The information sequence length is  $L = 4$.

• Only by one  $($since  $m = 1)$  additional termination bit one arrives at the total length  $L' = 5$.

(2)  The free distance  $d_{\rm F}$  is defined as the number of code bits in which two sequences  $\underline{x}$  and  $\underline{x'}$  differ. 

• We choose the zero sequence as the reference sequence:

$$\underline{x}\hspace{0.03cm}' = \underline{0} = \big (00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.05cm},$$

expressed with the sequence of states:   $S_0 → S_0 → S_0 → S_0 → \ \text{...} \ $

• One of the sequences  $\underline{x} ≠ \underline{0}$,  which differs from   $\underline{0}$   only in the minimum number of code bits,  follows the path  $S_0 → S_1 → S_0 → S_0 → \text{...} \ $:

$$\underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} d_{\rm F}\hspace{0.1cm}\underline{ = 3} \hspace{0.05cm}.$$

Trellis without error  (above)  and with three transmission errors  (below)

Trellis with two transmission errors

(3)  Only  proposition 3  is correct here,  because the event  "No transmission error"  is much more likely than three errors at exactly specified positions.  Consider the graph:

• If the zero sequence is sent and this is also received,  the Viterbi decoding can be illustrated by the upper trellis.

• The final value of the metric is  ${\it \Gamma}_5(S_0) = 0$,  and the Viterbi decoder decides correctly with certainty:   $\underline{z} = \underline{x}  ⇒  \underline{v} = \underline{u}$.

• For the lower trellis,  we also assume  $\underline{u} = (0, \, 0, \, 0, \, 0 \, 0)   ⇒   \underline{x} = (00, \, 00, \, 00, \, 00, \, 00)$.

• However,  $\underline{y} = (00, \, 00, \, 00, \, 11, \, 01)$  is received now. 

• Nevertheless,  ${\it \Gamma}_5(S_0) = 0$  holds.  The example proves that the first two statements are false.

(4)  Correct are all answers:  If it is known for sure that only one transmission error occurred,  for a convolutional code with free distance  $d_{\rm F} = 3$  the Viterbi algorithm works perfectly,  no matter at which position the error occurred.

(5)  None of the proposed solutions is correct, as can be seen from the examples below.