Allgemeine Beschreibung
Zufallsgrößen mit Gaußscher Wahrscheinlichkeitsdichtefunktion – die Namensgebung geht dabei auf den bedeutenden Mathematiker, Physiker und Astronomen Carl Friedrich Gauß zurück – sind wirklichkeitsnahe Modelle für viele physikalische Größen und haben auch für die Nachrichtentechnik eine große Bedeutung. Dies hat mehrere Gründe:
- Nach dem zentralen Grenzwertsatz besitzt jede Linearkombination statistischer Größen
$$x=\sum\limits_{i=\rm 1}^{\it I}x_i ,$$
- im Grenzfall $(I → ∞)$ eine Gaußsche WDF, so lange die einzelnen Komponenten keine statistischen Bindungen besitzen. Dies gilt (nahezu) für alle Dichtefunktionen der einzelnen Summanden $x_i$.
- Viele Rauschprozesse erfüllen genau diese Voraussetzung, das heißt, sie setzen sich additiv aus einer sehr großen Anzahl voneinander unabhängiger Einzelbeiträge zusammen, so dass ihre Musterfunktionen (Rauschsignale) eine Gaußsche Amplitudenverteilung aufweisen.
- Legt man ein gaußverteiltes Signal zur spektralen Formung an ein lineares Filter, so ist das Ausgangssignal ebenfalls gaußverteilt. Es ändern sich nur die Verteilungsparameter wie Mittelwert und Streuung sowie die inneren statistischen Bindungen der Abtastwerte.
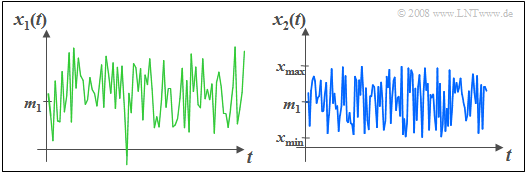
Das Bild zeigt links ein Gaußsches Zufallssignal $x_1(t)$ und rechts im Vergleich dazu ein gleichverteiltes Signal $x_2(t)$ mit gleichem Mittelwert $m_1$ und gleicher Streuung $σ$.
Man erkennt, dass bei der Gaußverteilung im Gegensatz zur Gleichverteilung beliebig große und beliebig kleine Amplitudenwerte auftreten können, auch wenn diese sehr unwahrscheinlich sind im Vergleich zum mittleren Amplitudenbereich.
Wahrscheinlichkeitsdichte- und Verteilungsfunktion
Die Wahrscheinlichkeitsdichtefunktion einer gaußverteilten Zufallsgröße lautet allgemein: $$f_x(x) = \frac{1}{\sqrt{2\pi}\cdot\sigma}\cdot {\rm exp}\left (-\frac{(x-m_1)^2 }{2\sigma^2} \right ).$$ Die Parameter einer Gaußschen WDF sind
- der Mittelwert bzw. der Gleichanteil $m_1$,
- die Streuung bzw. der Effektivwert $σ$.
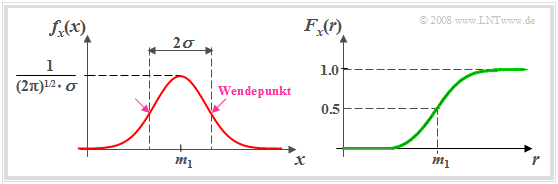
Aus der linken Darstellung geht hervor, dass die Streuung $σ$ als der Abstand von Maximalwert und Wendepunkt aus der glockenförmigen WDF $f_{\rm x}(x)$ auch grafisch ermittelt werden kann. Ist $m_1 =$ 0 und $σ =$ 1, so spricht man oft auch von der Normalverteilung.
Rechts ist die Verteilungsfunktion $F_{\rm x}(r)$ einer gaußverteilten Zufallsgröße dargestellt. Die VTF ist punktsymmetrisch um den Mittelwert $m_1$. Durch Integration über die Gaußsche WDF erhält man: $$F_x(r)= \phi(\frac{\it r-m_{\rm 1}}{\sigma})\hspace{0.5cm}\rm mit\hspace{0.5cm}\rm \phi (\it x) = \frac{\rm 1}{\sqrt{\rm 2\it \pi}}\int_{-\rm\infty}^{\it x} \rm e^{\it -u^{\rm 2}/\rm 2}\,\, d \it u.$$
Man bezeichnet $ϕ(x)$ als das Gaußsche Fehlerintegral. Dessen Funktionsverlauf ist analytisch nicht berechenbar und muss deshalb aus Tabellen entnommen werden. $ϕ(x)$ lässt sich durch eine Taylorreihe annähern oder aus der in Programmbibliotheken oft vorhandenen Funktion „erf( $x$)” berechnen.
Weitere Informationen zu den gaußverteilten Zufallsgrößen liefert das folgende Lernvideo: Der AWGN–Kanal – Teil 2