PDF, CDF and Moments of Special Distributions

Open Applet in new Tab   Deutsche Version Öffnen

Applet Description

Das Applet stellt die Beschreibungsformen zweier wertkoninuierlicher Zufallsgrößen  $X$  und  $Y\hspace{-0.1cm}$  vergleichend gegenüber, wobei für die rote Zufallsgröße  $X$  und die blaue Zufallsgröße  $Y$  jeweils folgende Grundformen zur Auswahl stehen:

• Gaußverteilung, Gleichverteilung, Dreieckverteilung, Exponentialverteilung, Laplaceverteilung, Rayleighverteilung, Riceverteilung, Weibullverteilung, Wigner–Halbkreisverteilung, Wigner–Parabelverteilung, Cauchyverteilung.

Die folgenden Angaben beziehen sich auf die Zufallsgrößen  $X$. Graphisch dargestellt werden

• die Wahrscheinlichkeitsdichtefunktion  $f_{X}(x)$  (oben) und
• die Verteilungsfunktion  $F_{X}(x)$  (unten).

Zusätzlich werden noch einige integrale Kenngrößen ausgegeben, nämlich

• der lineare Mittelwert  $m_X = {\rm E}\big[X \big]$,
• der quadratische Mittelwert  $P_X ={\rm E}\big[X^2 \big]$,
• die Varianz  $\sigma_X^2 = P_X - m_X^2$,
• die Standardabweichung (oder Streuung)  $\sigma_X$,
• die Charliersche Schiefe  $S_X$,
• die Kurtosis  $K_X$.

Definition and Properties of the Presented Descriptive Variables

In diesem Applet betrachten wir ausschließlich (wert–)kontinuierliche Zufallsgrößen, also solche, deren mögliche Zahlenwerte nicht abzählbar sind.

• Der Wertebereich dieser Zufallsgrößen ist somit im allgemeinen der der reellen Zahlen  $(-\infty \le X \le +\infty)$.
• Es ist aber möglich, dass der Wertebereich auf ein Intervall begrenzt ist:  $x_{\rm min} \le X \le +x_{\rm max}$.

Probability density function (PDF)

For a continuous random variable  $X$  the probabilities that  $X$  takes on quite specific values  $x$  are zero:  ${\rm Pr}(X= x) \equiv 0$.  Therefore, to describe a continuous random variable, we must always refer to the  probability density function  – in short  $\rm WDF$. 

$\text{Definition:}$  The value of the  »probability density function«  $f_{X}(x)$  at location  $x$  is equal to the probability that the instantaneous value of the random variable  $x$  lies in an  (infinitesimally small)  interval of width  $Δx$  around  $x_\mu$,  divided by  $Δx$:

$$f_X(x) = \lim_{ {\rm \Delta} x \hspace{0.05cm}\to \hspace{0.05cm} 0} \frac{ {\rm Pr} \big [x - {\rm \Delta} x/2 \le X \le x +{\rm \Delta} x/2 \big ] }{ {\rm \Delta} x}.$$

This extremely important descriptive variable has the following properties:

• For the probability that the random variable  $X$  lies in the range between  $x_{\rm u}$  and  $x_{\rm o} > x_{\rm u}$: 

$${\rm Pr}(x_{\rm u} \le X \le x_{\rm o}) = \int_{x_{\rm u}}^{x_{\rm o}} f_{X}(x) \ {\rm d}x.$$

• As an important normalization property,  this yields for the area under the PDF with the boundary transitions  $x_{\rm u} → \hspace{0.1cm} – \hspace{0.05cm} ∞$  and  $x_{\rm o} → +∞$:

$$\int_{-\infty}^{+\infty} f_{X}(x) \ {\rm d}x = 1.$$

Cumulative distribution function (VTF)

The  cumulative distribution function  – in short  $\rm CDF$  – provides the same information about the random variable  $X$  as the probability density function.

$\text{Definition:}$  The  »cumulative distribution function«  $F_{X}(x)$  corresponds to the probability that the random variable  $X$  is less than or equal to a real number  $x$: 

$$F_{X}(x) = {\rm Pr}( X \le x).$$

The CDF has the following characteristics:

• The CDF is computable from the probability density function  $f_{X}(x)$  by integration.  It holds:

$$F_{X}(x) = \int_{-\infty}^{x}f_X(\xi)\,{\rm d}\xi.$$

• Since the PDF is never negative,  $F_{X}(x)$  increases at least weakly monotonically,  and always lies between the following limits:

$$F_{X}(x → \hspace{0.1cm} – \hspace{0.05cm} ∞) = 0, \hspace{0.5cm}F_{X}(x → +∞) = 1.$$

• Inversely,  the probability density function can be determined from the CDF by differentiation:

$$f_{X}(x)=\frac{{\rm d} F_{X}(\xi)}{{\rm d}\xi}\Bigg |_{\hspace{0.1cm}x=\xi}.$$

• For the probability that the random variable  $X$  is in the range between  $x_{\rm u}$  and  $x_{\rm o} > x_{\rm u}$  holds:

$${\rm Pr}(x_{\rm u} \le X \le x_{\rm o}) = F_{X}(x_{\rm o}) - F_{X}(x_{\rm u}).$$

Erwartungswerte und Momente

Die Wahrscheinlichkeitsdichtefunktion bietet ebenso wie die Verteilungsfunktion sehr weitreichende Informationen über die betrachtete Zufallsgröße. Weniger, aber dafür kompaktere Informationen in Form einzelner Zahlenwerte liefern die so genannten  Erwartungswerte  und  Momente.

$\text{Definition:}$  Der  Erwartungswert  bezüglich einer beliebigen Gewichtungsfunktion  $g(x)$  kann mit der WDF  $f_{\rm X}(x)$  in folgender Weise berechnet werden:

$${\rm E}\big[g (X ) \big] = \int_{-\infty}^{+\infty} g(x)\cdot f_{X}(x) \,{\rm d}x.$$

Setzt man in diese Gleichung für  $g(x) = x^k$  ein, so erhält man das  Moment $k$-ter Ordnung:

$$m_k = {\rm E}\big[X^k \big] = \int_{-\infty}^{+\infty} x^k\cdot f_{X} (x ) \, {\rm d}x.$$

Aus dieser Gleichung erhält man

• mit  $k = 1$  für den  linearen Mittelwert:

$$m_1 = {\rm E}\big[X \big] = \int_{-\infty}^{ \rm +\infty} x\cdot f_{X} (x ) \,{\rm d}x,$$

• mit  $k = 2$  für den  quadratischen Mittelwert:

$$m_2 = {\rm E}\big[X^{\rm 2} \big] = \int_{-\infty}^{ \rm +\infty} x^{ 2}\cdot f_{ X} (x) \,{\rm d}x.$$

In Zusammenhang mit Signalen sind auch folgende Bezeichnungen üblich:

• $m_1$  gibt den  Gleichanteil  an;    bezüglich der Zufallsgröße  $X$  schreiben wir im Folgenden auch  $m_X$.
• $m_2$  entspricht der  (auf den Einheitswiderstand  $1 \ Ω$  bezogenen) Signalleistung  $P_X$.

Bezeichnet  $X$  beispielsweise eine Spannung, so hat nach diesen Gleichungen  $m_X$  die Einheit  ${\rm V}$  und die Leistung  $P_X$  die Einheit  ${\rm V}^2.$ Will man die Leistung in „Watt”  $\rm (W)$ angeben, so muss  $P_X$  noch durch den Widerstandswert  $R$  dividiert werden.

Zentralmomente

Besondere Bedeutung haben in der Statistik allgemein die so genannten  Zentralmomente, von denen viele Kenngrößen abgeleitet werden,

$\text{Definition:}$  Die  Zentralmomente  sind im Gegensatz zu den herkömmlichen Momenten jeweils auf den Mittelwert  $m_1$  bezogen. Für diese gilt mit  $k = 1, \ 2,$ ...:

$$\mu_k = {\rm E}\big[(X-m_{\rm 1})^k\big] = \int_{-\infty}^{+\infty} (x-m_{\rm 1})^k\cdot f_x(x) \,\rm d \it x.$$

• Bei mittelwertfreien Zufallsgrößen stimmen die zentrierten Momente  $\mu_k$  mit den nichtzentrierten Momente  $m_k$  überein.

• Das Zentralmoment erster Ordnung ist definitionsgemäß gleich  $\mu_1 = 0$.

• Die nichtzentrierten Momente  $m_k$  und die Zentralmomente  $\mu_k$  können direkt ineinander umgerechnet werden.  Mit  $m_0 = 1$  und  $\mu_0 = 1$  gilt dabei:

$$\mu_k = \sum\limits_{\kappa= 0}^{k} \left( \begin{array}{*{2}{c}} k \\ \kappa \\ \end{array} \right)\cdot m_\kappa \cdot (-m_1)^{k-\kappa},$$

$$m_k = \sum\limits_{\kappa= 0}^{k} \left( \begin{array}{*{2}{c}} k \\ \kappa \\ \end{array} \right)\cdot \mu_\kappa \cdot {m_1}^{k-\kappa}.$$

Some Frequently Used Central Moments

Aus der letzten Definition können folgende statistische Kenngrößen abgeleitet werden:

$\text{Definition:}$  Die  Varianz  der betrachteten Zufallsgröße  $X$  ist das Zentralmoment zweiter Ordnung:

$$\mu_2 = {\rm E}\big[(X-m_{\rm 1})^2\big] = \sigma_X^2.$$

• Die Varianz  $σ_X^2$  entspricht physikalisch der "Wechselleistung" und die  Streung  $σ_X$  (oder auch  Standardabweichung) gibt den "Effektivwert" an.
• Aus dem linearen und dem quadratischen Mittelwert ist die Varianz nach dem  Satz von Steiner  in folgender Weise berechenbar:  $\sigma_X^{2} = {\rm E}\big[X^2 \big] - {\rm E}^2\big[X \big].$

$\text{Definition:}$  Die  Charliersche Schiefe  $S_X$  der betrachteten Zufallsgröße  $X$  bezeichnet das auf $σ_X^3$ bezogene dritte Zentralmoment.

• Bei symmetrischer Dichtefunktion ist die Kenngröße  $S_X$  sets Null.
• Je größer  $S_X = \mu_3/σ_X^3$  ist, um so unsymmetrischer verläuft die WDF um den Mittelwert  $m_X$.
• Beispielsweise ergibt sich für die Exponentialverteilung die Schiefe  $S_X =2$, und zwar unabhängig vom Verteilungsparameter  $λ$.

$\text{Definition:}$  Als  Kurtosis  der betrachteten Zufallsgröße  $X$  bezeichnet man den Quotienten  $K_X = \mu_4/σ_X^4$    $(\mu_4:$  Zentralmoment vierter Ordnung$)$.

• Bei einer gaußverteilten Zufallsgröße ergibt sich hierfür immer der Wert  $K_X = 3$.
• Anhand dieser Kenngröße kann man beispielsweise überprüfen, ob eine vorliegende Zufallsgröße tatsächlich gaußisch ist oder zumindest durch eine Gaußverteilung approximiert werden kann.

Compilation of some Continuous–Value Random Variables

Das Applet berücksichtigt folgende Verteilungen: 

Gaußverteilung, Gleichverteilung, Dreieckverteilung, Exponentialverteilung, Laplaceverteilung, Rayleighverteilung,
Riceverteilung, Weibullverteilung, Wigner–Halbkreisverteilung, Wigner–Parabelverteilung, Cauchyverteilung.

Einige von diesen sollen hier detailliert beschrieben werden.

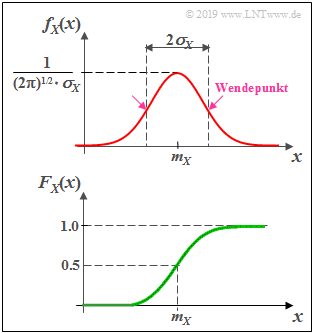
Gaußverteilte Zufallsgrößen

Gaußsche Zufallsgröße:  WDF und VTF

(1)    Wahrscheinlichkeitsdichtefunktion   $($achsensymmetrisch um  $m_X)$

$$f_X(x) = \frac{1}{\sqrt{2\pi}\cdot\sigma_X}\cdot {\rm e}^{-(X-m_X)^2 /(2\sigma_X^2) }.$$

WDF–Parameter: 

• $m_X$  (Mittelwert bzw. Gleichanteil),
• $σ_X$  (Streuung bzw. Effektivwert).

(2)    Verteilungsfunktion   $($punktsymmetrisch um  $m_X)$

$$F_X(x)= \phi(\frac{\it x-m_X}{\sigma_X})\hspace{0.5cm}\rm mit\hspace{0.5cm}\rm \phi (\it x\rm ) = \frac{\rm 1}{\sqrt{\rm 2\it \pi}}\int_{-\rm\infty}^{\it x} \rm e^{\it -u^{\rm 2}/\rm 2}\,\, d \it u.$$

$ϕ(x)$:   Gaußsches Fehlerintegral (nicht analytisch berechenbar, muss aus Tabellen entnommen werden).

(3)    Zentralmomente

$$\mu_{k}=(k- 1)\cdot (k- 3) \ \cdots \ 3\cdot 1\cdot\sigma_X^k\hspace{0.2cm}\rm (falls\hspace{0.2cm}\it k\hspace{0.2cm}\rm gerade).$$

• Charliersche Schiefe  $S_X = 0$,  da  $\mu_3 = 0$  $($WDF ist symmetrisch um  $m_X)$.
• Kurtosis  $K_X = 3$,  da  $\mu_4 = 3 \cdot \sigma_X^2$  ⇒   $K_X = 3$  ergibt sich nur für die Gauß–WDF.

(4)    Weitere Bemerkungen

• Die Namensgebung geht auf den bedeutenden Mathematiker, Physiker und Astronomen Carl Friedrich Gauß zurück.
• Ist  $m_X = 0$  und  $σ_X = 1$, so spricht man oft auch von der  Normalverteilung.

• Die Streuung kann aus der glockenförmigen WDF $f_{X}(x)$ auch grafisch ermittelt werden  (als Abstand von Maximalwert und Wendepunkt).
• Zufallsgrößen mit Gaußscher WDF sind wirklichkeitsnahe Modelle für viele physikalische Größen und auch für die Nachrichtentechnik von großer Bedeutung.
• Die Summe vieler kleiner und unabhängiger Komponenten führt stets zur Gauß–WDF   ⇒   Zentraler Grenzwertsatz der Statistik   ⇒   Grundlage für Rauschprozesse.
• Legt man ein gaußverteiltes Signal zur spektralen Formung an ein lineares Filter, so ist das Ausgangssignal ebenfalls gaußverteilt.

Signal und WDF eines Gaußschen Rauschsignals

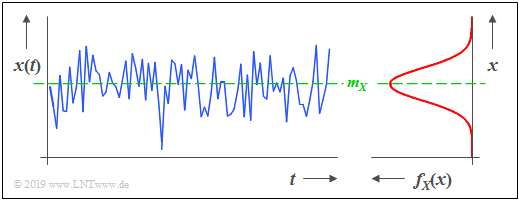
$\text{Beispiel 1:}$  Die Grafik zeigt einen Ausschnitt eines stochastischen Rauschsignals  $x(t)$, dessen Momentanwert als eine kontinuierliche Zufallsgröße  $X$  aufgefasst werden kann. Aus der rechts dargestellten WDF erkennt man:

• Es liegt eine Gaußsche Zufallsgröße vor.
• Momentanwerte um den Mittelwert  $m_X$  treten am häufigsten auf.
• Wenn zwischen den Abtastwerten  $x_ν$  der Folge keine statistischen Bindungen bestehen, bezeichnet man ein solches Signal auch als „Weißes Rauschen”.

Gleichverteilte Zufallsgrößen

Gleichverteilung:  WDF und VTF

(1)    Wahrscheinlichkeitsdichtefunktion

• Die Wahrscheinlichkeitsdichtefunktion (WDF)  $f_{X}(x)$  ist im Bereich von  $x_{\rm min}$  bis  $x_{\rm max}$  konstant gleich  $1/(x_{\rm max} - x_{\rm min})$  und außerhalb Null.
• An den Bereichsgrenzen ist für  $f_{X}(x)$  jeweils nur der halbe Wert  (Mittelwert zwischen links- und rechtsseitigem Grenzwert)  zu setzen.

(2)    Verteilungsfunktion

• Die Verteilungsfunktion (VTF) steigt im Bereich von  $x_{\rm min}$  bis  $x_{\rm max}$  linear von Null auf  $1$  linear an.

(3)    Momente und Zentralmomente

• Mittelwert und Streuung haben bei der Gleichverteilung die folgenden Werte:

$$m_X = \frac{\it x_ {\rm max} \rm + \it x_{\rm min}}{2},\hspace{0.5cm} \sigma_X^2 = \frac{(\it x_{\rm max} - \it x_{\rm min}\rm )^2}{12}.$$

• Bei symmetrischer WDF   ⇒   $x_{\rm min} = -x_{\rm max}$  ist der Mittelwert  $m_X = 0$  und die Varianz  $σ_X^2 = x_{\rm max}^2/3.$
• Aufgrund der Symmetrie um den Mittelwert  $m_X$  ist die Charliersche Schiefe  $S_X = 0$.
• Die Kurtosis ist mit   $K_X = 1.8$  deutlich kleiner als bei der Gaußverteilung, weil die WDF–Ausläufer fehlen.

(4)    Weitere Bemerkungen

• Für die Modellierung übertragungstechnischer Systeme sind gleichverteilte Zufallsgrößen die Ausnahme. Ein Beispiel für eine tatsächlich (nahezu) gleichverteilte Zufallsgröße ist die Phase bei kreissymmetrischen Störungen, wie sie beispielsweise bei  Quadratur–Amplitudenmodulationsverfahren  (QAM) auftreten.

• Die Bedeutung gleichverteilter Zufallsgrößen für die Informations– und Kommunikationstechnik liegt eher darin, dass diese WDF–Form aus Sicht der Informationstheorie unter der Nebenbedingung "Spitzenwertbegrenzung" ein Optimum bezüglich der differentiellen Entropie darstellt.

• In der Bildverarbeitung & Bildcodierung wird häufig mit der Gleichverteilung anstelle der tatsächlichen, meist sehr viel komplizierteren Verteilung des Originalbildes gerechnet, da der Unterschied des Informationsgehaltes zwischen einem natürlichen Bild und dem auf der Gleichverteilung basierenden Modell relativ gering ist.

• Bei der Simulation nachrichtentechnischer Systeme verwendet man häufig auf der Gleichverteilung basierende "Pseudo–Zufallsgeneratoren" (die relativ einfach zu realisieren sind), woraus sich andere Verteilungen  (Gaußverteilung, Exponentialverteilung, etc.)  leicht ableiten lassen.

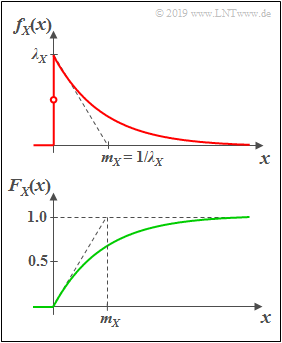
Exponentialverteilte Zufallsgrößen

(1)    Wahrscheinlichkeitsdichtefunktion

Exponentialverteilung:  WDF und VTF

Eine exponentialverteilte Zufallsgröße  $X$  kann nur nicht–negative Werte annehmen. Für  $x>0$  hat die WDF den folgenden Verlauf hat:

$$f_X(x)=\it \lambda_X\cdot\rm e^{\it -\lambda_X \hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$

• Je größer der Verteilungsparameter  $λ_X$  ist, um so steiler erfolgt der Abfall.
• Definitionsgemäß gilt  $f_{X}(0) = λ_X/2$, also der Mittelwert aus linksseitigem Grenzwert  $(0)$  und rechtsseitigem Grenzwert  $(\lambda_X)$.

(2)    Verteilungsfunktion

Durch Integration über die WDF erhält man für  $x > 0$:

$$F_{X}(x)=1-\rm e^{\it -\lambda_X\hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$

(3)    Momente und Zentralmomente

• Die  Momente  der (einseitigen) Exponentialverteilung sind allgemein gleich:

$$m_k = \int_{-\infty}^{+\infty} x^k \cdot f_{X}(x) \,\,{\rm d} x = \frac{k!}{\lambda_X^k}.$$

• Daraus und aus dem Satz von Steiner ergibt sich für Mittelwert und Streuung:

$$m_X = m_1=\frac{1}{\lambda_X},\hspace{0.6cm}\sigma_X^2={m_2-m_1^2}={\frac{2}{\lambda_X^2}-\frac{1}{\lambda_X^2}}=\frac{1}{\lambda_X^2}.$$

• Die WDF ist hier deutlich unsymmetrisch. Für die Charliersche Schiefe ergibt sich  $S_X = 2$.
• Die Kurtosis ist mit   $K_X = 9$  deutlich größer als bei der Gaußverteilung, weil die WDF–Ausläufer sehr viel weiter reichen.

(4)    Weitere Bemerkungen

• Die Exponentialverteilung hat große Bedeutung für Zuverlässigkeitsuntersuchungen; in diesem Zusammenhang ist auch der Begriff "Lebensdauerverteilung" üblich.
• Bei diesen Anwendungen ist die Zufallsgröße oft die Zeit  $t$, die bis zum Ausfall einer Komponente vergeht.
• Desweiteren ist anzumerken, dass die Exponentialverteilung eng mit der Laplaceverteilung in Zusammenhang steht.

Laplaceverteilte Zufallsgrößen

Laplaceverteiung:  WDF und VTF

(1)    Wahrscheinlichkeitsdichtefunktion

Wie aus der Grafik zu ersehen ist die Laplaceverteilung eine "zweiseitige Exponentialverteilung":

$$f_{X}(x)=\frac{\lambda_X} {2}\cdot{\rm e}^ { - \lambda_X \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.05cm} x \hspace{0.05cm} \vert}.$$

• Der Maximalwert ist hier  $\lambda_X/2$.
• Die Tangente bei  $x=0$  schneidet die Abszisse wie bei der Exponentialverteilung bei  $1/\lambda_X$.

(2)    Verteilungsfunktion

$$F_{X}(x) = {\rm Pr}\big [X \le x \big ] = \int_{-\infty}^{x} f_{X}(\xi) \,\,{\rm d}\xi$$

$$\Rightarrow \hspace{0.5cm} F_{X}(x) = 0.5 + 0.5 \cdot {\rm sign}(x) \cdot \big [ 1 - {\rm e}^ { - \lambda_X \hspace{0.05cm} \cdot \hspace{0.05cm} \vert \hspace{0.05cm} x \hspace{0.05cm} \vert}\big ]$$

$$\Rightarrow \hspace{0.5cm} F_{X}(-\infty) = 0, \hspace{0.5cm}F_{X}(0) = 0.5, \hspace{0.5cm} F_{X}(+\infty) = 1.$$

(3)    Momente und Zentralmomente

• Für ungeradzahliges  $k$  ergibt sich bei der Laplaceverteilung aufgrund der Symmetrie stets  $m_k= 0$. Unter Anderem:  Linearer Mittelwert  $m_X =m_1 = 0$.

• Für geradzahliges  $k$  stimmen die Momente von Laplaceverteilung und Exponentialverteilung überein:  $m_k = {k!}/{\lambda^k}$.

• Für die Varianz  $(=$ Zentralmoment zweiter Ordnung $=$ Moment zweiter Ordnung$)$  gilt:  $\sigma_X^2 = {2}/{\lambda_X^2}$   ⇒   doppelt so groß wie bei der Exponentialverteilung.

• Für die Charliersche Schiefe ergibt sich hier aufgrund der symmetrischen WDF   $S_X = 0$.

• Die Kurtosis ist mit  $K_X = 6$  deutlich größer als bei der Gaußverteilung, aber kleiner als bei der Exponentialverteilung.

(4)    Weitere Bemerkungen

• Die Momentanwerte von Sprach– und Musiksignalen sind mit guter Näherung laplaceverteilt.
  Siehe Lernvideo  Wahrscheinlichkeit und Wahrscheinlichkeitsdichtefunktion,  Teil 2.
• Durch eine zusätzliche Diracfunktion bei  $x=0$  lassen sich auch Sprachpausen modellieren.

Kurzbeschreibung weiterer Verteilungen

$\text{(A) Rayleighverteilung}$     Genauere Beschreibung

• Wahrscheinlichkeitsdichtefunktion:

$$f_X(x) = \left\{ \begin{array}{c} x/\lambda_X^2 \cdot {\rm e}^{- x^2/(2 \hspace{0.05cm}\cdot\hspace{0.05cm} \lambda_X^2)} \\ 0 \end{array} \right.\hspace{0.15cm} \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.1cm} x\hspace{-0.05cm} \ge \hspace{-0.05cm}0, \\ {\rm f\ddot{u}r}\hspace{0.1cm} x \hspace{-0.05cm}<\hspace{-0.05cm} 0. \\ \end{array}.$$

• Anwendung:     Modellierung des Mobilfunkkanals (nichtfrequenzselektives Fading, nur Dämpfungs–, Beugungs– und Brechungseffekte, keine Sichtverbindung).

$\text{(B) Riceverteilung}$     Genauere Beschreibung

• Wahrscheinlichkeitsdichtefunktion  $(\rm I_0$  bezeichnet die modifizierte Bessel–Funktion nullter Ordnung$)$:

$$f_X(x) = \frac{x}{\lambda_X^2} \cdot {\rm exp} \big [ -\frac{x^2 + C_X^2}{2\cdot \lambda_X^2}\big ] \cdot {\rm I}_0 \left [ \frac{x \cdot C_X}{\lambda_X^2} \right ]\hspace{0.5cm}\text{mit}\hspace{0.5cm}{\rm I }_0 (u) = {\rm J }_0 ({\rm j} \cdot u) = \sum_{k = 0}^{\infty} \frac{ (u/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.$$

• Anwendung:     Modellierung des Mobilfunkkanals (nichtfrequenzselektives Fading, nur Dämpfungs–, Beugungs– und Brechungseffekte, mit Sichtverbindung).

$\text{(C) Weibullverteilung}$     [Genauere Beschreibung]

• Wahrscheinlichkeitsdichtefunktion:

$$f_X(x) = \lambda_X \cdot k_X \cdot (\lambda_X \cdot x)^{k_X-1} \cdot {\rm e}^{(\lambda_X \cdot x)^{k_X}} \hspace{0.05cm}.$$

• Anwendung:     WDF mit einstellbarer Schiefe $S_X$; Exponentialverteilung  $(k_X = 1)$  und Rayleighverteilung  $(k_X = 2)$  als Sonderfälle enthalten.

$\text{(D) Wigner-Halbkreisverteilung}$     [Genauere Beschreibung]

• Wahrscheinlichkeitsdichtefunktion:

$$f_X(x) = \left\{ \begin{array}{c} 2/(\pi \cdot {R_X}^2) \cdot \sqrt{{R_X}^2 - (x- m_X)^2} \\ 0 \end{array} \right.\hspace{0.15cm} \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.1cm} |x- m_X|\hspace{-0.05cm} \le \hspace{-0.05cm}R_X, \\ {\rm f\ddot{u}r}\hspace{0.1cm} |x- m_X| \hspace{-0.05cm} > \hspace{-0.05cm} R_X \\ \end{array}.$$

• Anwendung:     WDF der Tschebyscheff–Knoten   ⇒   Nullstellen der Tschebyscheff–Polynome aus der Numerik.

$\text{(E) Wigner-Parabelverteilung}$

• Wahrscheinlichkeitsdichtefunktion:

$$f_X(x) = \left\{ \begin{array}{c} 3/(4 \cdot {R_X}^3) \cdot \big ({R_X}^2 - (x- m_X)^2\big ) \\ 0 \end{array} \right.\hspace{0.15cm} \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.1cm} |x|\hspace{-0.05cm} \le \hspace{-0.05cm}R_X, \\ {\rm f\ddot{u}r}\hspace{0.1cm} |x| \hspace{-0.05cm} > \hspace{-0.05cm} R_X \\ \end{array}.$$

• Anwendung:     WDF der Eigenwerte von symmetrischen Zufallsmatrizen, deren Dimension gegen unendlich geht.

$\text{(F) Cauchyverteilung}$     Genauere Beschreibung

• Wahrscheinlichkeitsdichtefunktion und Verteilungsfunktion:

$$f_{X}(x)=\frac{1}{\pi}\cdot\frac{\lambda_X}{\lambda_X^2+x^2}, \hspace{2cm} F_{X}(x)={\rm 1}/{2}+{\rm arctan}({x}/{\lambda_X}).$$

• Bei der Cauchyverteilung besitzen alle Momente  $m_k$  für gerades  $k$  einen unendlich großen Wert, und zwar unabhängig vom Parameter  $λ_X$.
• Damit besitzt diese Verteilung auch eine unendlich große Varianz:  $\sigma_X^2 \to \infty$.
• Aufgrund der Symmetrie sind für ungerades  $k$  alle Momente  $m_k = 0$, wenn man wie im Programm vom "Cauchy Principal Value" ausgeht:  $m_X = 0, \ S_X = 0$.
• Beispiel:     Der Quotient zweier Gaußscher mittelwertfreier Zufallsgrößen ist cauchyverteilt. Für praktische Anwendungen hat die Cauchyverteilung weniger Bedeutung.

Exercises

• First, select the number  $(1,\ 2, \text{...} \ )$  of the task to be processed.  The number  "$0$"  corresponds to a  "Reset":  Same setting as at program start.
• A task description is displayed.  The parameter values are adjusted.  Solution after pressing  "Show Solution".
• In the following  $\text{Red}$  stands for the random variable  $X$  and  $\text{Blue}$  for  $Y$.

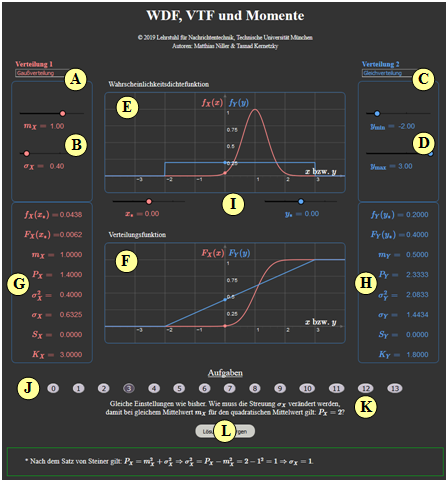
(1)  Select  $\text{red: Gaussian PDF}\ (m_X = 1, \ \sigma_X = 0.4)$  and  $\text{blue: Rectangular PDF}\ (y_{\rm min} = -2, \ y_{\rm max} = +3)$.  Interpret the  $\rm PDF$  graph.

•  $\text{Gaussian PDF}$:  The  $\rm PDF$ maximum is equal to  $f_{X}(x = m_X) = \sqrt{1/(2\pi \cdot \sigma_X^2)} = 0.9974 \approx 1$.
•  $\text{Rectangular PDF}$:  All  $\rm PDF$ values are equal  $0.2$  in the range  $-2 < y < +3$.  At the edges  $f_Y(-2) = f_Y(+3)= 0.1$  (half value) holds.

(2)  Same setting as for  $(1)$.  What are the probabilities  ${\rm Pr}(X = 0)$,   ${\rm Pr}(0.5 \le X \le 1.5)$,   ${\rm Pr}(Y = 0)$   and  ${\rm Pr}(0.5 \le Y \le 1.5)$ .

•  ${\rm Pr}(X = 0)={\rm Pr}(Y = 0) \equiv 0$   ⇒   Probability of a discrete random variable to take exactly a certain value.
•  The other two probabilities can be obtained by integration over the PDF in the range  $+0.5\ \text{...} \ +\hspace{-0.1cm}1.5$.
•  Or:  ${\rm Pr}(0.5 \le X \le 1.5)= F_X(1.5) - F_X(0.5) = 0.8944-0.1056 = 0.7888$. Correspondingly:  ${\rm Pr}(0.5 \le Y \le 1.5)= 0.7-0.5=0.2$.

(3)  Same settings as before.  How must the standard deviation  $\sigma_X$  be changed so that with the same mean  $m_X$  it holds for the quadratic mean:  $P_X=2$ ?

•  According to Steiner's theorem:  $P_X=m_X^2 + \sigma_X^2$   ⇒   $\sigma_X^2 = P_X-m_X^2 = 2 - 1^2 = 1$   ⇒   $\sigma_X = 1$.

(4)  Same settings as before:  How must the parameters  $y_{\rm min}$  and  $y_{\rm max}$  of the rectangular PDF be changed to yield  $m_Y = 0$  and  $\sigma_Y^2 = 0.75$?

•  Starting from the previous setting  $(y_{\rm min} = -2, \ y_{\rm max} = +3)$  we change  $y_{\rm max}$ until  $\sigma_Y^2 = 0.75$  occurs   ⇒   $y_{\rm max} = 1$.
•  The width of the rectangle is now  $3$.  The desired mean   $m_Y = 0$  is obtained by shifting:  $y_{\rm min} = -1.5, \ y_{\rm max} = +1.5$.
•  You could also consider that for a mean-free random variable  $(y_{\rm min} = -y_{\rm max})$  the following equation holds:   $\sigma_Y^2 = y_{\rm max}^2/3$.

(5)  For which of the adjustable distributions is the Charlier skewness  $S \ne 0$ ?

•  The Charlier's skewness denotes the third central moment related to  $σ_X^3$   ⇒  $S_X = \mu_3/σ_X^3$  $($valid for the random variable  $X)$.
•  If the PDF  $f_X(x)$  is symmetric around the mean  $m_X$  then the parameter  $S_X$  is always zero.
•  Exponential distribution:  $S_X =2$;  Rayleigh distribution:  $S_X =0.631$   $($both independent of  $λ_X)$;   Rice distribution:  $S_X >0$  $($dependent of  $C_X, \ λ_X)$.
•  With the Weibull distribution, the Charlier skewness  $S_X$  can be zero, positive or negative,  depending on the PDF parameter  $k_X$.
•   Weibull distribution,  $\lambda_X=0.4$:  With  $k_X = 1.5$  ⇒   PDF is curved to the left  $(S_X > 0)$;   $k_X = 7$  ⇒   PDF is curved to the right  $(S_X < 0)$.

(6)  Select  $\text{Red: Gaussian PDF}\ (m_X = 1, \ \sigma_X = 0.4)$  and  $\text{Blue: Gaussian PDF}\ (m_X = 0, \ \sigma_X = 1)$.  What is the kurtosis in each case?

•  For each Gaussian distribution the kurtosis has the same value:   $K_X = K_Y =3$.  Therefore,  $K-3$  is called "excess".
• This parameter can be used to check whether a given random variable can be approximated by a Gaussian distribution.

(7)  For which distributions does a significantly smaller kurtosis value result than  $K=3$?  And for which distributions does a significantly larger one?

•  $K<3$  always results when the PDF values are more concentrated around the mean than in the Gaussian distribution.
•  This is true, for example, for the uniform distribution  $(K=1.8)$  and for the triangular distribution  $(K=2.4)$.
•  $K>3$,  if the PDF offshoots are more pronounced than for the Gaussian distribution.  Example:  Exponential PDF  $(K=9)$.

(8)  Select  $\text{Red: Exponential PDF}\ (\lambda_X = 1)$  and  $\text{Blue: Laplace PDF}\ (\lambda_Y = 1)$.  Interpret the differences.

•  The Laplace distribution is symmetric around its mean  $(S_Y=0, \ m_Y=0)$  unlike the exponential distribution  $(S_X=2, \ m_X=1)$.
•  The even moments  $m_2, \ m_4, \ \text{...}$  are equal,  for example:  $P_X=P_Y=2$.  But not the variances:  $\sigma_X^2 =1, \ \sigma_Y^2 =2$.
•  The probabilities  ${\rm Pr}(|X| < 2) = F_X(2) = 0.864$  and  ${\rm Pr}(|Y| < 2) = F_Y(2) - F_Y(-2)= 0.932 - 0.068 = 0.864$  are equal.
•  In the Laplace PDF, the values are more tightly concentrated around the mean than in the exponential PDF:  $K_Y =6 < K_X = 9$.

(9)  Select  $\text{Red: Rice PDF}\ (\lambda_X = 1, \ C_X = 1)$  and  $\text{Blue: Rayleigh PDF}\ (\lambda_Y = 1)$.  Interpret the differences.

•   With  $C_X = 0$  the Rice PDF transitions to the Rayleigh PDF.  A larger  $C_X$  improves the performance, e.g., in mobile communications.
•   Both, in  "Rayleigh"  and  "Rice"  the abscissa is the magnitude  $A$  of the received signal.  Favorably, if  ${\rm Pr}(A \le A_0)$  is small  $(A_0$  given$)$.
•   For  $C_X \ne 0$  and equal  $\lambda$  the Rice CDF is below the Rayleigh CDF   ⇒   smaller  ${\rm Pr}(A \le A_0)$  for all  $A_0$.

(10)  Select  $\text{Red: Rice PDF}\ (\lambda_X = 0.6, \ C_X = 2)$.  By which distribution  $F_Y(y)$  can this Rice distribution be well approximated?

•   The kurtosis   $K_X = 2.9539 \approx 3$  indicates the Gaussian distribution.   Favorable parameters:  $m_Y = 2.1 > C_X, \ \ \sigma_Y = \lambda_X = 0.6$.
•   The larger tht quotient  $C_X/\lambda_X$  is, the better the Rice PDF is approximated by a Gaussian PDF.
•   For large   $C_X/\lambda_X$  the Rice PDF has no more similarity with the Rayleigh PDF.

(11)  Select  $\text{Red: Weibull PDF}\ (\lambda_X = 1, \ k_X = 1)$  and  $\text{Blue: Weibull PDF}\ (\lambda_Y = 1, \ k_Y = 2)$. Interpret the results.

•   The Weibull PDF  $f_X(x)$  is identical to the exponential PDF and  $f_Y(y)$  to the Rayleigh PDF.
•   However, after best fit, the parameters  $\lambda_{\rm Weibull} = 1$  and  $\lambda_{\rm Rayleigh} = 0.7$ differ.
•   Moreover, it holds  $f_X(x = 0) \to \infty$  for  $k_X < 1$.  However, this does not have the affect of infinite momenta.

(12)  Select  $\text{Red: Weibull PDF}\ (\lambda_X = 1, \ k_X = 1.6)$  and   $\text{Blue: Weibull PDF}\ (\lambda_Y = 1, \ k_Y = 5.6)$.  Interpret the Charlier skewness.

•   One observes:   For the PDF parameter  $k < k_*$  the Charlier skewness is positive and for  $k > k_*$  negative.  It is approximately  $k_* = 3.6$.

(13)  Select  $\text{Red: Semicircle PDF}\ (m_X = 0, \ R_X = 1)$  and  $\text{Blue: Parabolic PDF}\ (m_Y = 0, \ R_Y = 1)$.  Vary the parameter  $R$  in each case.

•   The PDF in each case is mean-free and symmetric  $(S_X = S_Y =0)$  with  $\sigma_X^2 = 0.25, \ K_X = 2$  respectively,  $\sigma_Y^2 = 0.2, \ K_Y \approx 2.2$.

Applet Manual

Screenshot of the German version

    (A)     Auswahl der Verteilung  $f_X(x)$  (rote Kurven und Ausgabewerte)

    (B)     Parametereingabe für die "rote Verteilung" per Slider

    (C)     Auswahl der Verteilung  $f_Y(y)$  (blaue Kurven und Ausgabewerte)

    (D)     Parametereingabe für die "rote Verteilung" per Slider

    (E)     Grafikbereich für die Wahrscheinlichkeitsdichtefunktion (WDF)

    (F)     Grafikbereich für die Verteilungsfunktion (VTF)

    (G)     Numerikausgabe für die "rote Verteilung"

    (H)     Numerikausgabe für die "blaue Verteilung"

    ( I )     Eingabe der Abszissenwerte  $x_*$  und  $y_*$  für die Numerik–Ausgaben

    (J)     Bereich für die Versuchsdurchführung:   Aufgabenauswahl

    (K)     Bereich für die Versuchsdurchführung:   Aufgabenstellung

    ( L)     Bereich für die Versuchsdurchführung:   Musterlösung

Auswahlmöglichkeiten für  $\rm A$  und  $\rm C$:  

Gaußverteilung,   Gleichverteilung,   Dreieckverteilung,   Exponentialverteilung,   Laplaceverteilung,   Rayleighverteilung,  Riceverteilung,   Weibullverteilung,   Wigner–Halbkreisverteilung,   Wigner–Parabelverteilung,   Cauchyverteilung.

Folgende integrale Kenngrößen werden ausgegeben  $($bzgl. $X)$:  

Linearer Mittelwert  $m_X = {\rm E}\big[X \big]$,   quadratischer Mittelwert  $P_X ={\rm E}\big[X^2 \big]$,   Varianz  $\sigma_X^2 = P_X - m_X^2$,   Standardabweichung (oder Streuung)  $\sigma_X$,  Charliersche Schiefe  $S_X$,   Kurtosis  $K_X$.

In all applets top right:    Changeable graphical interface design   ⇒   Theme:

• Dark:   black background  (recommended by the authors).
• Bright:   white background  (recommended for beamers and printouts)
• Deuteranopia:   for users with pronounced green–visual impairment
• Protanopia:   for users with pronounced red–visual impairment

About the Authors

This interactive calculation tool was designed and implemented at the  Institute for Communications Engineering  at the  Technical University of Munich.

• The first version was created in 2005 by  Bettina Hirner  as part of her diploma thesis with “FlashMX – Actionscript”  (Supervisor:  Günter Söder  and  Klaus Eichin).

• In 2019 the program was redesigned via HTML5/JavaScript by  Matthias Niller  (Ingenieurspraxis Mathematik, Supervisor:  Benedikt Leible  and  Tasnád Kernetzky ).

• Last revision and English version 2021 by  Carolin Mirschina  in the context of a working student activity.  Translation using DEEPL.com (free version).

• The conversion of this applet was financially supported by  "Studienzuschüsse"  (TUM Department of Electrical and Computer Engineering).  We thank.

Once again: Open Applet in new Tab

Open Applet in new Tab   Deutsche Version Öffnen