Exercise 1.4Z: Sum of Ternary Quantities

• Return to book

Gegeben seien die ternären Zufallsgrößen

• $x ∈ {–2, 0, +2}$,

• $y ∈ {–1, 0, +1}$.

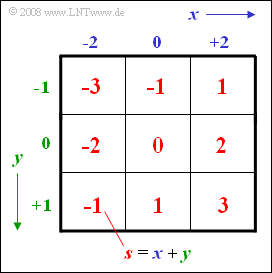
Diese beiden Ternärwerte treten jeweils mit gleicher Wahrscheinlichkeit auf. Daraus wird als eine neue Zufallsgröße die Summe $s = x + y$ gebildet.

Nebenstehendes Schema zeigt, dass die Summe s alle ganzzahligen Werte zwischen –3 und +3 annehmen kann $$s \in \{-3, -2, -1, 0, +1, +2, +3\}$$ ,

Hinweis: Diese Aufgabe bezieht sich auf den Lehrstoff von Kapitel 1.3. Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das nachfolgende Lernvideo:

Fragebogen

1

Berechnen Sie die Wahrscheinlichkeit, dass die Summe $s$ positv ist:

$Pr(s>0)$ =

2

Berechnen Sie die Wahrscheinlichkeit, dass sowohl die Eingangsgröße x als auch die Summe s positiv sind:

$Pr((x>0) \cap (s>0))$ =

3

Berechnen Sie die bedingte Wahrscheinlichkeit, dass die Eingangsgröße x > 0 ist, wenn s > 0 gilt:

$Pr(x>0|s>0)$ =

4

Berechnen Sie die bedingte Wahrscheinlichkeit, dass die Summe s positiv ist, wenn die Eingangsgröße x > 0 ist:

$Pr(s>0|x>0)$ =

Musterlösung

Solution

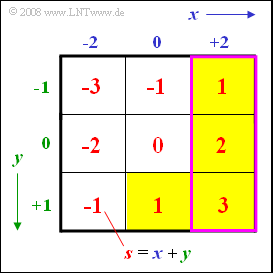
In der nebenstehenden Grafik sind die drei zum Ereignis $„x > 0“$ gehörenden Felder violett umrandet, während die Felder für $„s > 0“$ gelb hinterlegt sind. Alle gesuchten Wahrscheinlichkeiten können hier mit Hilfe der klassischen Definition ermittelt werden.

1.  Dieses Ereignis ist durch die gelb hinterlegten Felder gekennzeichnet:

$$\rm Pr (\it s > \rm 0) = \rm 4/9 \hspace{0.15cm}\underline { \approx \rm 0.444}.$$

2.  Hier gilt folgender Sachverhalt:

$$\rm Pr((\it x > \rm 0) \cap (\it s>\rm 0) ) = \rm Pr(\it x > \rm 0) =\rm 3/9\hspace{0.15cm}\underline { \approx \rm 0.333}.$$

3.  Mit den Ergebnissen aus (a) und (b) folgt:

$$\rm Pr(\it x > \rm 0 \hspace{0.05cm}| \hspace{0.05cm} \it s > \rm 0) = \frac{{\rm Pr} ((\it x > \rm 0) \cap (\it s > \rm 0))}{{\rm Pr}(\it s > \rm 0)}= \frac{3/9}{4/9}\hspace{0.15cm}\underline {= 0.75}.$$

4.  Analog zur Teilfrage (c) gilt nun:

$$\rm Pr(\it s > \rm 0 \hspace{0.05cm} | \hspace{0.05cm} \it x > \rm 0)=\frac{Pr((\it x > \rm 0) \cap (\it s > \rm 0))}{Pr(\it x >\rm 0)}=\rm \frac{3/9}{3/9}\hspace{0.15cm}\underline {= 1}.$$