Exercise 1.5Z: Symmetrical Markov Source
From LNTwww
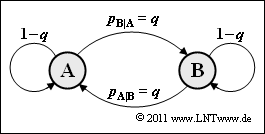
- In der Aufgabe A1.5 wurde eine binäre Markovquelle behandelt, bei der die Übergangswahrscheinlichkeiten von A nach B sowie von B nach A unterschiedlich waren. In dieser Aufgabe soll nun gelten:
- pA|B=pB|A=q(0≤q≤1).
- Alle in der Aufgabe A1.5 angegebenen Gleichungen gelten auch hier:
- Entropie:
- H=pAA⋅ld1pA|A+pAB⋅ld1pB|A+pBA⋅ld1pA|B+pBB⋅ld1pB|B,
- Erste Entropienäherung:
- H1=pA⋅ld1pA+pB⋅ld1pB,
- k–te Entropienäherung (k = 2, 3, ...):
- Hk=1k⋅[H1+(k−1)⋅H],H=lim
- Hinweis: Die Aufgabe bezieht sich auf Kapitel 1.2, Seite 5c. Bei allen Entropien ist die Pseudoeinheit „bit/Symbol” hinzuzufügen.
Fragebogen
Musterlösung
- 1. Bei einer stationären binären Markovquelle erster Ordnung gilt:
- p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} + p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} = (1-q) \cdot p_{\rm A} + q \cdot p_{\rm B}
- q \cdot p_{\rm A} = q \cdot p_{\rm B} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm A} = p_{\rm B}\hspace{0.15cm} \underline {= 0.5} \hspace{0.05cm}.
- 2. Zur Berechnung von H benötigt man alle vier Verbundwahrscheinlichkeiten:
- p_{\rm AA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = 1/2 \cdot(1-q) = p_{\rm BB}\hspace{0.05cm},\\ p_{\rm AB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = 1/2 \cdot q = p_{\rm BA}\hspace{0.05cm}.
- Setzt man diese Werte in die gegebene Entropie–Gleichung ein, so erhält man
- H \hspace{0.1cm} = \hspace{0.1cm} 2 \cdot \frac{1}{2} \cdot(1-q) \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{1-q} + 2 \cdot \frac{1}{2} \cdot q \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{q} = \\ \hspace{0.1cm} = \hspace{0.1cm} q \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{q} + (1-q) \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{1-q} = H_{\rm bin}(q) \hspace{0.05cm}.
- Der gesuchte Zahlenwert ist H = Hbin (0.25) = 0.811 bit/Symbol.
- 3. Bei gleichwahrscheinlichen Binärsymbolen ist H1 = 1 bit/Symbol. Mit der für Markovquellen gültigen Gleichung gilt weiter:
- H_2 \hspace{0.1cm} = \hspace{0.1cm} \frac{1}{2} \cdot [ H_1 + H] \hspace{0.15cm} \underline {= 0.906 \,{\rm bit/Symbol}} \hspace{0.05cm},\\ H_3 \hspace{0.1cm} = \hspace{0.1cm} \frac{1}{3} \cdot [ H_1 + 2 H] \hspace{0.15cm} \underline {= 0.874 \,{\rm bit/Symbol}} \hspace{0.05cm}.
- 4. Das Maximum der binären Entropiefunktion ergibt sich für q = 0.5. Damit beträgt die maximale Entropie H = 1 bit/Symbol. Man erkennt aus der Beziehung H = H1 und aus dem vorne abgebildeten Übergangsdiagramm, dass q = 0.5 statistisch unabhängige Symbole zur Folge hat:
- p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = 0.5 \hspace{0.05cm}, \hspace{0.2cm} p_{\rm B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}= 0.5 \hspace{0.05cm}.
- 5. Richtig sind die Lösungsvorschläge 1 und 2. Die Symbolfolge ergibt sich entweder zu AAAAAA... oder zu BBBBBB..., je nachdem, welches Symbol als Startwert vorgegeben wurde. Die Entropie einer solchen Quelle ist H = Hbin(0) = 0.
- 6. Nun kann weder A direkt auf A noch B direkt auf B folgen. Es ergibt sich eine alternierende Folge, je nach Startwert die Folge ABABAB... oder BABABA... ⇒ Lösungsvorschlag 3. Diese Quelle hat in beiden Fällen ebenfalls die Entropie H = 0 = Hbin(1).
