Contents
Transinformation zwischen wertkontinuierlichen Zufallsgrößen
Im Kapitel 3.3 wurde die Transinformation (englisch: Mutual Information) zwischen den beiden wertdiskreten Zufallsgrößen X und Y unter Anderem in folgender Form angegeben:
I(X;Y)=∑(x,y)∈supp(PXY)PXY(x,y)⋅logPXY(x,y)PX(x)⋅PY(y).
Diese Gleichung entspricht gleichzeitig der Kullback–Leibler–Distanz (kurz KLD) zwischen der Verbundwahrscheinlichkeitsfunktion PXY und dem Produkt der beiden Einzel–PMFs PX und PY :
I(X;Y)=D(PXY||PX⋅PY).
Um daraus die Transinformation I(X;Y) zwischen zwei wertkontinuierlichen Zufallsgrößen X und Y abzuleiten, geht man wie folgt vor (Hochkommata weisen auf quantisierte Größen hin):
- Man quantisiert die Zufallsgrößen X und Y (mit den Quantisierungsintervallen Δx und Δy) und erhält so die Wahrscheinlichkeitsfunktionen P_{X′} und P_{Y′} .
- Die „Vektoren” P_{X′} und P_{Y′} werden nach den Grenzübergängen Δx → 0, Δy → 0 unendlich lang, und auch die Verbund–PMF P_{X′Y′} ist in der Fläche unendlich weit ausgedehnt.
- Durch diese Grenzübergänge ergeben sich die Wahrscheinlichkeitsdichtefunktionen der drei kontinuierlichen Zufallsgrößen entsprechend den folgenden Gleichungen:
f_X(x_{\mu}) = \frac{P_{X'}(x_{\mu})}[[:Template:\it \Delta x]] \hspace{0.05cm}, \hspace{0.3cm}f_Y(y_{\mu}) = \frac{P_{Y'}(y_{\mu})}[[:Template:\it \Delta y]] \hspace{0.05cm}, \hspace{0.3cm}f_{XY}(x_{\mu}\hspace{0.05cm}, y_{\mu}) = \frac{P_{X'Y'}(x_{\mu}\hspace{0.05cm}, y_{\mu})}{{\it \Delta_x} \cdot {\it \Delta_y}} \hspace{0.05cm}.
- Aus der Doppelsumme in der obigen Gleichung wird nach der Umbenennung Δx → d_x bzw. Δy → d_y die für wertkontinuierliche Zufallsgrößen gültige Gleichung:
I(X;Y) = \hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ f_{XY}(x, y) } {f_{X}(x) \cdot f_{Y}(y)} \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y \hspace{0.05cm}.
Durch Aufspaltung dieses Doppelintegrals lässt für die Transinformation auch schreiben:
I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.
Verwendet ist hierbei die differentielle Verbund–Entropie
h(XY) = -\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} [f_{XY}(x, y) ] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y
sowie die beiden differentiellen Einzel–Entropien
h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x \hspace{0.05cm},\hspace{0.5cm} h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} [f_Y(y)] \hspace{0.1cm}{\rm d}y \hspace{0.05cm}.
Wir gehen weiter von der wertkontinuierlichen Transinformationsgleichung aus:
I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.
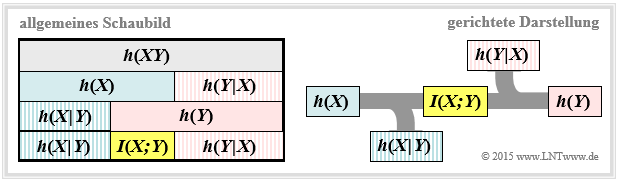
Diese Darstellung findet sich auch im folgenden Schaubild (linke Grafik, über alle Zeilen).
Daraus erkennt man, dass die Transinformation auch noch wie folgt dargestellt werden kann:
I(X;Y) = h(Y) - h(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) =h(X) - h(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}.
Diese fundamentalen informationstheoretischen Zusammenhänge kann man auch aus der rechten Grafik ablesen. Diese gerichtete Darstellung ist für Nachrichtenübertragungssysteme besonders geeignet. Die abfließende bzw. zufließende differentielle Entropie kennzeichnet
- die Äquivokation (englisch: Equivocation):
h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) =\hspace{0.2cm} -\int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \left [{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \right] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm},
- die Irrelevanz (englisch: Irrelevance):
h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) =\hspace{0.2cm}- \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \left [{f_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)} \right] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.
Auf die Bedeutung dieser beiden informationstheoretischen Größen wird in Aufgabe Z4.5 noch genauer eingegangen. Vergleicht man die grafischen Darstellungen der Transinformation bei
- wertdiskreten Zufallsgrößen im Kapitel 3.3 und
- wertkontinuierlichen Zufallsgrößen entsprechend obiger Grafik,
so erkennt man als einziges Unterscheidungsmerkmal, dass jedes „H” (Entropie; größer/gleich Null) durch ein „h” (differentielle Entropie, kann positiv, negativ oder 0 sein) ersetzt wurde. Ansonsten ist die Transinformation in beiden Darstellungen gleich und es gilt stets I(X; Y) ≥ 0. Im Folgenden verwenden wir meist den Logarithmus dualis ⇒ „log2” und erhalten somit die Transinformation in „bit”.
Transinformationsberechnung bei additiver Störung
Wir betrachten nun ein sehr einfaches Modell der Nachrichtenübertragung.
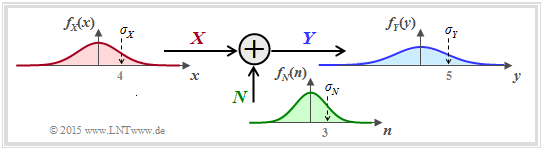
- Die Zufallsgröße X steht für das (mittelwertfreie) Sendesignal und ist durch die WDF f_X(x) und die Varianz σ_X^2 gekennzeichnet. Die Sendeleistung P_X ist identisch mit σ_X^2.
- Die additive Störung N ist durch die WDF f_N(n) und die Störleistung P_N = σ_N^2 gegeben. Da X und N als statistisch unabhängig angenommen werden, gilt \text{E}[X · N] = \text{E}[X] · \text{E}[N] = 0 .
- Das Empfangssignal ist Y = X + N Die Ausgangs–WDF f_Y(y) ist mit der Faltungsoperation berechenbar ⇒ f_Y(y) = f_X(x) ∗ f_N(n) und für die Empfangsleistung (Varianz) gilt:
P_Y = \sigma_Y^2 = {\rm E}[Y^2] = {\rm E}[(X+N)^2] = {\rm E}[X^2] + {\rm E}[N^2] = \sigma_X^2 + \sigma_N^2 = P_X + P_N \hspace{0.05cm}.
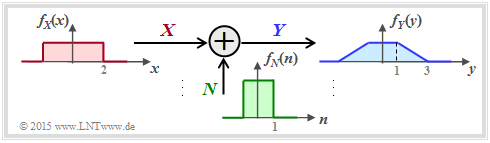
Die in der nachfolgenden Grafik eingezeichneten Dichtefunktionen (rechteck– bzw. trapezförmig) sollen nur den Rechengang verdeutlichen und haben keine praktische Relevanz.
Zur Berechnung der Transinformation zwischen dem Eingang X und dem Ausgang Y gibt es entsprechend dem Schaubild auf der vorherigen Seite drei Möglichkeiten: I(X, Y) = h(X) + h(Y) – h(XY): Die beiden ersten Terme sind aus f_X(x) bzw. f_Y(y) in einfacher Weise berechenbar. Problematisch ist die differentielle Verbundentropie h(XY). Hierzu benötigt man die 2D–Verbund–WDF f_{XY}(x, y), die meist nicht direkt gegeben ist. I(X, Y) = h(Y) – h(Y|X): h(Y|X) bezeichnet die differentielle Streuentropie. Es gilt h(Y|X) = h(X + N|X) = h(N), so dass I(X; Y) bei Kenntnis von f_X(x) und f_N(n) über die Gleichung f_Y(y) = f_X(x) ∗ f_N(n) sehr einfach zu berechnen ist. I(X, Y) = h(X) – h(X|Y): Nach dieser Gleichung benötigt man allerdings die differentielle Rückschlussentropie h(X|Y), die schwieriger angebbar ist als h(Y|X).
Resümée: Im Folgenden schreiben wir für die Transinformation zwischen dem Eingang X und dem Ausgang Y eines Nachrichtenübertragungssystems bei additiver und unkorrelierter Störung N:
I(X;Y) \hspace{-0.05cm} = \hspace{-0.01cm} h(Y) \hspace{-0.01cm}- \hspace{-0.01cm}h(N) \hspace{-0.01cm}=\hspace{-0.05cm} -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.65cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} [f_Y(y)] \hspace{0.1cm}{\rm d}y +\hspace{-0.7cm} \int\limits_{n \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_N)} \hspace{-0.65cm} f_N(n) \cdot {\rm log} \hspace{0.1cm} [f_N(n)] \hspace{0.1cm}{\rm d}n\hspace{0.05cm}.
Kanalkapazität des AWGN–Kanals
Spezifiziert man im bisherigen Systemmodell die Wahrscheinlichkeitsdichtefunktion der Störung (bzw. des Rauschens) zu
f_N(n) = \frac{1}{\sqrt{2\pi \sigma_N^2}} \cdot {\rm exp}\left [ - \hspace{0.05cm}\frac{n^2}{2 \sigma_N^2} \right ] \hspace{0.5cm} {\rm mit } \hspace{0.5cm}\sigma_N^2 = P_N\hspace{0.05cm},
so erhalten wir das folgende Modell zur Berechnung der Kanalkapazität des AWGN–Kanals (Additive White Gaussian Noise).
Die Kanalkapazität C gibt die maximale Transinformation I(X; Y) zwischen der Eingangsgröße X und der Ausgangsgröße Y des AWGN–Kanals an. Die Maximierung bezieht sich dabei auf die bestmögliche Eingangs–WDF. Somit gilt unter der Nebenbedingung der Leistungsbegrenzung:
C = \max_{f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.35cm} I(X;Y) = -h(N) + \max_{f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.35cm} h(Y) \hspace{0.05cm}.
Hier ist bereits berücksichtigt, dass sich die Maximierung allein auf h(Y) ⇒ WDF f_Y(y) bezieht. Bei gegebener Störleistung P_N ist nämlich h(N) = 1/2 · \log2_ (2πe · P_N) eine Konstante.
- Das Maximum für h(Y) erhält man für eine Gaußsche WDF f_Y(y), wobei P_Y = P_X + P_N zu setzen ist, siehe Kapitel 4.1 ⇒ Max [h(Y)] = 1/2 · \log_2 [2πe · (P_X + P_N)].
- Die Ausgangs–WDF f_Y(y) = f_X(x) ∗ f_N(n) ist aber nur dann gaußförmig, wenn sowohl f_X(x) als auch f_N(n) Gaußfunktionen sind. Ein plakativer Merkspruch zur Faltungsoperation lautet nämlich: „Gauß bleibt Gauß, und Nicht–Gauß wird nie (exakt) Gauß”.
Resümée: Beim AWGN–Kanal ⇒ Gaußsche WDF f_N(n) ergibt sich die Kanalkapazität C genau dann, wenn die Eingangs–WDF f_X(x) ebenfalls gaußförmig ist:
C_{\rm AWGN} = h_{\rm max}(Y) - h(N) = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_Y}{P_N} = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X}{P_N}) \hspace{0.05cm}.
Die folgende Tabelle zeigt die AWGN–Kanalkapazität für verschiedene Quotienten P_X/P_N.
Parallele Gaußsche Kanäle
Wir betrachten nun K parallele Gaußkanäle entsprechend der nebenstehenden Grafik
- von X_1 → Y_1, ... , von X_k → Y_k, ... , von X_K → Y_K.
- Die Sendeleistungen in den K Kanälen nennen wir P_1 = \text{E}[X_1^2], ... , P_k = \text{E}[X_k^2], ... , P_K = \text{E}[X_K^2].
- Die K Störleistungen σ_1^2, ... , σ_k^2, ... , σ_K^2 können ebenfalls unterschiedlich sein.
Gesucht ist nun die maximale Transinformation
I(X_1, ... \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, ... \hspace{0.05cm}, Y_K)
- zwischen den K Eingangsgrößen X_1, ... , X_K, sowie
- den K Ausgangsgrößen Y_1, ... , Y_K,
die wir als die Gesamt–Kanalkapazität dieser AWGN–Konfiguration bezeichnen. Dabei gehen wir von Leistungsbegrenzung des Gesamtsystems aus, das heißt, dass die Summe aller Leistungen P_k in den K Einzelkanälen den vorgegebenen Wert P_X nicht überschreiten darf:
P_1 + ... \hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.
Unter der nur wenig einschränkenden Annahme unabhängiger Störquellen N_1, ... , N_K kann für die Transinformation nach einigen Zwischenschritten geschrieben werden:
I(X_1, ... \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, ... \hspace{0.05cm}, Y_K) = h(Y_1, ... \hspace{0.05cm}, Y_K ) - \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} h(N_k)\hspace{0.05cm}.
Dafür kann folgende obere Schranke angegeben werden:
I(X_1, ... \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, ... \hspace{0.05cm}, Y_K) \hspace{0.2cm} \le \hspace{0.1cm} \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} [h(Y_k - h(N_k)] \hspace{0.2cm} \le \hspace{0.1cm} 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_k}{\sigma_k^2}) \hspace{0.05cm}.
- Das Gleichheitszeichen (Identität) gilt bei mittelwertfreien Gaußschen Eingangsgrößen X_k sowie bei statistisch voneinander unabhängigen Störungen N_k.
- Man kommt von dieser Gleichung zur maximalen Transinformation ⇒ Kanalkapazität, wenn man die gesamte Sendeleistung P_X unter Berücksichtigung der unterschiedlichen Störungen in den einzelnen Kanälen ( σ_k^2 ) bestmöglich aufteilt.
- Dieses Optimierungsproblem lässt sich wieder mit dem Verfahren der Lagrange–Multiplikatoren elegant lösen. Das Beispiel auf der nächsten Seite erläutert nur das Ergebnis.
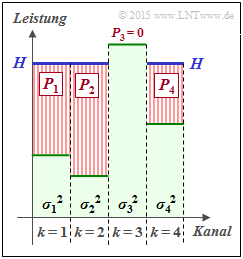Wir betrachten K = 4 parallele Gaußkanäle mit unterschiedlichen Störleistungen ( σ_1^2, ... , σ_4^2 ) gemäß der nebenstehenden Abbildung. Gesucht ist die bestmögliche Aufteilung der Sendeleistung auf die vier Kanäle.
Würde man dieses Profil langsam mit Wasser auffüllen, so würde das Wasser zunächst nur in den Kanal 2 fließen. Gießt man weiter, so sammelt sich auch im Kanal 1 etwas Wasser an und später auch im Kanal 4.
Die eingezeichnete „Wasserhöhe” H beschreibt genau den Zeitpunkt, zu dem die Summe (P_1 + P_2 + P_4) der insgesamt zur Verfügung stehenden Sendeleistung P_X entspricht.
Die optimale Leistungsaufteilung für dieses Beispiel ergibt P_2 > P_1 > P_4 sowie P_3 = 0. Erst bei größerer Sendeleistung P_X würde auch dem dritten Kanal eine kleine Leistung P_3 zugewiesen.
Man bezeichnet dieses Allokationsverfahren als Water–Filling–Algorithmus.
Werden alle K Gaußkanäle in gleicher Weise gestört ⇒ σ_1^2 = ... = σ_K^2 = P_N, so sollte man natürlich die gesamte zur Verfügung stehende Sendeleistung P_X gleichmäßig auf alle Kanäle verteilen: P_k = P_X/K. Für die Gesamtkapazität erhält man dann:
C_{\rm Gesamt} = \frac{ K}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X}{K \cdot P_N}) \hspace{0.05cm}.
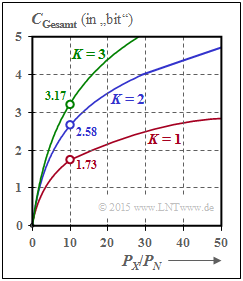
Die rechte Grafik zeigt die Gesamtkapazität als Funktion des Quotienten P_X/P_N für K = 1, K = 2 und K = 3.
- Bei P_X/P_N = 10 ⇒ 10 · \text{lg} (P_X/P_N) = 10 \text{dB} wird die Gesamtkapazität um ca. 50% größer, wenn man die Gesamtleistung auf zwei Kanäle gleichmäßig aufteilt.
- Im Grenzfall P_X/P_N → ∞ nimmt die Gesamtkapazität um den Faktor K zu ⇒ Verdoppelung mit K = 2.
Die beiden identischen und voneinander unabhängigen Kanäle kann man auf unterschiedliche Weise realisieren, zum Beispiel durch Zeit–, Frequenz– oder Raummultiplexverfahren. Der Fall K = 2 lässt sich aber auch durch die Verwendung orthogonaler Basisfunktionen wie „Cosinus” und „Sinus” verwirklichen wie zum Beispiel bei der Quadratur–Amplitudenmodulation (QAM) oder einer mehrstufigen Phasenmodulation wie QPSK oder 8–PSK.
