Exercise 3.13: Code Rate and Reliability
Das Kanalcodierungstheorem von Shannon besagt unter anderem, dass über einen Kanal mit beliebig kleiner Blockfehlerwahrscheinlichkeit übertragen werden kann, so lange die Coderate $R$ nicht größer ist als die Kanalkapazität $C$. Dieses Ergebnis erreicht man mit Kanalcodierung (englisch: Channel Coding) bei sehr großen Blocklängen: $n → ∞$, was mit einem beliebig großen Aufwand verbunden ist.
Diese Aussage basiert auf informationstheoretischen Gesetzmäßigkeiten, die Shannon selbst aufgestellt hat. Shannon sagt nicht, wie diese „unendlich gute” Kanalcodierung aussehen muss, er beweist nur, dass es sie gibt.
Der Umkehrschluss des Kanalcodierungstheorems sagt aus, dass mit einer Rate $R > C$ keine fehlerfreie Übertragung möglich ist. Es gibt kein Codiersystem mit verschwindend kleiner Fehlerwahrscheinlichkeit, auch wenn die Codierung noch so aufwändig und ausgeklügelt wäre.
Vielmehr lassen sich für den Fall $R > C$ zwei Schranken angeben:
- Überträgt man über einen diskreten gedächtnislosen Kanal (DMC) mit einer Rate $R$ größer als die Kanalkapazität $C$, so gibt es eine Schranke für die Bitfehlerwahrscheinlichkeit:
$$ p_{\rm B} \ge H_{\rm bin}^{-1} \left (1 - \frac{C}{R} \right) > 0 \hspace{0.05cm}.$$
- Soll die Bitfehlerwahrscheinlichkeit nach bestmöglicher Decodierung den Wert $p_B$ nicht überschreiten, so darf die Coderate einen vorgegebenen Grenzwert nicht unterschreiten:
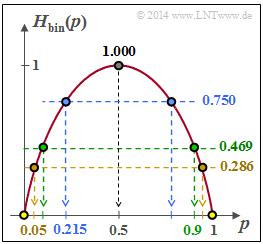
$$ R \le \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.05cm}.$$ In dieser Aufgabe sollen diese Gleichungen unter Verwendung der binären Entropiefunktion $$ H_{\rm bin}( p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$ numerisch ausgewertet werden. Diese ist oben skizziert. Wegen $0 < p_B ≤ 1$ und $0 < C/R < 1$ liegt das Argument der Funktion $H_{bin}(⋅)$ und deren Umkehrfunktion $H_{bin}^{ –1 }(⋅)$ stets zwischen $0$ und $1$. Hinweis: Die vorliegende Aufgabe behandelt einen Teilaspekt von Kapitel 3.3. Die Werte der binären Entropiefunktion werden zum Beispiel durch das folgende Flashmodul bereitgestellt:
Fragebogen
Musterlösung