Exercise 1.4Z: Representation of Oscillations

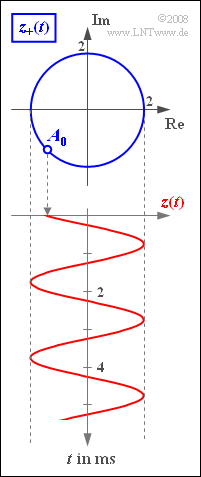
Betrachtet wird eine harmonische Schwingung $z(t)$, die zusammen mit dem zugehörigen Signal $z_+(t)$ in der Grafik dargestellt ist.

Diese Signale können mathematisch wie folgt beschrieben werden: $$z(t) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T}) \\ = A_{\rm T} \cdot \cos(2 \pi f_{\rm T}( t - \tau)) \hspace{0.05cm}, \\ z_+(t) = A_{\rm 0} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t}$$ Die zwei Amplitudenparameter $A_T$ und $A_0$ sind jeweils dimensionslos, der Phasenwert $ϕ_T$ soll zwischen $\text{±π}$ liegen und die Laufzeit τ ist nicht negativ.

Beachten Sie weiter, dass $ϕ_T$ in obiger Gleichung mit positivem Vorzeichen erscheint. Unter Anmerkungen zur Nomenklatur finden Sie eine Begründung für die unterschiedliche Verwendung von $φ_T$ und $ϕ_T = – φ_T$.

Die Teilaufgabe (d) bezieht sich auf das äquivalente TP–Signal $z_{TP}(t)$, das mit $z_+(t)$ in folgendem Zusammenhang steht: $$z_{\rm TP}(t) = z_+(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t} \hspace{0.05cm}.$$ Hinweis: Die Aufgabe bezieht sich auf das Kapitel 1.3 dieses Buches. Weitere Informationen zu dieser Thematik finden Sie in Kapitel 2.3 – Kapitel 4.2 – Kapitel 4.3 des Buches „Signaldarstellung” sowie bei den folgenden Interaktionsmodulen:

Zeigerdiagramm – Darstellung des analytischen Signals

Ortskurve – Verlauf des äquivalenten Tiefpass-Signals

Zu Kapitel 2.3: Anmerkung zur Nomenklatur der Phase Anzumerken ist, dass in diesem Tutorial – wie auch in anderer Literatur üblich – bei der Beschreibung von harmonischer Schwingung, Fourierreihe und Fourierintegral die Phase mit negativem Vorzeichen in die Gleichungen eingeht, während in Zusammenhang mit Modulationsverfahren die Phase stets mit einem Pluszeichen angesetzt wird. Zur Unterscheidung dieser beiden Varianten benutzen wir $φ$ und $ϕ$. Beide Symbole kennzeichnen das kleine griechische „phi”, wobei die Schreibweise $φ$ vorwiegend im deutschen und $ϕ$ im anglo-amerikanischen Sprachraum angewandt wird.

Die Phasenwerte $φ = 90°$ und $ϕ = –90°$ sind somit äquivalent und stehen beide für die Sinusfunktion: $$cos(2\Pi f_0t - 90°) = cos(2\Pi f_0t- \varphi) = cos(2\Pi f_0t + \phi) = sin(2\Pi f_0 t)$$

Fragebogen

$A_T$ =

$f_T$=

$\text{Hz}$

$\omega_T$ =

$\text{Hz}$

$ϕ_T$ =

$\text{Grad}$

$τ$ =

$\text{ms}$

$t_1$ =

$\text{ms}$

$Re[z_{TP}(t = 1 ms)]$ =

$Im[z_{TP}(t = 1 ms)]$ =

	Das Spektrum $Z(f)$ besteht aus zwei Diracfunktionen bei $±f_T$.
	Das Spektrum $Z_+(f)$ weist eine Diracfunktion bei $–f_T$ auf.
	Das Spektrum $Z_{TP}(f)$ beinhaltet eine Diracfunktion bei f = 0.
	Das analytische Signal $z_+(t)$ ist stets komplex.
	Das äquivalente TP–Signal $z_{TP}(t)$ ist stets komplex.

Musterlösung

Solution

1.Aus der grafischen Darstellung der Zeitfunktion $z(t)$ erkennt man die (normierte) Amplitude $A_T = 2$ und die Periodendauer $T_0 = 2$ Millisekunden. Deshalb ist die Signalfrequenz $f_T = 1/T_0 = 500 Hz$ und die Kreisfrequenz beträgt $ω_T = 2πf_T = 3141.5 1/s$.

2.Das analytische Signal lautet allgemein: $$z_+(t) = A_{\rm T} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}(\omega_{\rm T}\cdot \hspace{0.05cm}t + \phi_{\rm T})} = A_{\rm T} \cdot {\rm e}^{{\rm j} \cdot \phi_{\rm T}} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t }\hspace{0.05cm}.$$ Gleichzeitig gilt der Zusammenhang: $$A_0 = z_+(t = 0) = A_{\rm T} \cdot {\rm e}^{{\rm j} \cdot \phi_{\rm T}} \hspace{0.05cm}.$$ Die komplexe Amplitude $A_0$ kann aus der oberen Grafik abgelesen werden. $$A_0 = - \sqrt{2} - {\rm j} \cdot \sqrt{2} = A_{\rm 0} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} 0.75 \pi} \hspace{0.05cm}.$$ Ein Vergleich beider Gleichungen führt zum Ergebnis: $$ \phi_{\rm T} = - 0.75 \pi \hspace{0.15cm}\underline {= - 135^{\circ}} \hspace{0.05cm}.$$ Dabei besteht folgender Zusammenhang mit der Laufzeit $τ$: $$\phi_{\rm T} = - 2 \pi \cdot f_{\rm T} \cdot \tau \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \tau = \frac{-\phi_{\rm T}}{2 \pi \cdot f_{\rm T}} = \frac{0.75 \pi}{2 \pi \cdot 0.5\,{\rm kHz}} \hspace{0.15cm}\underline {= 0.75 \,{\rm ms}} \hspace{0.05cm}.$$

3.Das analytische Signal legt in der Zeit $T_0$ genau eine Umdrehung zurück. Ausgehend von $A_0$ erreicht man somit nach $T_0/8 = 0.25 ms$ zum ersten Mal, dass das analytische Signal imaginär ist: $z_+(t1) = – 2 j$. Wegen der Beziehung $z(t) = Re[z_+(t)]$ tritt zu diesem Zeitpunkt $t_1$ auch der erste Nulldurchgang des Signals $z(t)$ auf.

4.Mit dem Ergebnis aus b) erhält man: $$ z_{\rm TP}(t) = z_+(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t} = A_0 = A_{\rm T} \cdot {\rm e}^{{\rm j} \cdot \phi_{\rm T}} = {\rm const.}$$ Somit gilt für alle Zeiten t und damit auch für t = 1 ms: $${\rm Re}[z_{\rm TP}(t)] = - \sqrt{2} \hspace{0.15cm}\underline {= -1.414} \hspace{0.05cm},\\ {\rm Im}[z_{\rm TP}(t)] = - \sqrt{2}\hspace{0.15cm}\underline {= -1.414} \hspace{0.05cm}.$$

5.Richtig sind die Aussagen 1, 3 und 4:

Die einzige Diracfunktion von $Z_+(f)$ liegt bei $f = f_T$ und nicht bei $–f_T$.
Das analytische Signal einer harmonischen Schwingung ist immer komplex.
Das äquivalente TP–Signal einer harmonischen Schwingung ist meistens komplex.

Ausnahme: $z(t) = ±A_T · cos(ω_T · t).$