Exercise 2.4: Frequency and Phase Offset

Betrachtet wird das Quellensignal $$q(t) = A_{\rm 1} \cdot \cos(2 \pi f_{\rm 1} t ) +A_{\rm 2} \cdot \sin(2 \pi f_{\rm 2} t )$$ mit den Signalparametern $$ A_1 = 2\,{\rm V}, \hspace{0.15cm}f_1 = 2\,{\rm kHz}, \hspace{0.15cm}$$ $$A_2 = 1\,{\rm V}, \hspace{0.15cm}f_2 = 5\,{\rm kHz}\hspace{0.05cm}.$$ Dieses Signal wird ZSB–amplitudenmoduliert.

Das modulierte Signal $s(t)$ besitzt somit Spektralanteile bei $±45 kHz$, $±48 kHz$, $±52 kHz$ und $±55 kHz$. Bekannt ist weiter, dass das sendeseitige Trägersignal einen sinusförmigen Verlauf hat ($ϕ_T = –90°$).

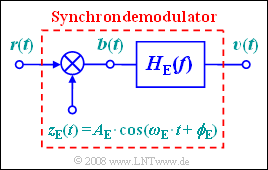
Die Demodulation soll mit nebenstehend skizzierter Schaltung erfolgen, die durch folgende Parameter bestimmt ist:

Amplitude $A_E$ (ohne Einheit),
Frequenz $f_E$,
Phase $ϕ_E$.

Der Block $H_E(f)$ beschreibt einen idealen, rechteckförmigen Tiefpass, der geeignet dimensioniert ist.

Hinweis: Diese Aufgabe gehört zum Themengebiet von Kapitel 2.2. Berücksichtigen Sie die folgenden trigonometrischen Umformungen: $$\\cos(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) + \cos(\alpha+\beta)\right] \hspace{0.05cm},$$ $$\\sin(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \left[ \sin(\alpha-\beta) + \sin(\alpha+\beta)\right] \hspace{0.05cm},$$ $$\\sin(\alpha)\cdot \sin(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) - \cos(\alpha+\beta)\right] \hspace{0.05cm}.$$

Fragebogen

	Der Demodulator würde bei ZSB–AM mit Träger besser arbeiten.
	Der Träger würde die Sendeleistung unnötigerweise vergrößern.
	Die richtige Dimensionierung des Tiefpasses $H_E(f)$ ist essentiell.
	Man könnte auch einen Hüllkurvendemodulator verwenden.
	Hüllkurvendemodulation ist nur für m < 1 anwendbar.

$A_E$ =

$f_F$ =

$\text{KHz}$

$\phi_E$

$ϕ_E = –120°: υ(t = 0)$ =

$\text{V}$

$ϕ_E = 0: υ(t = 0)$ =

$\text{V}$

	gilt $υ(t) = q(t) · cos(2π · Δf_T · t).$
	$υ(t)$ beinhaltet einen Spektralanteil bei 2 kHz.
	$υ(t)$ beinhaltet einen Spektralanteil bei 4 kHz.
	$υ(t)$ beinhaltet einen Spektralanteil bei 6 kHz.

Musterlösung

Solution

1.Richtig sind die Aussagen 2, 3 und 5: Bei ZSB–AM ohne Träger bzw. mit einem Modulationsgrad m > 1 ist Hüllkurvendemodulation nicht anwendbar. Die Leistungsfähigkeit des Synchrondemodulators wird durch den zusätzlichen Trägeranteil nicht gesteigert, sondern führt lediglich zu einer unnötigen Vergrößerung der aufzubringenden Sendeleistung.

Auch die dritte Aussage ist richtig. In der Musterlösung zu Z2.4 wird gezeigt, welche Auswirkungen ein Verzicht bzw. eine falsche Dimensionierung von $H_E(f)$ hat.

2.Wie der Name „Synchrondemodulator” bereits impliziert, müssen die Signale $z(t)$ und $z_E(t)$ frequenz– und phasensynchron sein: $$f_{\rm E} = f_{\rm T} \hspace{0.15cm}\underline {= 50\,{\rm kHz}}, \hspace{0.15cm}\phi_{\rm E} = \phi_{\rm T} \hspace{0.15cm}\underline {= - 90^{\circ}} \hspace{0.05cm}.$$ Die Trägerfrequenz $f_T$ kann dabei aus den Angaben über das Sendespektrum $S(f)$ ermittelt werden. Bei vollständiger Synchronität gilt: $$v(t) = \frac{A_{\rm E}}{2} \cdot q(t) + \frac{A_{\rm E}}{2} \cdot q(t)\cdot \cos(2 \cdot \omega_{\rm T} \cdot t ) \hspace{0.05cm}.$$ Der zweite Term wird durch den Tiefpass entfernt. Mit $A_E = 2$ gilt somit $υ(t) = q(t)$.

3. Im Theorieteil wurde gezeigt, dass bei ZSB–AM und Synchrondemodulation allgemein gilt: $$v(t) = \cos(\Delta \phi_{\rm T}) \cdot q(t) \hspace{0.05cm}.$$ Auch bei ungenügender Phasensynchronisation kommt es nicht zu Verzerrungen, sondern nur zu einer frequenzunabhängigen Dämpfung. Mit $ϕ_T = –90°$ und $ϕ_E = –120°$ ist $Δϕ_T = –30°$ und man erhält: $$ v(t) = \cos(30^{\circ}) \cdot q(t)= 0.866 \cdot q(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t= 0) = 0.866 \cdot A_1 \hspace{0.15cm}\underline {= 1.732\,{\rm V}}\hspace{0.05cm}.$$

4.Nun beträgt die Phasendifferenz $Δϕ_T = 90°$ und man erhält $υ(t) = 0$. Es ist müßig darüber zu diskutieren, ob es sich hierbei noch um ein verzerrungsfreies System handelt.

Das Ergebnis $υ(t) = 0$ ist darauf zurückzuführen, dass Cosinus und Sinus orthogonale Funktionen sind. Dieses Prinzip wird zum Beispiel bei der so genannten Quadratur–Amplitudenmodulation ausgenutzt.

5.Hier lautet die Gleichung für das Signal nach der Multiplikation: $$b(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t - 90^{\circ}) \cdot 2 \cdot \cos(\omega_{\rm E} \cdot t - 90^{\circ})=$$ $$ = 2 \cdot q(t) \cdot \sin(\omega_{\rm T} \cdot t ) \cdot \sin(\omega_{\rm E} \cdot t )\hspace{0.05cm}.$$ Dieses Ergebnis kann mit der trigonometrischen Umformung $$\sin(\alpha)\cdot \sin(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) - \cos(\alpha+\beta)\right]$$ auch wie folgt geschrieben werden: $$ b(t) = q(t) \cdot \cos((\omega_{\rm T} - \omega_{\rm E}) \cdot t ) + q(t) \cdot \cos((\omega_{\rm T} + \omega_{\rm E}) \cdot t ) \hspace{0.05cm}.$$ Der zweite Term liegt für $f_E ≈ f_T$ in der Umgebung von $2f_T$ und wird durch den Tiefpass entfernt. Somit bleibt mit der Frequenzdifferenz $Δf_T = f_E – f_T = 1 kHz$: $$ v(t) = q(t) \cdot \cos(2 \pi \cdot \Delta f_{\rm T} \cdot t) \hspace{0.05cm}.$$ Die erste Aussage ist somit richtig. Diese besagt, dass nun das Nachrichtensignal $υ(t)$ gemäß einer Cosinusfunktion leiser und wieder lauter wird („Schwebung”). Aus dem Cosinusanteil von $q(t)$ mit der Frequenz $f_1 = 2 kHz$ werden nun zwei Anteile (jeweils halber Amplitude) bei $1 kHz$ und $3 kHz$. Ebenso ist im Sinkensignal kein Anteil bei $f_2 = 5 kHz$ enthalten, sondern lediglich Anteile bei $4 kHz$ und $6 kHz$: $$1\,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t)\cdot \cos(2 \pi \cdot 1\,{\rm kHz} \cdot t) =$$ $$ 0.5\,{\rm V} \cdot \sin(2 \pi \cdot 4\,{\rm kHz} \cdot t)$$ $$+ 0.5\,{\rm V} \cdot \sin(2 \pi \cdot 6\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$ Richtig sind die Aussagen 1, 3 und 4.