Exercise 2.5: DSB-AM via a Gaussian channel
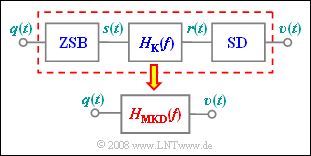
Das hier betrachtete Übertragungssystem setzt sich aus folgenden Blöcken zusammen:
- ZSB–AM ohne Träger mit $f_T = 50 kHz$ bzw. $f_T = 55 kHz$:
$$ s(t) = q(t) \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm} t).$$
- Gaußförmiger Bandpass–Kanalfrequenzgang:
$$H_{\rm K}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{|f| - f_{\rm M}}{\Delta f_{\rm K}}\right)^2} ,\hspace{0.2cm} f_{\rm M} = 50\,{\rm kHz},\hspace{0.2cm} \Delta f_{\rm K} = 10\,{\rm kHz}\hspace{0.05cm}.$$ Der Betrag $|f|$ im Exponenten berücksichtigt, dass $H_K(–f) = H_K(f)$ gilt.
- Synchrondemodulator mit optimalen Kenngrößen, so dass das Sinkensignal $υ(t)$ vollständig mit dem Quellensignal $q(t)$ übereinstimmt, wenn $H_K(f) = 1$ ist.
Auf der Seite Einfluss linearer Kanalverzerrungen wurde gezeigt, dass das gesamte System durch den resultierenden Frequenzgang $$H_{\rm MKD}(f) = \frac{1}{2} \cdot \left[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\right]$$ ausreichend genau charakterisiert ist. Der Index steht hierbei für „Modulator–Kanal–Demodulator”.
Das Quellensignal q(t) setzt sich aus zwei Cosinus-Schwingungen zusammen: $$q(t) = 2\,{\rm V}\cdot \cos (2 \pi \cdot 1\,{\rm kHz} \cdot t)+ 3\,{\rm V}\cdot \cos (2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$ Hinweis: Diese Aufgabe bezieht sich auf den Lehrstoff von Kapitel 2.2.
Fragebogen
Musterlösung