Exercise 1.3: Calculating with Complex Numbers

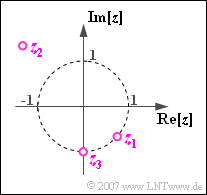
Nebenstehende Grafik zeigt einige Punkte in der komplexen Ebene, nämlich

$$z_1 = {\rm e}^{-{\rm j} 45^{ \circ}}, $$ $$z_2 = 2 \cdot{\rm e}^{{\rm j} 135^{ \circ}},$$ $$z_3 = -{\rm j} .$$

Im Verlauf dieser Aufgabe werden noch folgende komplexe Größen betrachtet: $$z_4 = z_2^2 + z_3^2,$$ $$z_5 = 1/z_2,$$ $$z_6 = \sqrt{z_3},$$ $$z_7 = {\rm e}^{z_2},$$ $$z_8 = {\rm e}^{z_2} + {\rm e}^{z_2^{\star}}.$$

Hinweise:

Die Aufgabe gehört zum Kapitel Zum_Rechnen_mit_komplexen_Zahlen.
Die Thematik wird auch im Lernvideo Rechnen mit komplexen Zahlen behandelt.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

	$2 \cdot z_1 + z_2 =0.$
	$z_1^{\ast} \cdot z_2 +2=0.$
	$(z_1/z_2) \cdot z_3$ ist rein reell.

$ x_4 = $

$ y_4 = $

$ x_5 = $

$ y_5 = $

$ \phi_6 ({\rm zwischen\hspace{0.1cm} 0^{\circ} \hspace{0.1cm}und \hspace{0.1cm} 180^{\circ} \hspace{0.1cm}Grad}) $ =

$\text{Grad}$

$ \phi_6 ({\rm zwischen\hspace{0.1cm} - \hspace{-0.15cm}180^{\circ} \hspace{0.1cm}und \hspace{0.1cm} 0^{\circ} \hspace{0.1cm}Grad}) $ =

$\text{Grad}$

$ x_7 = $

$ y_7 = $

$ x_8 = $

$ y_8 = $

Musterlösung

Solution

1. Entsprechend den Angaben gilt mit dem Signaldarstellung/Zum Rechnen mit komplexen Zahlen:

$2 \cdot z_1 + z_2 = 2 \cdot \cos(45^{ \circ}) - 2{\rm j}\cdot \sin(45^{ \circ})- 2 \cdot \cos(45^{ \circ}) + 2{\rm j} \cdot\sin(45^{ \circ}) = 0.$

Der zweite Vorschlag ist ebenfalls richtig, da

$z_1^{\star} \cdot z_2 = 1 \cdot{\rm e}^{{\rm j} 45^{ \circ}} \cdot 2 \cdot{\rm e}^{{\rm j} 135^{ \circ}} = 2 \cdot{\rm e}^{{\rm j} 180^{ \circ}}= -2.$

Dagegen ist der dritte Vorschlag falsch. Die Division von $z_1$ und $z_2$ liefert:

$\frac{z_1}{z_2} = \frac{{\rm e}^{-{\rm j} 45^{ \circ}}}{2 \cdot{\rm e}^{{\rm j} 135^{ \circ}}} = 0.5 \cdot{\rm e}^{-{\rm j} 180^{ \circ}}= -0.5.$

Die Multiplikation mit $z_3 = -{\rm j} $ führt zum Ergebnis j/2, also zu einer rein imaginären Größe. Richtig sind also die Lösungsvorschläge 1 und 2.

2. Das Quadrat von $z_2$ hat den Betrag $|z_2|^{2}$ und die Phase $2 \cdot \phi_2$:

$z_2^2 = 2^2 \cdot{\rm e}^{{\rm j} 270^{ \circ}}= 4 \cdot {\rm e}^{-{\rm j} 90^{ \circ}}=-4 \cdot {\rm j}.$

Entsprechend gilt für das Quadrat von $z_3$:

$z_3^2 = (-{\rm j})^2 = -1.$ Somit ist $x_4 = –1$ und $y_4 = –4.$

3. Durch Anwendung der Divisionsregel erhält man:

$z_5 = \frac{1}{z_2} = \frac{1}{2 \cdot e^{j135^{\circ}}} = 0.5 \cdot e^{-j135^{\circ}} = 0.5 \cdot (cos(-135^{\circ}) + j \cdot sin(-135^{\circ}))$ $\Rightarrow x_5 = y_5 = - \frac{\sqrt{2}}{4}= -0.354$

4. Die angegeben Beziehung für $z_6$ kann wie folgt umgeformt werden:

$z_6^2 = z_3 = e^{-90^{\circ}}$

Man erkennt, dass es zwei Möglichkeiten für $z_6$ gibt, die diese Gleichung erfüllen:

$z_6(1.Loesung) = \frac{z_2}{2}= 1 \cdot e^{j135^{\circ}} \Rightarrow \phi_6 = 135^{\circ}$

$z_6(2.Loesung) = z_1= 1 \cdot e^{-j45^{\circ}} \Rightarrow \phi_6 = -45^{\circ}$

5. Die komplexe Größe $z_2$ lautet in Realteil/imaginärteildarstellung:

$z_2 = x_2 + j \cdot y_2 = -\sqrt{2} + j \cdot \sqrt{2}$

Damit ergibt sich für die komplexe Exponentialfunktion\[z_7 = e^{-\sqrt{2}+j \cdot \sqrt{2}} = e^{-\sqrt{2}} \cdot (cos(\sqrt{2} + j \cdot sin(\sqrt{2})\]

Mit

$e^{-\sqrt{2}} = 0.243, \quad cos(\sqrt{2}) = 0.156, \quad sin(\sqrt{2}) = 0.988$

erhält man somit:

$z_7 = 0.243 \cdot (0.156 + j \cdot 0.988) = 0.038 + j \cdot 0.24$

6. Ausgehend vom Ergebnis 4. erhält man für $z_8$:

$z_8 = e^{-\sqrt{2}} \cdot (cos(\sqrt{2}) + j \cdot sin(\sqrt{2}) + cos(\sqrt{2}) - j \cdot (\sqrt{2}))$

$2 \cdot e^{-\sqrt{2}} \cdot cos(\sqrt{2}) = 2 \cdot x_7$

$\Rightarrow x_8 = 0.076, \quad y_8 =0$

	\(2 \cdot z_1 + z_2 =0.\)
	\(z_1^{\ast} \cdot z_2 +2=0.\)
	\((z_1/z_2) \cdot z_3\) ist rein reell.