Voraussetzungen und Definitionen
Wir betrachten in diesem Kapitel eine unendlich lange binäre Informationssequenz u und unterteilen diese in Informationsblöcke ui zu je k Bit. Man kann diesen Sachverhalt wie folgt formalisieren:
\[\underline{\it u} = \left ( \underline{\it u}_1, \underline{\it u}_2, ... \hspace{0.1cm}, \underline{\it u}_i , ... \hspace{0.1cm}\right ) \hspace{0.3cm}{\rm mit}\hspace{0.3cm} \underline{\it u}_i = \left ( u_i^{(1)}, u_i^{(2)}, ... \hspace{0.1cm}, u_i^{(k)}\right )\hspace{0.05cm},\]
\[u_i^{(j)}\in {\rm GF(2)}\hspace{0.3cm}{\rm f\ddot{u}r} \hspace{0.3cm}1 \le j \le k \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \underline{\it u}_i \in {\rm GF}(2^k)\hspace{0.05cm}.\]
Im Englischen bezeichnet man eine solche Sequenz ohne negative Indizes als semi–infinite.
\[\underline{\it x}_i = \left ( x_i^{(1)}, x_i^{(2)}, ... \hspace{0.1cm}, x_i^{(n)}\right )\in {\rm GF}(2^n)\hspace{0.05cm}.\]
Dieses ergibt sich entsprechend
- den k Bit des aktuellen Informationsblockes ui, und
- den m vorherigen Informationsblöcken u i–1, ... , u i–m.
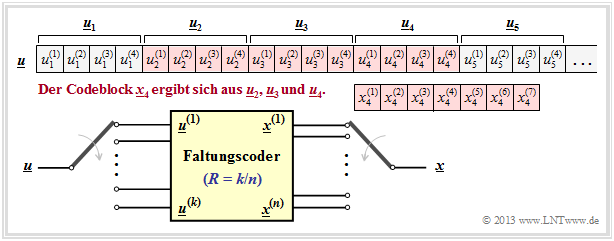
Die folgende Grafik verdeutlicht diesen Sachverhalt für die Parameter k = 4, n = 7, m = 2 und i = 4. Die n = 7 zum Zeitpunkt i = 4 erzeugten Codebits x4(1), ... , x4(7) können (direkt) von den k · (m + 1) = 12 rot markierten Informationsbits abhängen und werden durch Modulo–2–Additionen erzeugt.
Gelb eingezeichnet ist zudem ein (n, k)–Faltungscodierer. Zu beachten ist, dass sich der Vektor ui und die Sequenz u(i) grundlegend unterscheiden. Während ui = (ui(1), ui(2), ... , ui(k)) die k zum Zeitpunkt i parallel anliegenden Informationsbits zusammenfasst, bezeichnet u(i) = (u1(i), u2(i), ...) die (horizontale) Sequenz am i–ten Eingang des Faltungscodierers. Für den Faltungscode gelten folgende Definitionen:
- Die Coderrate ergibt sich wie bei den Blockcodes zu R = k/n.
- Man bezeichnet m als das Gedächtnis (englisch: Memory) des Codes und den Convolutional Code selbst mit CC(n, k, m).
- Daraus ergibt sich die Einflusslänge (englisch: Constraint Length) zu ν = m + 1.
- Für k > 1 gibt man diese Parameter oft auch in Bit an: mBit = m · k bzw. νBit = (m + 1) · k.