Exercise 2.3Z: Oscillation Parameters

• Return to book

Jede harmonische Schwingung kann auch in der Form

$$x(t)=C\cdot\cos\bigg(2\pi \cdot \frac{t-\tau}{T_0}\bigg)$$

geschrieben werden. Die Schwingung ist somit durch drei Parameter vollständig bestimmt:

• die Amplitude $C$,

• die Periodendauer $T_0$,

• die Verschiebung $\tau$ gegenüber einem Cosinussignal.

Eine zweite Darstellungsform lautet mit der Grundfrequenz $f_0$ und der Phase $\varphi$:

$$x(t)=C \cdot\cos(2\pi f_0t-\varphi).$$

Von einer harmonischen Schwingung ist nun bekannt, dass

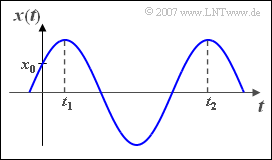
• das erste Signalmaximum bei $t_1 = 2 \text{ms}$ auftritt,

• das zweite Signalmaximum bei $t_2 = 14 \text{ms}$ auftritt,

• der Wert $x_0 = \text{x(t = 0)} = 3 \text{V}$ ist.

Hinweis: Diese Aufgabe bezieht sich auf das Kapitel 2.3.

Fragebogen

1

Wie groß ist die Periodendauer T0 und die Grundfrequenz f0?

$T_0$ = $\text{ms}$

$f_0$ = $\text{Hz}$

2

Welchen Wert haben hier die Verschiebung $\tau$ und die Phase $\varphi$ (in $\text{Grad}$)?

$\tau$ = $\text{ms}$

$\varphi$ = $\text{Grad}$

3

Wie groß ist die Amplitude der harmonischen Schwingung?

$\text{C}$ = $\text{V}$

4

Wie lautet das Spektrum? Welches Gewicht hat die Spektrallinie bei $+f_0$?

$\text{Re}[X(f = f_0)]$ = $\text{V}$

$\text{Im}[X(f = f_0)]$ = $-$ $\text{V}$

Musterlösung

Solution

1. Es gilt $T_0 = t_2 – t_1 = 12 \text{ms}$ und $f_0 = 1/T_0 \underline{\approx 83.33 \text{Hz}}$.

2. Die Verschiebung beträgt $\tau = 2 \text{ms}$; die Phase ist $\varphi = 2\pi \cdot \tau/T_0 = \pi/3$ entsprechend $60°$.

3. Aus dem Wert zum Zeitpunkt $t = 0$ folgt für die Amplitude $\text{C} = 6 \text{V}$:

$$x_0=x(t=0)=C\cdot\cos(-60\,^\circ)=\frac{C}{2}=\rm 3\,V \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm}\hspace{0.15cm}\underline{\it C=\rm 6\,V}.$$

4. Die dazugehörige Spektralfunktion lautet:

$$X(f)=\frac{C}{2}\cdot{\rm e}^{-{\rm j}\varphi}\cdot\delta(f-f_0)+\frac{C}{2}\cdot{\rm e}^{{\rm j}\varphi}\cdot\delta(f+f_0).$$

Das Gewicht der Diraclinie bei $f = f_0$ (erster Term) ist $\text{C}/2 \cdot e^{–\text{j}\varphi} \approx \underline{1.5 \text{V} – \text{j} \cdot 2.6 \text{V}}$.