Exercise 3.6: Even and Odd Time Signals

• Return to book

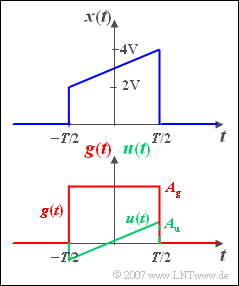
Gesucht ist das Spektrum $X(f)$ des nebenstehend skizzierten impulsförmigen Signals $x(t)$, das im Bereich von $–T/2$ bis $+T/2$ linear von $2\,\text{ V}$ auf $4\,\text{ V}$ ansteigt und außerhalb $0$ ist.

Die Spektralfunktionen der unten dargestellten Signale $g(t)$ und $u(t)$ werden als bekannt vorausgesetzt:

• Die gerade, rechteckförmige Zeitfunktion $g(t)$ besitzt das Spektrum

$$G( f ) = A_g \cdot T \cdot {\mathop{\rm si}\nolimits}( { {\rm{\pi }}fT} ) \hspace{0.3cm} {\rm{mit}}\hspace{0.3cm} {\mathop{\rm si}\nolimits}( x ) = \frac{ {\sin ( x )}}{x}.$$

• Das Spektrum der unsymmetrischen Funktion $u(t)$ lautet:

$$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\left[ {{\mathop{\rm si}\nolimits} ( { {\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \right].$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Gesetzmäßigkeiten der Fouriertransformation.
• Alle dort dargelegten Gesetzmäßigkeiten werden im Lernvideo Gesetzmäßigkeiten der Fouriertransformation (Dauer Teil 1: 5:57 – Teil 2: 5:55) an Beispielen verdeutlicht.
• Zwischen ${x(t)}$ und ${y(t)}$ besteht folgender Zusammenhang:

$$y( t ) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )}\, {\rm d}\tau .$$

• Der Integrationssatz lautet in entsprechend angepasster Form:

$$\frac{1}{T}\cdot \hspace{-0.1cm} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )}\,\, {\rm d}\tau\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f ) \cdot \left( {\frac{1}{{{\rm{j}}2{\rm{\pi }}fT}} + \frac{1}{2T}\cdot {\rm \delta} ( f )} \right).$$

• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.Verwenden Sie für die Teilaufgaben 1) und 2) die Signalparameter Au = 1 V und T = 1 ms.

Hinweis: Lösen Sie diese Aufgabe mit Hilfe des Zuordnungssatzes in Kapitel 3.3.

Fragebogen

1

Berechnen Sie die (rein imaginären) Spektralwerte des unsymmetrischen Signals $u(t)$ bei den Frequenzen $f$ = 0.5 kHz und $f$ = 1 kHz.

$Im[U(f=0.5 \text{kHz})] =$ mV/Hz

$Im[U(f=1 \text{kHz})] =$ mV/Hz

2

Wie groß ist der Spektralwert von $u(t)$ bei der Frequenz $f$ = 0? Hinweis: Lieber denken als rechnen.

$Im[U(f=0 \text{kHz})] =$ mV/Hz

3

Berechnen Sie unter Verwendung des Ergebnisses aus 1) den Spektralwert des Signals $x(t)$ bei der Frequenz $f$ = 0.5 kHz.

$Re[X(f=0.5 \text{kHz})] =$ mV/Hz

$Im[X(f=0.5 \text{kHz})] =$ mV/Hz

Musterlösung

Solution

1. Für $f \cdot T$ = 0.5 erhält man aus der angegebenen Gleichung:

$$U( {f = 0.5\;{\rm{kHz}}} ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {\rm{\pi }}} \cdot {\mathop{\rm si}\nolimits} ( {\frac{ {\rm{\pi }}}{2}} ) = - {\rm{j}} \cdot \frac{2}{ { {\rm{\pi }}^{\rm{2}} }} \cdot A_{\rm u} \cdot T.$$

Der Imaginärteil ist zahlenmäßig ca. $–2 \cdot 10^{–4}$ V/Hz. Dagegen liefert die si-Funktion bei $f \cdot T = 1$ den Wert 0, während der Cosinus gleich –1 ist. Damit erhält man mit $A_u$ = 1 V und $T$ = 1 ms:

$$U( {f = 1\;{\rm{kHz}}} ) = {\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{ { {\rm{2\pi }}}} \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm} {\rm Re} [...] \hspace{0.15 cm}\underline{ = 0}, \hspace{0.3 cm}{\rm Im} [...] \hspace{0.15 cm}\underline{\approx \cdot 1.59 \cdot 10^{ - 4} \;{\rm{V/Hz}}}.$$

2. Eine ungerade Zeitfunktion $u(t)$ besitzt nach dem Zuordnungssatz stets ein imaginäres und gleichzeitig ungerades Spektrum:

$$U( { - f} ) = - U( f ).$$

Mit dem Grenzübergang $f$ → 0 folgt aus der angegebenen Gleichung

$$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\left[ { {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \right]$$

das Ergebnis $U(f = 0)$. Formal könnte man dieses Ergebnis durch Anwendung der l'Hospitalschen Regel bestätigen. Wir gehen etwas pragmatischer vor. Setzen wir zum Beispiel $f \cdot T$ = 0.01, so erhält man:

$$\begin{align*} U( {f \cdot T = 0.01}) &= -{\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}( {{\mathop{\rm si}\nolimits} ( {0.01{\rm{\pi }}} ) - \cos ( {0.01{\rm{\pi }}} )} ) \\&= - {\rm{j}} \cdot \frac{ {A{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}( {0.999836 - 0.999507} ) \approx - {\rm{j}} \cdot 5 \cdot 10^{ - 6} \;{\rm{V/Hz}}{\rm{.}}\end{align*}$$

Für noch kleinere Frequenzwerte wird auch das Ergebnis immer kleiner. Schneller kommt man zum Ergebnis $U(f = 0) = 0$, wenn man berücksichtigt, dass das Integral über $u(t)$ verschwindet.

3. Das Signal $x(t)$ kann in einen geraden und einen ungeraden Anteil aufgeteilt werden, die zum geraden Realteil bzw. zum ungeraden Imaginärteil von $X(f)$ führen. Der gerade Anteil ist gleich der Funktion $g(t)$ mit $A_g$ = 3 V. Daraus folgt für den Spektralwert bei $f \cdot T$ = 0.5:

$${\mathop{\rm Re}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] = A_{\rm g} \cdot T \cdot {\mathop{\rm si}\nolimits} ( {\frac{ {\rm{\pi }}}{2}} ) \hspace{0.15 cm}\underline{= 1.91 \cdot 10^{ - 3} \;{\rm{V/Hz}}}{\rm{.}}$$

Der Imaginärteil ergibt sich aus der Spektralfunktion $U(f)$ mit $A_u$ = 1 V. Dieser wurde in der Teilaufgabe 1) berechnet:

$${\mathop{\rm Im}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] \hspace{0.15 cm}\underline{= - 2 \cdot 10^{ - 4} \;{\rm{V/Hz}}}{\rm{.}}$$