Contents
Einseitige Exponentialverteilung
Eine kontinuierliche Zufallsgröße $x$ nennt man (negativ-)exponentialverteilt, wenn sie nur nicht-negative Werte annehmen kann und die WDF für $x$ > 0 folgenden Verlauf hat: $$f_x(x)=\it \lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$
Das linke Bild zeigt die Wahrscheinlichkeitsdichtefunktion (WDF) einer exponentialverteilten Zufallsgröße $x$. Hervorzuheben ist:
- Definitionsgemäß gilt $f_{\rm x}(0) = λ/2.$
- Je größer der Verteilungsparameter $λ$ ist, um so steiler erfolgt der Abfall.
Für die Verteilungsfunktion (rechtes Bild) erhält man für $r$ > 0 durch Integration über die WDF: $$F_{\rm x}(r)=1-\rm e^{\it -\lambda\hspace{0.05cm}\cdot \hspace{0.03cm} r}.$$
Die Momente der Exponentialverteilung sind allgemein gleich $m_k = k!/λ^k.$ Daraus und aus dem Satz von Steiner ergibt sich für den Mittelwert und die Streuung: $$m_1=\frac{1}{\lambda},$$ $$\sigma=\sqrt{m_2-m_1^2}=\sqrt{\frac{2}{\lambda^2}-\frac{1}{\lambda^2}}=\frac{1}{\lambda}.$$
Die Exponentialverteilung hat große Bedeutung für Zuverlässigkeitsuntersuchungen, wobei in diesem Zusammenhang auch der Begriff Lebensdauerverteilung üblich ist. Bei diesen Anwendungen ist die Zufallsgröße oft die Zeit $t$, die bis zum Ausfall einer Komponente vergeht. Desweiteren ist anzumerken, dass die Exponentialverteilung eng mit der Poissonverteilung in Zusammenhang steht.
Transformation von Zufallsgrößen
Zur Erzeugung einer solchen exponentialverteilten Zufallsgröße an einem Digtalrechner kann zum Beispiel eine nichtlineare Transformation verwendet werden. Das zugrunde liegende Prinzip wird hier zunächst allgemein angegeben.
Besitzt eine kontinuierliche Zufallsgröße $u$ die WDF $f_{\rm u}(u)$, so gilt für die WDF der an der nichtlinearen Kennlinie $x = g(u)$ transformierten Zufallsgröße $x$: $$f_{\rm x}(x)=\frac{f_u(u)}{\mid g'(u)\mid}\Bigg |_{\hspace{0.1cm} u=h(x)}.$$
Hierbei bezeichnet $g'(u)$ die Ableitung der Kennlinie; $h(x)$ gibt die Umkehrfunktion zu $g(u)$ an.
Diese Gleichung gilt allerdings nur unter der Voraussetzung, dass die Ableitung $g'(u)$ ungleich 0 ist. Bei einer Kennlinie mit horizontalen Abschnitten $(g'(u) =$ 0) treten in der WDF zusätzliche Diracfunktionen auf, wenn die Eingangsgröße in diesem Bereich Anteile besitzt. Die Gewichte dieser Diracfunktionen sind gleich den Wahrscheinlichkeiten, dass die Eingangsgröße in diesen Bereichen liegt.
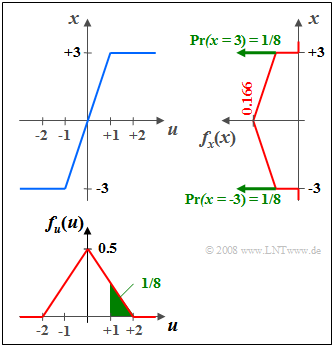Gibt man eine zwischen –2 und +2 dreieckverteilte Zufallsgröße $u$ auf eine Nichtlinerität mit der Kennlinie $x = g(u)$, die im Bereich $|u|$ ≤ 1 die Eingangswerte um den Faktor 3 verstärkt und alle Werte $|u|$ > 1 je nach Vorzeichen auf $x =$ ±3 abbildet, so ergibt sich die rechts skizzierte WDF $f_{\rm x}(x)$. Bitte beachten Sie:
- Aufgrund der Verstärkung um den Faktor 3 ist die WDF $f_{\rm x}(x)$ um diesen Faktor breiter und niedriger als $f_{\rm u}(u).$
- Die horizontalen Begrenzungen der Kennlinie bei $u =$ ±1 führen zu den beiden Diracfunktionen bei $x =$ ±3, jeweils mit Gewicht 1/8 ⇒ grüne Flächen in der WDF $f_{\rm u}(u).$
Erzeugung einer exponentialverteilten Zufallsgröße (1)
Es wird vorausgesetzt, dass die zu transformierende Zufallsgröße $u$ gleichverteilt zwischen 0 und 1 ist. Dann kann gezeigt werden, dass durch die monoton steigende Kennlinie $$x=\frac{1}{\lambda}\cdot \rm ln(\frac{1}{1-\it u})$$ eine einseitig exponentialverteilte Zufallsgröße $x$ mit folgender WDF entsteht: $$f_{\rm x}(x)=\lambda\cdot\rm e^{\it -\lambda x}\hspace{0.2cm}{\rm f\ddot{u}r}\hspace{0.2cm} {\it x}>0.$$
Für $x =$ 0 ist der WDF-Wert nur halb so groß. Negative $x$-Werte treten nicht auf, da für 0 ≤ $u$ < 1 das Argument der (natürlichen) Logarithmus–Funktion nicht kleiner wird als 1.
Die gleiche WDF erhält man übrigens mit der monoton fallenden Kennlinie $$x=\frac{1}{\lambda}\cdot \rm ln(\frac{1}{\it u})=-\frac{1}{\lambda}\cdot \rm ln(\it u \rm ).$$
Bei einer Rechnerimplementierung entsprechend der ersten Transformationskennlinie ist der Wert $u =$ 1 auszuschließen, im zweiten Fall der Wert $u =$ 0.
Zur Verdeutlichung der hier abgeleiteten Transformation bieten wir Ihnen ein Lernvideo an: Erzeugung einer Exponentialverteilung
In einem engen Zusammenhang mit der Exponentialverteilung steht die sogenannte Laplace- Verteilung mit der Wahrscheinlichkeitsdichtefunktion $$f_{\rm x}(x)=\frac{\lambda}{2}\cdot\rm e^{\it -\lambda \hspace{0.05cm} \cdot \hspace{0.05cm} | x|}.$$
Diese ist eine zweiseitige Exponentialverteilung, die insbesondere die Amplitudenverteilung von Sprach- und Musiksignalen ausreichend gut approximiert. Zur Generierung verwendet man eine zwischen ±1 gleichverteilte Zufallsgröße $υ$ (0 ausgeschlossen) und die Transformationskennlinie $$x=\frac{{\rm sign}(v)}{\lambda}\cdot \rm ln(\it v \rm ).$$
Mit dem folgenden Berechnungstool können Sie sich unter Anderem die Kenngrößen (WDF, VTF, Momente) der Exponential- und der Laplaceverteilung anzeigen lassen: WDF, VTF und Momente spezieller Verteilungen
Im zweiten Teil des unten aufgeführten Lernvideos wird an Beispielen gezeigt, dass die Laplace-Verteilung für die Beschreibung von Sprach- und Musiksignalen eine große Bedeutung besitzt: Wahrscheinlichkeit und Wahrscheinlichkeitsdichtefunktion (Dauer 6:30)
Erzeugung einer exponentialverteilten Zufallsgröße (2)
Ausführliche Herleitung der Transformationskennlinie
Es soll eine geeignete Transformationskennlinie $x = g(u)$ ermittelt werden, die aus einer zwischen 0 und 1 gleichverteilten Zufallsgröße $u$ eine einseitig exponentialverteilte Zufallsgröße $x$ formt: $$f_{\rm u}(u)= \left\{ \begin{array}{*{2}{c}} 1 & \rm falls\hspace{0.3cm} 0 < {\it u} < 1,\\ 0.5 & \rm falls\hspace{0.3cm} {\it u} = 0, {\it u} = 1,\\ 0 & \rm sonst, \\ \end{array} \right.$$ $$ f_{\rm x}(x)= \left\{ \begin{array}{*{2}{c}} \lambda\cdot\rm e^{\it -\lambda x} & \rm falls\hspace{0.3cm} {\it x} > 1,\\ \lambda/2 & \rm falls\hspace{0.3cm} {\it x} = 0 ,\\ 0 & \rm falls\hspace{0.3cm} {\it x} < 1. \\ \end{array} \right.$$
Ausgehend von der allgemeinen Transformationsgleichung $$f_{\rm x}(x)=\frac{f_{\rm u}(u)}{\mid g'(u) \mid }\Bigg |_{\hspace{0.1cm} u=h(x)}$$ erhält man durch Umstellen und Einsetzen der gegebenen WDF $f_{\rm x}(x):$ $$\mid g'(u)\mid\hspace{0.1cm}=\frac{f_{\rm u}(u)}{f_{\rm x}(x)}\Bigg |_{\hspace{0.1cm} x=g(u)}= {1}/{\lambda} \cdot {\rm e}^{\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}g(u)}.$$ Hierbei gibt $x = g'(u)$ die Ableitung der Kennlinie an, die wir als monoton steigend voraussetzen. Mit dieser Annahme erhält man $|g'(u)| = g'(u) = dx/du$ und die Differentialgleichung $${\rm d}u = \lambda\ \cdot {\rm e}^{-\lambda x}\, {\rm d}x$$ mit der Lösung $$u = K - {\rm e}^{-\lambda x}.$$ Aus der Bedingung, dass die Eingangsgröße $u =$ 0 zum Ausgangswert $x =$ 0 führen soll, erhält man für die Konstante $K =$ 1 und damit $$u = 1- {\rm e}^{-\lambda x}.$$ Löst man diese Gleichung nach $x$ auf, so ergibt sich die vorne angegebene Gleichung: $$x = \frac{1}{\lambda} \cdot {\rm ln} \left(\frac{1}{1 - u} \right) .$$ Bei einer Rechnerimplementierung ist allerdings sicherzustellen, dass für die gleichverteilte Eingangsgröße $u$ der kritische Wert 1 ausgeschlossen wird. Dies wirkt sich jedoch auf das Endergebnis nicht aus.
q.e.d.
