Exercise 4.2: Triangle Area again

• Return to book

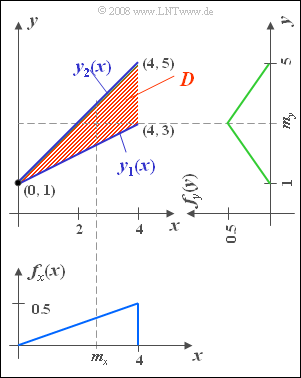
Wir betrachten die gleiche Zufallsgröße (x, y) wie in Aufgabe A4.1. In einem durch die Eckpunkte (0,1), (4,3) und (4,5) definierten dreieckförmigen Gebiet D sei die 2D–WDF f_xy(x, y) = 0.25. Außerhalb dieses Definitionsgebietes D (in der Grafik rot markiert) gibt es keine Werte.

Weiterhin sind im nebenstehenden Bild die beiden Randwahrscheinlichkeitsdichten bezüglich den Größen x und y eingezeichnet, die bereits in der Aufgabe A4.1 ermittelt wurden. Daraus lassen sich mit den Gleichungen von Kapitel 3.3 die Kenngrößen der beiden Zufallsgrößen bestimmen:

$$m_x=\rm 8/3 ,\hspace{0.5cm} \sigma_x=\rm \sqrt{8/9},$$

$$ m_y=\rm 3,\hspace{0.95cm} \sigma_y = \sqrt{\rm 2/3}.$$

Aufgrund der Tatsache, dass das Definitionsgebiet D durch zwei Gerade y₁(x) und y₂(x) begrenzt ist, kann hier das gemeinsame Moment erster Ordnung wie folgt berechnet werden.

$$m_{xy}=\rm E[\it x\cdot y]=\int\limits_{x_{\rm 1}}^{x_{\rm 2}}x\cdot \int\limits_{y_{\rm 1}(x)}^{y_{\rm 2}(x)}y \cdot f_{xy}(x,y) \, \,{\rm d}y\, {\rm d}x.$$

Hinweis: Diese Aufgabe bezieht sich auf den gesamten Inhalt von Kapitel 4.1.

Fragebogen

1

Wie lauten die Grenzgeraden des inneren Integrals zur m_xy-Berechnung?

	y1(x) = x + 1;      y2(x) = 2x + 1.
	y1(x) = x/2 + 1;   y2(x) = x + 1.
	y1(x) = x – 1;       y2(x) = 2x + 1.

2

Berechnen Sie das gemeinsame Moment m_xy gemäß dem Doppelintegral auf der Angabenseite. Hinweis: Setzen Sie x₁ = 0 und x₂ = 4.

$m_\text{xy}$ =

3

Welcher Wert ergibt sich für die Kovarianz?

$\mu_\text{xy}$ =

4

Wie groß ist der Korrelationskoeffizient?

$\rho_\text{xy}$ =

5

Wie lautet die Gleichung der Korrelationsgeraden y = K(x)? An welcher Stelle y₀ schneidet die Gerade die y-Achse? Zeigen Sie, dass die Korrelationsgerade auch durch den Punkt (m_x, m_y) geht.

$y_0$ =

Musterlösung

Solution

1.  Richtig ist der mittlere Vorschlag: Sowohl y₁(x) als auch y₂(x) schneiden die y-Achse bei y = 1. Die untere Begrenzungslinie hat die Steigung 0.5, die obere die Steigung 1.

2.  Entsprechend den Hinweisen erhalten wir:

$$m_{xy}=\int_{\rm 0}^{\rm 4}\it x \cdot \int_{\it x/\rm 2 +\rm 1}^{\it x+\rm 1}\rm \frac{1}{4}\cdot \it y \, \,{\rm d}y\,\, \, {\rm d}x = \rm\frac{1}{8}\cdot \int_{\rm 0}^{\rm 4}\it x\cdot[(\it x+\rm 1)^{\rm 2}- (\frac{\it x}{2}+\rm 1)^{\rm 2} ] \it \,\, {\rm d}x.$$

Dies führt zum Integral bzw. Endergebnis:

$$m_{xy}=\rm\frac{1}{8}\int_{\rm 0}^{\rm 4}(\rm\frac{3}{4}\it x^{\rm 3}+\it x^{\rm 2})\,{\rm d}x = \rm \frac{1}{8} \cdot (\frac{3}{16}\cdot 4^4+\rm \frac{4^3}{3})=\frac{26}{3}\hspace{0.15cm}\underline{ \approx 8.667}.$$

3.  Da beide Zufallsgrößen jeweils einen Mittelwert ungleich 0 besitzen, folgt für die Kovarianz:

$$\it \mu_{xy}=\it m_{xy}-m_{x}\cdot m_{y}=\frac{\rm 26}{\rm 3}-\frac{\rm 8}{\rm 3}\cdot\rm 3={2}/{3} \hspace{0.15cm}\underline{=0.667}.$$

4.  Mit den angegebenen Streuungen erhält man:

$$\rho_{xy}=\frac{\mu_{xy}}{\sigma_{x}\cdot\sigma_{y}}=\frac{{\rm 2}/{\rm 3}}{\sqrt{{\rm 8}/{\rm 9}}\cdot\sqrt{{\rm 2}/{\rm 3}}}=\sqrt{0.75}\hspace{0.15cm}\underline{=\rm 0.866}.$$

5.  Für die Korrelationsgerade gilt allgemein:

$$\it y-m_{y}=\rho_{xy}\cdot\frac{\sigma_{y}}{\sigma_ {x}}\cdot(x-m_{x}).$$

Mit den oben berechneten Zahlenwerten erhält man

$$y={\rm 3}/{\rm 4}\cdot \it x +\rm 1.$$

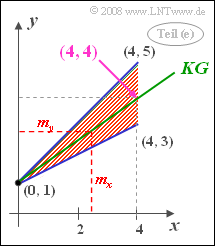
Die Korrelationsgerade schneidet die y-Achse bei y₀ = 1 und geht auch durch den Punkt (4, 4). Jedes andere Ergebnis wäre auch nicht zu interpretieren, wenn man das Definitionsgebiet betrachtet. Setzt man m_x = 8/3 ein, so erhält man y = m_y = 3. Das heißt: Die berechnete Korrelationsgerade geht tatsächlich durch den Punkt (m_x, m_y), wie es die Theorie besagt.