Exercise 4.1Z: Calculation of Moments

• Return to book

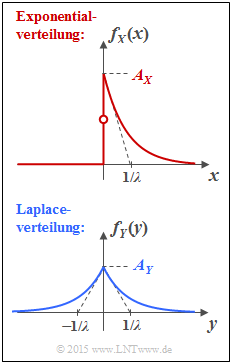
Die Grafik zeigt oben die Wahrscheinlichkeitsdichtefunktion (WDF) der Exponentialverteilung: $$f_X(x) = \left\{ \begin{array}{c} A_{ X} \cdot {\rm exp}(-\lambda \cdot x) \\ A_{ X}/2 \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm}x>0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x=0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x<0. \\ \end{array}$$ Darunter gezeichnet ist die WDF der Laplaceverteilung, die für alle y–Werte wie folgt angegeben werden kann: $$f_Y(y) = A_{ Y} \cdot {\rm exp}(-\lambda \cdot |y|)\hspace{0.05cm}.$$ Die zwei wertkontinuierlichen Zufallsgrößen X und Y sollen hinsichtlich der folgenden Kenngrößen verglichen werden:

• dem linearen Mittelwert m₁ (Moment erster Ordnung),
• dem Moment zweiter Ordnung  ⇒  m₂,
• der Varianz σ² = m₂ – m₁² (Satz von Steiner), und
• der Streuung σ.

Hinweis: Die Aufgabe gehört zum Kapitel 4.1 des vorliegenden Buches. Sie fasst gleichzeitig die erforderlichen Vorkenntnisse von Kapitel 3 des Buches „Stochastische Signaltheorie” zusammen. Gegeben sind außerdem die beiden unbestimmten Integrale: $$\int \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\hspace{0.05cm}, $$ $$\int \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot (\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) \hspace{0.05cm}. $$

Fragebogen

1

Wie groß ist der Maximalwert A_X der WDF f_X(x)?

	AX = λ/2,
	AX = λ,
	AX = 1/λ.

2

Wie groß ist der Maximalwert A_Y der WDF f_Y(y)?

	AY = λ/2,
	AY = λ,
	AY = 1/λ.

3

Gibt es ein Argument z, so dass f_X(z) = f_Y(z) gilt?

	Ja.
	Nein.

4

Welche Aussagen gelten für die Kenngrößen der Exponentialverteilung?

	Der lineare Mittelwert ist m1 = 1/λ.
	Der quadratische Mittelwert ist m2 = 2/λ2.
	Die Varianz ist σ2 = 1/λ2.

5

Welche Aussagen gelten für die Kenngrößen der Laplaceverteilung?

	Der lineare Mittelwert ist m1 = 1/λ.
	Der quadratische Mittelwert ist m2 = 2/λ2.
	Die Varianz ist σ2 = 1/λ2.

6

Mit welcher Wahrscheinlichkeiten unterscheidet sich die Zufallsgröße <nobr>(X bzw. Y)</nobr> vom Mittelwert m betragsmäßig um mehr als die Streuung σ?

$Exponential: Pr(|X – mX| > σX)$ =

$Laplace: Pr(|Y – mY| > σY)$ =

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.