Exercise 4.14Z: Echo Detection
From LNTwww
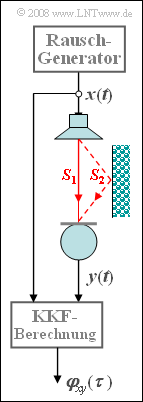
- Zur Messung akustischer Echos in Räumen – zum Beispiel bedingt durch Reflexionen an einer Wand – kann die nebenstehende Anordnung verwendet werden. Der Rauschgenerator erzeugt ein „im relevanten Frequenzbereich Weißes Rauschen” x(t) mit der Rauschleistungsdichte N0 = 10–6 W/Hz. Dieses ist bandbegrenzt auf Bx = 20 kHz und wird auf einen Lautsprecher gegeben. Die gesamte Messeinrichtung ist für den Widerstandswert R = 50 Ω ausgelegt.
- Das vom Mikrofon aufgenommene Signal ist im allgemeinsten Fall wie folgt beschreibbar:
- $$y(t) = \sum_{\mu = 1}^M \alpha_\mu \cdot x ( t - t_\mu ) .$$
- Hierbei bezeichnen αμ Dämpfungsfaktoren und tμ Laufzeiten.
- Bei dem hier gezeichneten Zweiwegemodell gilt M = 2: Zu dem direkten Pfad S1 kommt hier der Umweg S2 hinzu. Benutzen Sie für numerische Berechnungen die Parameterwerte
- $$\alpha_1 = 0.5, \hspace{0.2cm}t_1 = 200 \,{\rm ms}, \hspace{0.2cm}, \alpha_2 = 0.1, \hspace{0.2cm}t_2 = 250 \,{\rm ms}.$$
- Hinweis: Diese Aufgabe bezieht sich auf den Lehrstoff von Kapitel 4.6.
Fragebogen
Musterlösung
- 1. Das zweiseitige Leistungsdichtespektrum Φx(f) ist im Bereich von -Bx bis Bx konstant gleich N0/2. Dessen Fouriertransformierte ergibt die AKF:
- $$\varphi_x (\tau) = \frac{N_0}{2} \cdot 2 B_x \cdot {\rm si} (2 \pi B_x \tau) = 0.02 \hspace {0.05cm}{\rm W} \cdot {\rm si} (2 \pi B_x \tau).$$
- Umgerechnet von R = 50 Ω auf R = 1 Ω erhält man somit (Multiplikation mit R = 50 Ω):
- $$\varphi_x (\tau) = 0.02 \hspace {0.05cm}{\rm VA} \cdot 50 \hspace {0.05cm}{\rm V/A}\cdot {\rm si} (2 \pi B_x \tau)= 1 \hspace {0.05cm}{\rm V}^2 \cdot {\rm si} (2 \pi B_x \tau).$$
- Der Effektivwert ist die Wurzel aus dem AKF-Wert bei τ = 0:
- $$\sigma_x \hspace{0.15cm}\underline{= 1 \hspace {0.05cm}{\rm V}}.$$
- 2. Für die KKF gilt im vorliegenden Fall:
- $$\varphi_{xy} (\tau) = \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm}y(t+\tau)} = \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm}\left [ \alpha_1 \cdot x(t- t_1+ \tau)\hspace{0.1cm}+\hspace{0.1cm} \alpha_2 \cdot x(t- t_2+ \tau)\right] } . $$
- Nach Aufspaltung der Mittelwertbildung auf die beiden Terme erhält man hieraus:
- $$\varphi_{xy} (\tau) = \alpha_1 \cdot \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} x(t- t_1+ \tau)} \hspace{0.1cm}+\hspace{0.1cm} \alpha_2 \cdot \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} x(t- t_2+ \tau)} .$$
- Unter Verwendung der AKF kann hierfür auch geschrieben werden:
- $$\varphi_{xy} (\tau) = \alpha_1 \cdot {\varphi_{x}(\tau- t_1)} \hspace{0.1cm}+\hspace{0.1cm} \alpha_2\cdot {\varphi_{x}(\tau- t_2)} = \\ = 1 \hspace {0.05cm}{\rm V}^2 \cdot \left[ \alpha_1 \cdot {\rm si} (2 \pi B_x (\tau - t_1)) + \alpha_2 \cdot {\rm si} (2 \pi B_x (\tau - t_2)) \right].$$
- Die si-Funktion weist äquidistante Nulldurchgänge bei allen Vielfachen von 1/(2Bx) = 25 μs auf, jeweils bezogen auf deren Mittellagen bei t1 = 200 ms bzw. t2 = 250 ms.
- Daraus ergeben sich die KKF-Werte zu:
- $$\varphi_{xy} (\tau = 0) \hspace{0.15cm}\underline{= 0} ,$$
- $$\varphi_{xy} (\tau = t_1)= \alpha_1 \cdot \varphi_{x} (\tau = 0) \hspace{0.15cm}\underline{= 0.5\,{\rm V}^2} ,$$
- $$\varphi_{xy} (\tau = t_2)= \alpha_2 \cdot \varphi_{x} (\tau = 0) \hspace{0.15cm}\underline{= 0.1\,{\rm V}^2} .$$
- 3. Das Kreuzleistungsdichtespektrum ist die Fouriertransformierte der KKF, ebenso wie das LDS die Fouriertransformierte der AKF angibt. Mit den Ergebnissen aus 2) und 3) gilt deshalb:
- $${\it \Phi}_{xy} (f) = \alpha_1 \cdot {\it \Phi}_{x} (f) \cdot {\rm e}^{-{\rm j}2 \pi f t_1} \hspace{0.15cm}+ \hspace{0.15cm}\alpha_2 \cdot {\it \Phi}_{x} (f) \cdot {\rm e}^{-{\rm j}2 \pi f t_2}. $$
- Außerhalb des Bereichs |f| ≤ Bx ist das LDS Φx(f) - und dementsprechend auch das KLDS Φxy(f) - identisch 0. Innerhalb dieses Intervalls gilt Φx(f) = N0/2. Daraus folgt in diesem Bereich:
- $${\it \Phi}_{xy} (f) = \frac{N_0}{2} \left( \alpha_1 \cdot {\rm e}^{-{\rm j}2 \pi f t_1} \hspace{0.15cm}+ \hspace{0.15cm}\alpha_2 \cdot {\rm e}^{-{\rm j}2 \pi f t_2} \right). $$
- Es ist ersichtlich, dass Φxy(f) im Gegensatz zu Φx(f) eine komplexe Funktion ist. Bei f = 0 gilt:
- $${\it \Phi}_{xy} (f = 0) = \frac{N_0}{2} \left( \alpha_1 \hspace{0.15cm}+ \hspace{0.15cm}\alpha_2 \right) = 0.3 \cdot 10^{-6}\hspace{0.05cm}{\rm W/Hz} \hspace{0.15cm}\underline{= 15 \cdot 10^{-6}\hspace{0.07cm}{\rm V^2/Hz}} . $$
- 4. Die Fouriertransformierte einer diracförmigen AKF führt zu einem für alle Frequenzen f konstanten LDS, das heißt tatsächlich zu echt „Weißem Rauschen”. Dieses besitzt eine unendlich große Leistung, und für die KKF kann dann geschrieben werden:
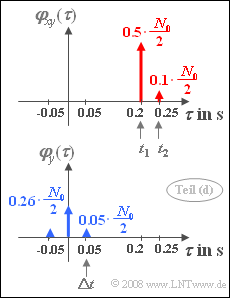
- $$\varphi_{xy} (\tau) = \frac{\alpha_1 N_0}{2} \cdot {\rm \delta}( \tau - t_1) \hspace {0.1cm}+ \hspace {0.1cm} \frac{\alpha_2 N_0}{2} \cdot {\rm \delta}( \tau - t_2) .$$
- Dieser Verlauf ist in der Grafik oben skizziert.
- Im Frequenzbereich ist für |f| ≤ Bx tatsächlich kein Unterschied gegenüber Teilaufgabe 3) feststellbar. Da nun aber echt weißes Rauschen vorliegt, ist hier im Gegensatz zu Punkt c) das KLDS nicht auf diesen Bereich beschränkt. Richtig sind demnach die Lösungsvorschläge 1 und 3.
- 5. Die AKF des echobehafteten Signals lautet wie folgt:
- $$\varphi_{y} (\tau) = \overline {y(t) \hspace{0.05cm}\cdot \hspace{0.05cm}y(t+\tau)} \\ = \alpha_1^2 \hspace{0.02cm}\cdot\hspace{0.02cm} \overline {x(t - t_1) \hspace{0.02cm}\cdot \hspace{0.02cm}x(t - t_1+ \tau)} \hspace{0.1cm} + \hspace{0.1cm} \alpha_1\hspace{0.02cm}\cdot \hspace{0.02cm}\alpha_2 \hspace{0.02cm}\cdot\hspace{0.02cm} \overline {x(t - t_1) \hspace{0.02cm}\cdot \hspace{0.02cm}x(t - t_2+ \tau)} \\ + \hspace{0.05cm} \alpha_2\hspace{0.02cm}\cdot \hspace{0.02cm}\alpha_1 \hspace{0.02cm}\cdot\hspace{0.02cm} \overline {x(t - t_2) \hspace{0.02cm}\cdot \hspace{0.02cm}x(t - t_1+ \tau)}\hspace{0.1cm} + \hspace{0.1cm}\alpha_2^2 \hspace{0.02cm}\cdot\hspace{0.02cm} \overline {x(t - t_2) \hspace{0.02cm}\cdot \hspace{0.02cm}x(t - t_2+ \tau)}. $$
- Für den ersten und den letzten Mittelwert gilt:
- $$\overline {x(t - t_1) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_1+ \tau)} = \overline {x(t - t_2) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_2+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + \tau)} =\varphi_x(\tau).$$
- Dagegen erhält man für den zweiten und den dritten Mittelwert mit Δt = t2 - t1 = 50 ms:
- $$\overline {x(t - t_1) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_2+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + t_1- t_2+ \tau)} =\varphi_x(\tau - \Delta t),$$
- $$\overline {x(t - t_2) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_1+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + t_2- t_1+ \tau)} =\varphi_x(\tau + \Delta t).$$
- Insgesamt ergibt sich somit wieder eine symmetrische AKF (siehe unteres Bild):
- $$\varphi_{y} (\tau) = \frac{N_0}{2} \cdot \left( ( \alpha_1^2 \hspace{0.1cm} + \hspace{0.1cm} \alpha_2^2 ) \cdot {\rm \delta} (\tau) \hspace{0.1cm} + \hspace{0.1cm} \alpha_1 \cdot \alpha_2 \cdot {\rm \delta}(\tau - \Delta t) \hspace{0.1cm} + \hspace{0.1cm} \alpha_1 \cdot \alpha_2 \cdot {\rm \delta}(\tau + \Delta t) \right).$$
- $$\Rightarrow \hspace{0.3cm}\varphi_{y} (\tau = 0 ) \hspace{0.15cm}\underline{= 13 \cdot 10^{-8}\, {\rm W/Hz}}, \hspace{0.3cm}\varphi_{y} (\tau = \Delta t )\hspace{0.15cm}\underline{ = 2.5 \cdot 10^{-8}\, {\rm W/Hz}}.$$